MZOJ #87 石子合并

 

分析

Part 1 模板题？

你说区间DP模板题？

恭喜你，TLE快乐

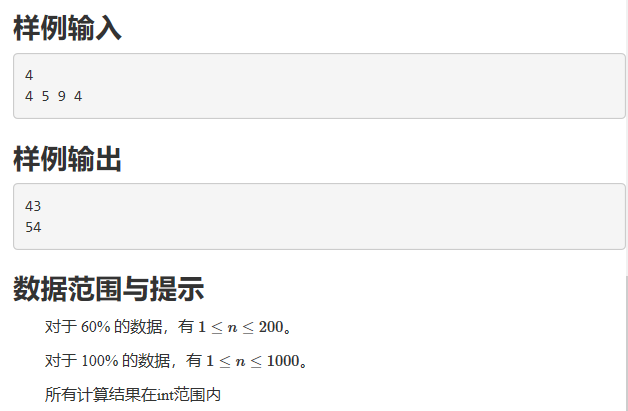
看到那个数据范围了吗？

Σ(っ°Д°;)っ

没错就是1000

你知道有一个东西叫做四边形优化么？

嗯，知道了就好

Part 2 真·分析

刚刚放的blog里有最小值的详解，就不再赘述了

不过值得注意的是这里最大值并不满足四边形优化

ᓫ(°⌑°)ǃ那怎么办

不急不急，我们看看这篇题解

看懂了么

听说这玩意还与哈夫曼树有关

每次选2堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。故最终得分就是每堆果子的重量乘以它参与合并的次数。这恰好就对应一个哈夫曼树问题，把果子看做叶子节点，建树，总得分就是叶子节点的权值乘以叶子的深度之和

对于区间（i,j），不管怎么合并，叶子节点权值都一样，故要最大化其深度，显然合并（i,j-1）或（i+1,j）深度最高。

代码

/***************************
User：Mandy
Language:c++
Problem:stone 
***************************/
#include<bits/stdc++.h>

using namespace std;

const int maxn = 2005;

int sum[maxn];
int fa[maxn][maxn],fi[maxn][maxn];
int s[maxn][maxn];

int n;

template<class T>inline void read(T &x){
    x = 0;char ch = getchar();bool flag = 0;
    while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
    if(flag) x = -x;
}

void readdata(){
    read(n);
    for(int i = 1;i <= n; ++ i){
        read(sum[i]);
        sum[i + n] = sum[i];
    }
    n <<= 1;n--; 
    for(int i = 1;i <= n; ++ i){
        sum[i] += sum[i - 1];
        s[i][i] = i;        
    }
}

void work(){
    for(int i = n;i >= 1; -- i)
        for(int j = i+1;j <= n; ++ j){
            int tmp = 0x3f3f3f3f;
            int id = 0;
            fa[i][j] = max(fa[i][j-1],fa[i+1][j]) + sum[j] - sum[i-1];
            for(int k = s[i][j-1];k <= s[i+1][j];++ k){
                int cur = fi[i][k] + fi[k+1][j] + sum[j] - sum[i-1];
                if(cur < tmp){
                    tmp = cur;
                    id = k;
                }
            }
            fi[i][j] = tmp;
            s[i][j] = id;
        }
        
    int ansmax = 0,ansmin = 0x3f3f3f3f;
    n=(n+1)>>1;
    for(int i = 1;i <= n; ++ i){
        ansmax = max(ansmax,fa[i][i+n-1]);
        ansmin = min(ansmin,fi[i][i+n-1]);
    }
    printf("%d\n%d",ansmin,ansmax);
}

int main(){
    readdata();
    work();
    return 0;
}