MZOJ #81 最小得分和



分析
1.不能再暴力的暴力(40)
最暴力的方法:将所有的差求出来然后排序,选出最小的k个
复杂度:O (N2logN)
2.比较不暴力的暴力(80)
还记得蚯蚓吗,决策单调
这道题其实也有隐藏的单调,甚至比蚯蚓还要明显的多
先将n个数排序,当然,离i越近,差越小,这是相对i而言的
不过蚯蚓哪里只要三个队列就好,这里,如果用那个方法,怕是要n个队列
这道题还是用堆吧,看下面hty的题解中的80分做法
机房里也有大佬这么做
首先将每相邻两个元素差值入堆,每次选取当前堆中最小的数,找到它在原序列中的位置i,然后向左找到第一个没有取的数对(i,p[i]),将堆顶元素变为s[i]-s[p[i]-1],s[i]为前缀和,然后dec(p[i]),做K次得到答案
复杂度:O(KlogN)
3.满分做法(100)
我考场上并没有想到80分的做法,直接由最暴力的做法得到了思路,于是写了正解……
然而我觉得80分的做法比正解要难想诶
我们先看看暴力:
最暴力的方法:将所有的差求出来然后排序,选出最小的k个
对于每一个差,我们都可以找到一个减数,一个被减数
为了简化问题,我们将n个数从小到大排序,以免不必要的枚举
我们可以发现,对于每一个被减数,一定是离他近的减数与他相减所得的差小
有了以上分析的单调性,我们再看,对于每一个差值,差值越大,那么小于等于它的差值就越多
废话
对,就是这个性质,给了我们二分的可能
我们所求的就是前k个最小的差不是吗,这k个差有上限,也就是第k大的差值
不如就二分这个上限,我们可以在O(n)的时间内求出这个上限所含的差值的个数:

求出了我们的上限,我们应该怎么算答案呢?
且看上面的程序,在求个数的时候,我们明显还维护了被减数的减数下限(也就是每一个i所对应的j)
a[i] 与a[j] ~ a[i-1]的差都小于等于第k大的差,都是要加到答案里的
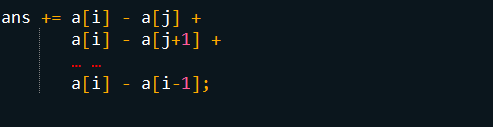
重新组合整理一下,就变成了这样:

这个,完全可以用前缀和优化呀
于是,最终版是这样的:

Over
不对,你以为就这样完了?
太天真了
WA快乐
我们求出了第k大的值,可谁说小于等于第k大的差值就一定有k个呢
Σ(っ°Д°;)っ
看这组数据,
4 5
1 1 2 3
我们求出的差值为
0 1 1 1 2 2
第5大的是2,但是2有两个,上述代码没有处理多余的2
所以,代码的最后需要减去多余的2
cnt是实际小于等于第k大的差值的个数,cur是第k大的差值的值

真的Over了
复杂度:O(NlogN+NlogaN)
4.题解 By hty(^v^)
题解当然要最后放……

代码

1 /******************** 2 User:Mandy 3 Language:c++ 4 Problem: 5 ********************/ 6 #include<bits/stdc++.h> 7 8 using namespace std; 9 10 typedef long long ll; 11 12 const int maxn = 1e6 + 5; 13 14 ll n,k; 15 ll a[maxn]; 16 ll sum[maxn]; 17 char *TT,*mo,but[(1 << 15) + 2]; 18 #define getchar() ((TT == mo && (mo = ((TT = but) + fread(but,1,1 << 15,stdin)),TT == mo)) ? -1 : *TT++) 19 template<class T>inline void read(T &x){ 20 x = 0;bool flag = 0;char ch = getchar(); 21 while(!isdigit(ch)) flag |= ch == '-',ch = getchar(); 22 while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar(); 23 if(flag) x = -x; 24 } 25 26 template<class T>void putch(const T x){ 27 if(x > 9) putch(x / 10); 28 putchar(x % 10 | 48); 29 } 30 31 template<class T>void put(const T x){ 32 if(x < 0) putchar('-'),putch(-x); 33 else putch(x); 34 } 35 36 void file(){ 37 freopen("mark.in","r",stdin); 38 freopen("mark.out","w",stdout); 39 } 40 41 void readdata(){ 42 read(n);read(k); 43 for(int i = 1;i <= n; ++ i) read(a[i]); 44 sort(a + 1,a + 1 + n); 45 } 46 47 bool check(ll x){ 48 ll j = 1,cnt = 0; 49 for(ll i = 2;i <= n; ++ i){//被减数 50 51 while(a[i] - a[j] > x)//减数 52 j++; 53 cnt += i - j; 54 if(cnt >= k) return 1; 55 } 56 return 0; 57 } 58 59 void work(){ 60 long long l = 0,r = a[n] - a[1],cur; 61 while(l <= r){//二分第k大的差 62 ll mid = (l + r) >> 1; 63 if(check(mid)) cur = mid,r = mid - 1; 64 else l = mid + 1; 65 } 66 ll j = 1; 67 for(int i = 1;i <= n; ++ i) sum[i] = sum[i - 1] + a[i]; 68 ll cnt = 0,ans = 0; 69 for(ll i = 2; i <= n ; ++ i){ 70 while(a[i] - a[j] > cur) j++; 71 ans = ans - (sum[i-1] - sum[j-1]) + a[i] * (i-j); 72 cnt += (long long)i-j; 73 } 74 if(cnt > k) ans -= cur * (cnt - k); 75 put(ans); 76 } 77 78 int main(){ 79 // file(); 80 readdata(); 81 work(); 82 return 0; 83 }



