luogu 2331 [SCOI2005]最大子矩阵

题目描述

这里有一个n*m的矩阵，请你选出其中k个子矩阵，使得这个k个子矩阵分值之和最大。注意：选出的k个子矩阵不能相互重叠。

输入格式

第一行为n,m,k（1≤n≤100,1≤m≤2,1≤k≤10），接下来n行描述矩阵每行中的每个元素的分值(每个元素的分值的绝对值不超过32767)。

输出格式

只有一行为k个子矩阵分值之和最大为多少。

输入输出样例

输入 #1复制

3 2 2
1 -3
2 3
-2 3

输出 #1复制

9

分析

方法1

O(n³*k)：luogu 2331 题解

这题中，空矩阵也算子矩阵

m == 1时dp[前i列][选了j个矩阵]，分为选与不选当前格两种，选的时候可以连着前面的当做一个矩阵

 

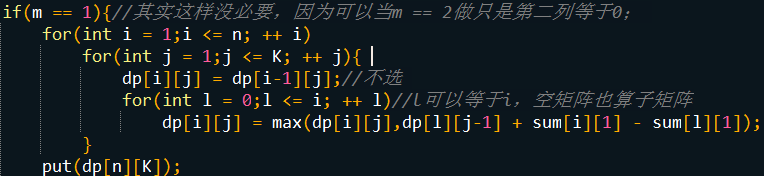
m == 2 的做法类比m == 1的做法，

f[第1列选了前i个][第2列选了前j个][选了k个子矩阵] = 最大和

对于当前的要选的子矩阵，选的情况有4种：

1. 不选

2. 选第一列

3.选第二列

3.i==j时两列可以看做一个矩阵

 

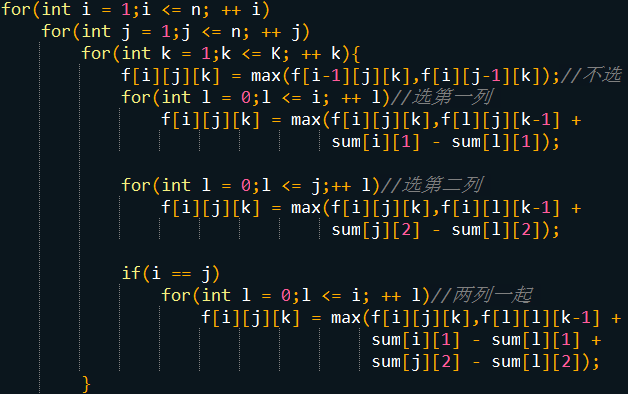
代码：

/***********************
User：Mandy.H.Y
Language:c++
Problem:
Algorithm: 
***********************/

#include<bits/stdc++.h>

using namespace std;

const int maxn = 105;

int n,m,K;
int a[105][5];
int sum[105][5];
int dp[maxn][15];
int f[maxn][maxn][15];

template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
    freopen("2331","r",stdin);
}

void readdata(){
    read(n);read(m);read(K);
    for(int i = 1;i <= n; ++ i){
        for(int j = 1;j <= m; ++ j){
            read(a[i][j]);
            sum[i][j] = sum[i - 1][j] + a[i][j];
        }
    }
}

void work(){
    if(m == 1){//其实这样没必要，因为可以当m == 2做只是第二列等于0； 
        for(int i = 1;i <= n; ++ i)
            for(int j = 1;j <= K; ++ j){ 
                dp[i][j] = dp[i-1][j];//不选 
                for(int l = 0;l <= i; ++ l)//l可以等于i，空矩阵也算子矩阵
                    dp[i][j] = max(dp[i][j],dp[l][j-1] + sum[i][1] - sum[l][1]);
            }
        put(dp[n][K]);
    } else {
        for(int i = 1;i <= n; ++ i)
            for(int j = 1;j <= n; ++ j)
                for(int k = 1;k <= K; ++ k){
                    f[i][j][k] = max(f[i-1][j][k],f[i][j-1][k]);//不选 
                    for(int l = 0;l <= i; ++ l)//选第一列 
                        f[i][j][k] = max(f[i][j][k],f[l][j][k-1] + 
                                         sum[i][1] - sum[l][1]);
                    
                    for(int l = 0;l <= j;++ l)//选第二列 
                        f[i][j][k] = max(f[i][j][k],f[i][l][k-1] + 
                                         sum[j][2] - sum[l][2]);
                    
                    if(i == j)
                        for(int l = 0;l <= i; ++ l)//两列一起 
                            f[i][j][k] = max(f[i][j][k],f[l][l][k-1] + 
                                             sum[i][1] - sum[l][1] + 
                                             sum[j][2] - sum[l][2]);
                }
        put(f[n][n][K]);
    } 
}

int main(){
//    file();
    readdata();
    work();
    return 0;
}