luogu 2569 [SCOI2010]股票交易

分析

显然的DP，就不多说了吧

推荐题解：题解 P2569 【[SCOI2010]股票交易】

 

Part 1 状态

涉及到的状态：天数，股票，买卖

转移的时候，应只与股票有关，是否买卖有一定关系，但可以从前一天转移

所以：dp[天数][这一天后所持股票数] = 最大收入

 

Part 2 初值

说实话，我发现边界与初值是很重要的一部分

看这道题，由于股票不可能凭空出现，需要购买，

所以不可能赋值为零，初值应该是持有这么多股票的买入价

求最大，还是赋极小值吧

 

Part 3 转移

少不得要分类讨论

初值是持有这么多股票的买入价，也就是空买（买入有上限）

而也可以选择不买不卖：

接下来考虑转移买卖；

首先，本身天数就少于w的不做考虑，会出现负下标

我们可以只考虑i - w - 1的情况

嗯？不是1~i - w - 1都可以吗?

你看这句话：

不是把前面的最优情况都考虑到了？

好吧，有点道理

考虑买卖的方程：

难道要多一维?

当然不可能

看限制，固定区间的最值，考虑考虑单调队列

稍微变个型：

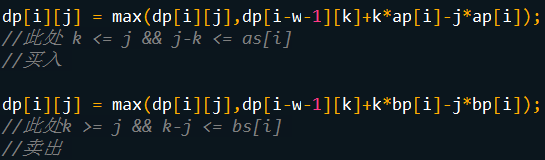
这样就好了，单调队列直接维护dp[i-w-1][k]+k*bp[i]就好

代码

 1 /************************
 2 User:Mandy.H.Y
 3 Language:c++
 4 Problem:luogu2569
 5 Algorithm:
 6 ************************/
 7 
 8 #include<bits/stdc++.h>
 9 
10 using namespace std;
11 
12 const int maxn = 2005;
13 
14 int t,maxp,w;
15 int dp[maxn][maxn];
16 int ap[maxn],bp[maxn],as[maxn],bs[maxn];
17 int q[maxn],l,r;
18 
19 template<class T>inline void read(T &x){
20     x = 0;bool flag = 0;char ch = getchar();
21     while( ! isdigit(ch)) flag |= ch == '-',ch = getchar();
22     while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
23     if(flag) x = -x;
24 }
25 
26 template<class T>void putch(const T x){
27     if(x > 9) putch(x / 10);
28     putchar(x % 10 | 48);
29 }
30 
31 template<class T>void put(const T x){
32     if(x < 0) putchar('-'),putch(-x);
33     else putch(x);
34 }
35 
36 void file(){
37     freopen("2569.in","r",stdin);
38     freopen("2569.out","w",stdout);
39 }
40 
41 void readdata(){
42     read(t);read(maxp);read(w);
43     for(int i = 1;i <= t; ++ i){
44         read(ap[i]);read(bp[i]);
45         read(as[i]);read(bs[i]);
46     }
47 }
48 
49 void work(){
50     memset(dp,128,sizeof(dp)); 
51     //注意初值与边界,不一定为0 
52     //赋为极小值，因为股票必须靠买，而不能直接为0； 
53     //不必为j = 0时赋零，因为j=0时 -1 * j * as[i] = 0 
54     for(int i = 1;i <= t ; ++ i){
55         
56         for(int j = 0;j <= maxp; ++ j){
57             if(j <= as[i]) dp[i][j] = -1 * j * ap[i];
58             dp[i][j] = max(dp[i][j],dp[i-1][j]);
59         }
60         
61         if(i <= w) continue;
62         //我们可以只考虑i - w - 1的情况
63         //dp[i][j] = max(dp[i][j],dp[i-1][j]);考虑到了之前的最优情况 
64         l = r = 0;
65         for(int j = 0;j <= maxp; ++ j){//买入 
66             while(l < r && j - q[l] > as[i]) l++;
67             while(l < r && dp[i-w-1][q[r-1]] + q[r-1] * ap[i] <= dp[i-w-1][j] + j * ap[i]) r--;
68             q[r++] = j;
69             if(l < r) dp[i][j] = max(dp[i][j],dp[i - w-1][q[l]] - (j - q[l]) * ap[i]);
70         } 
71         
72         l = r = 0;
73         for(int j = maxp;j >= 0; -- j){//卖出 
74             while(l < r && q[l] - j > bs[i]) l++;
75             while(l < r && dp[i-w-1][q[r-1]] + q[r-1] * bp[i] <= dp[i-w-1][j] + j * bp[i]) r--;
76             q[r++] = j;
77             if(l < r) dp[i][j] = max(dp[i][j],dp[i - w-1][q[l]] + (q[l] - j) * bp[i]);            
78         }
79     }
80     
81     put(dp[t][0]);
82     
83 }
84 
85 int main(){
86 //    file();
87     readdata();
88     work();
89     return 0;
90 }
View Code

 

posted @ 2019-09-05 08:55  Mandy_H_Y  阅读(138)  评论(0)  编辑  收藏  举报