luogu 1099 树网的核


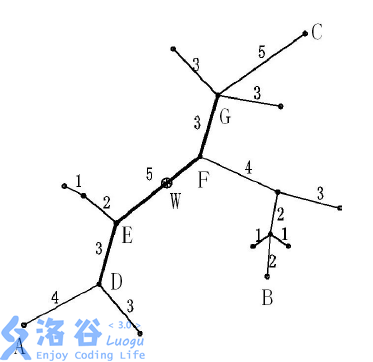

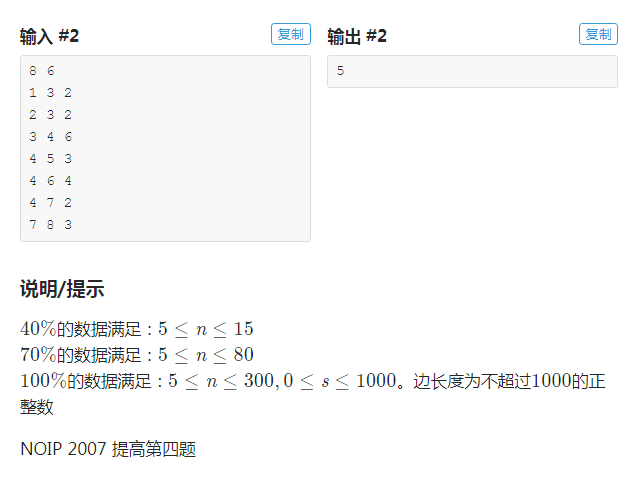
PS.图片来自luogu
分析
我发现CCF的题目都好长
part 1
一句话题意:
在树的直径上求一段连续的路径使得树上的点与这条路径的距离的最大值最小;
part 2
好的,最大值最小
少不得要考虑二分了
这个东西与任意两点间的最短路有关,看数据范围
Floyd没跑了
part 3
求树的直径有一个结论:
从树上任意一点找到最长路,再从最长路的另一端再跑一个最长路,这个最长路就是直径
反证法就好啊
这个要排在Floyd前面
part 4
题目所求为直径上的一段连续区间,也就是说直径的两端都是被删了的
这就好办了
暴力删边
暴力的想法是:
二分答案
枚举删边(左右各一次),把直径左右的删掉,剩下的片段就是与树上各点的距离不超过mid的
再判断这一段是否超过s
枚举删边的时候:

太暴力了,我都看不下去了
其实可以预处理出树上各点到直径的最短距离以及相应的直径上的点的编号
然后删边的时候加上与这个要删的点之间的距离就好(可以证明这就是最短的距离)
part 5
整理:
首先求出直径顺便按路径顺序存下直径上的点
Floyd求出树上任意两点间的距离
我们二分答案,注意左右边界
右边界表示不会大于直径的一半,但一半不一定在直径上(直接加一个最大边权就好)
左边界表示需要预处理
我们在处理出直径及其路径后,可以顺便求出树上各点到直径的最短距离以及相应的直径上的点的编号
其中,最大的那个距离就是左边界,需要左右边界与我的方法有关
代码

1 /********************** 2 User:Mandy.H.Y 3 Langauge:c++ 4 Problem:luogu 1099 5 Algorithm: 6 date:2019.9.3 7 **********************/ 8 9 #include<bits/stdc++.h> 10 11 using namespace std; 12 13 const int maxn = 305; 14 15 int n,s,start,mdis,end,cnt,mw; 16 int dia[maxn]; 17 bool vis[maxn]; 18 int g[maxn][maxn],dis[maxn],path[maxn],tmp[maxn]; 19 20 template<class T>inline void read(T &x){ 21 x = 0;char ch = getchar();bool flag = 0; 22 while(!isdigit(ch)) flag |= ch == '-',ch = getchar(); 23 while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar(); 24 if(flag) x = -x; 25 } 26 27 template<class T>void putch(const T x){ 28 if(x > 9) putch(x / 10); 29 putchar(x % 10 | 48); 30 } 31 32 template<class T>void put(const T x){ 33 if(x < 0) putchar('-'),putch(-x); 34 else putch(x); 35 } 36 37 void file(){ 38 freopen("testdata.in","r",stdin); 39 // freopen("1099.out","w",stdout); 40 } 41 42 void readdata(){ 43 read(n);read(s); 44 memset(g,0x3f3f3f3f,sizeof(g)); 45 for(int i = 1;i < n; ++ i){ 46 int u,v,w; 47 read(u);read(v);read(w); 48 g[u][v] = g[v][u] = w; 49 mw = max(mw,w); 50 } 51 for(int i = 1;i <= n; ++ i) g[i][i] = 0; 52 } 53 54 void Floyd(){ 55 for(int k = 1;k <= n; ++ k) 56 for(int i = 1;i <= n; ++ i) 57 for(int j = 1;j <= n; ++ j) 58 if(g[i][k] + g[j][k] < g[i][j]) 59 g[i][j] = g[j][i] = g[i][k] + g[j][k]; 60 61 } 62 63 void dfs1(int u){ 64 vis[u] = 1; 65 for(int i = 1;i <= n; ++ i){ 66 if(vis[i] || g[u][i] == 0x3f3f3f3f) continue; 67 dis[i] = dis[u] + g[u][i]; 68 if(dis[i] > mdis) { 69 start = i; 70 mdis = dis[i]; 71 } 72 dfs1(i); 73 } 74 } 75 76 void dfs2(int u){ 77 vis[u] = 1; 78 for(int i = 1;i <= n; ++ i){ 79 if(vis[i] || g[u][i] == 0x3f3f3f3f) continue; 80 dis[i] = dis[u] + g[u][i]; 81 path[i] = u; 82 if(dis[i] > mdis) { 83 end = i; 84 mdis = dis[i]; 85 } 86 dfs2(i); 87 } 88 } 89 90 bool check(int x){ 91 //--------删开头 92 start = 1;end = cnt; 93 int sum = mdis;//所取片段的长度 94 int i = 1; 95 bool judge = 0; 96 while(i < cnt){ 97 for(int j = 1;j <= n; ++ j){ 98 if(tmp[j] <= i) 99 if(dis[j] + g[dia[tmp[j]]][dia[i + 1]] > x){ 100 judge = 1;//%%%%%%%%%%%%%%% 101 break; 102 } 103 } 104 if(judge) break; 105 sum -= g[dia[i]][dia[i + 1]]; 106 start = i + 1; 107 ++i; 108 } 109 //---------删结尾 110 i = end; 111 judge = 0; 112 while(i > start){// > start 113 for(int j = 1;j <= n; ++ j){ 114 if(tmp[j] >= i) 115 if(dis[j] + g[dia[tmp[j]]][dia[i - 1]] > x){ 116 judge = 1; 117 break; 118 } 119 } 120 if(judge) break; 121 sum -= g[dia[i]][dia[i - 1]]; 122 end = i - 1; 123 --i; 124 } 125 //注意start与end都是在直径中的标号,不是真正编号 126 if(g[dia[start]][dia[end]] > s) return 0; 127 else return 1; 128 } 129 130 void work(){ 131 //--------------求直径 132 dfs1(1); 133 134 memset(vis,0,sizeof(vis)); 135 memset(dis,0,sizeof(dis)); 136 path[start] = 0; 137 mdis = 0;end = 0; 138 139 dfs2(start); 140 141 memset(vis,0,sizeof(vis)); 142 memset(dis,0,sizeof(dis)); 143 for(int i = end;i;i = path[i]) dia[++cnt] = i,vis[i] = 1; 144 //求直径路径 145 //------------- 求最短路 146 Floyd(); 147 //-------------预处理 148 start = end = 0; 149 150 for(int i = 1;i <= n; ++ i){ 151 int cur = 2e9; 152 for(int j = 1;j <= cnt; ++ j){ 153 if(cur > g[i][dia[j]]){ 154 cur = g[i][dia[j]]; 155 dis[i] = g[i][dia[j]];//这是i到直径的最短距离 156 tmp[i] = j;//这是相应编号 157 } 158 } 159 } 160 //------------左右边界 161 int l = 0,r = (mdis >> 1) + 1 + mw; 162 for(int i = 1;i <= n; ++ i) { 163 l = max(l,dis[i]); 164 } 165 //------------二分答案 166 int ans; 167 while(l <= r){ 168 int mid = (l + r) >> 1; 169 if(check(mid)) ans = mid,r = mid - 1; 170 else l = mid + 1; 171 } 172 put(ans); 173 } 174 175 int main(){ 176 // file(); 177 readdata(); 178 work(); 179 return 0; 180 }
非做顽石不可,哪管他敬仰暗唾



