数据结构与算法（1）----->排序

 

 

　　这一版块，把必备的数据结构和算法做一个总结！包括排序、队列、链表、二叉树、排组合，动态规划......。

　　总结的过程包括理论部分，练题目可以自己去leetcode/牛客网刷起来～

　　第一篇文章讲排序～

 

1.  经典的排序算法

　　分为时间复杂度为 O（n的平方）的： 冒泡排序、选择排序、插入排序;

　　时间复杂度为 O（ n 乘 log N）的： 归并排序、快速排序、堆排序、希尔排序

　　时间复杂度为 O（n）的排序算法：计数排序算法、基数排序算法;

 

1.1  冒泡排序

　　冒泡排序的时间复杂度为 O（n的平方）。

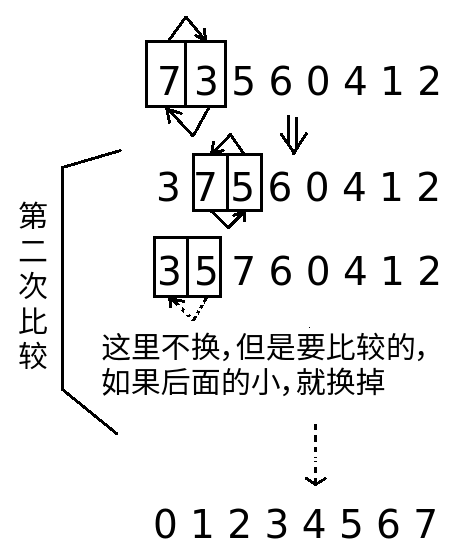
　　例如一个数组：    7 3 5 6 0 4 1 2

　　冒泡排序思路：（对比下图来看）

1. 第一次交换区间是0～N-1，第一和第二个数字进行比较，大的数字放在后面;接着第二第三个数字进行比较，同样，大的放在后面。如此，依次进行交换，直到换到最后一个数N-1。这样，最大的数字就到了N-1位置;
2. 第二次交换的区间变为0～N-2（最后一个数字不需要再移动了），比较方法类似步骤一;最后，第二大的数字到达了N-2的位置;
3. 依次交换，直到最后一次交换区间变为0，整个数组此时已经变得有序，结束。

　　图画得有点丑，将就着看吧～

 

1.2  选择排序

　　选择排序的时间复杂度为 O（n的平方）。

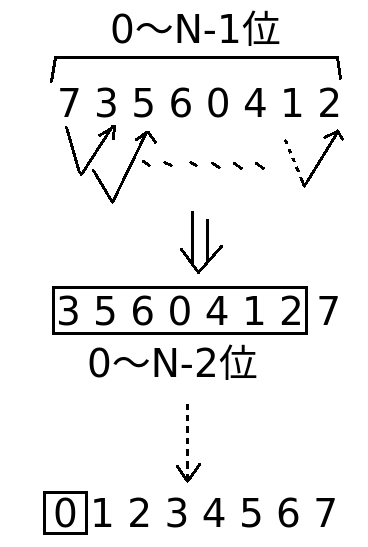
　　例如一个数组：    7 3 5 6 0 4 1 2

　　选择排序思路：

1. 第一次在区间0～N-1中，选出数组的最小值放到位置0上;
2. 第二次在在区间1～N-1中，选出最小值放到位置1上;
3. 依次选择，直到最后选择到最后的数值，放到N-1位置上;结束。

 　　这个图画得好看点儿了吧～

 

1.3  插入排序

　　插入排序的时间复杂度为 O（n的平方）。

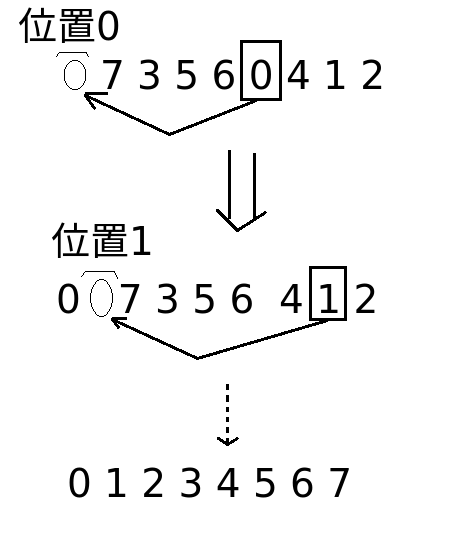
　　例如一个数组：    7 3 5 6 0 4 1 2

　　插入排序思路：

1. 第一次，对第0和第1位置上的数字进行比较小放左边（前），大的方右边（后）;
2. 第二次，对第1位置和第2位置进行比较，选出较小值放到位置1上，较大值也就到了第2位置;这个时候需要对第1位置和第2位置再次进行比较，最小的放到最前;
3. 依次比较下去，直到最后比较到最后的第N-1位置的数值和第N-2位置大的数值比较，较小的依次与前面的各个位置比较置换，比较到第0和第1位置之后结束。

 　　画图好麻烦啊！！

 

1.4  归并排序

　　归并排序的时间复杂度为  O（ n 乘 log N）。

　　例如一个数组：    7 3 5 6 8 4 1 2

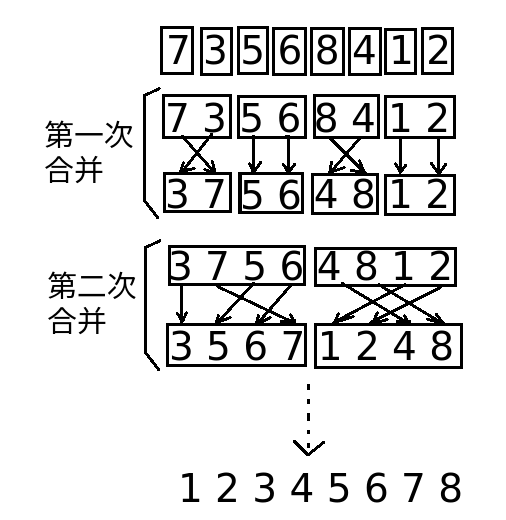
　　归并排序思路：

1. 第一次，把划分成为N个小区间;相邻两两区间进行合并，得到N/2个有序区间
2. 第二次，把相邻的区间再次合并，得到N/4个有序区间;
3. 依次类推，直到把最后两个有序区间合并成一个区间，结束;

 　　如图：

 

 

1.5  快速排序（划重点！！！很重要）

　　快速排序的时间复杂度为 O（ n 乘 log N）。

　　例如一个数组：    7 3 5 6 0 4 1 2

　　快速排序思路：

1. 随机选择数组中的一个元素，把小于等于该数的元素统一放在数组的左边，大于该数的元素放在数组的右边;
2. 分别对左右两个部分，再次采用快排思路，随机在期间找一个元素，同样，大于的右侧，小于等于的放在左侧;
3. 依次递归下去，完成排序。

 　　画图好麻烦啊！！

 

1.6  堆排序

　　堆排序的时间复杂度为 O（ n 乘 log N）。

　　例如一个数组：    7 3 5 6 0 4 1 2

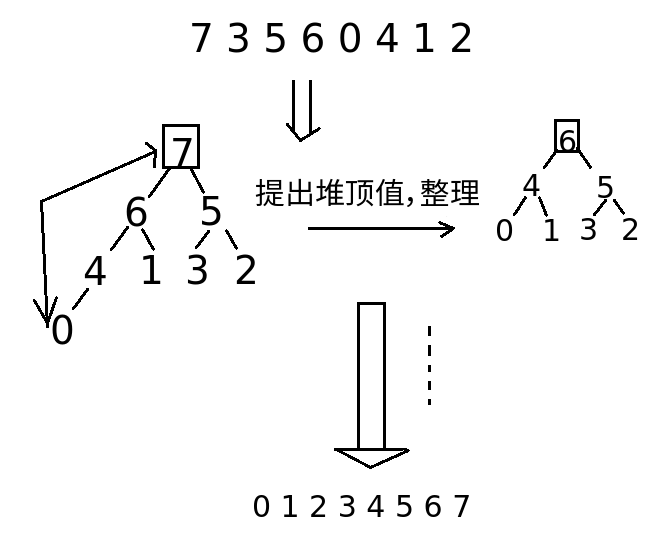
　　堆排序思路：

1. 将堆写成由大到小的堆分支;堆顶为最大值
2. 将堆顶元素提出，堆顶元素放到右侧，脱离堆;
3. 将新的堆（N-1个元素）进行调整，重复步骤1、2，直到完成最后一个元素，结束。

 　　画图好麻烦啊！！

 

1.7  希尔排序

　　希尔排序的时间复杂度为 O（ n 乘 log N）。希尔排序是插入排序的一种改良做法。

　　插入排序前面已经介绍过了，可以知道，插入排序是1位一位往前比较的（步长为1）。而希尔排序初始步长为 >1,遍历结束之后步长减少1，直到最后步长为1时遍历完成，这样结束。

　　例如一个数组：    7 3 5 6 0 4 1 2

　　希尔排序思路：

1. 假设初始步长为3（自己设置的），从第四位元素和第一位元素进行比较，大小为逆序则交换两者位置，大小为顺序则保留原位置;
2. 接着比较第5位和第2位（5往前跑步长3啊），同理，大小为逆序则交换两者位置，大小为顺序则保留原位置;
3. 依次类推，完成这一轮次的比较;
4. 接着降低步长变为2，同样的方法
5. 最后步长为1，遍历完成后结束排序。

 　　下面这个图做的是步长为3的，降低步长方法一致，这里不画了～

 

 

1.8  计数排序（源于桶排序思想）

　　时间复杂度为O（N）。举个例子说明他的思想。

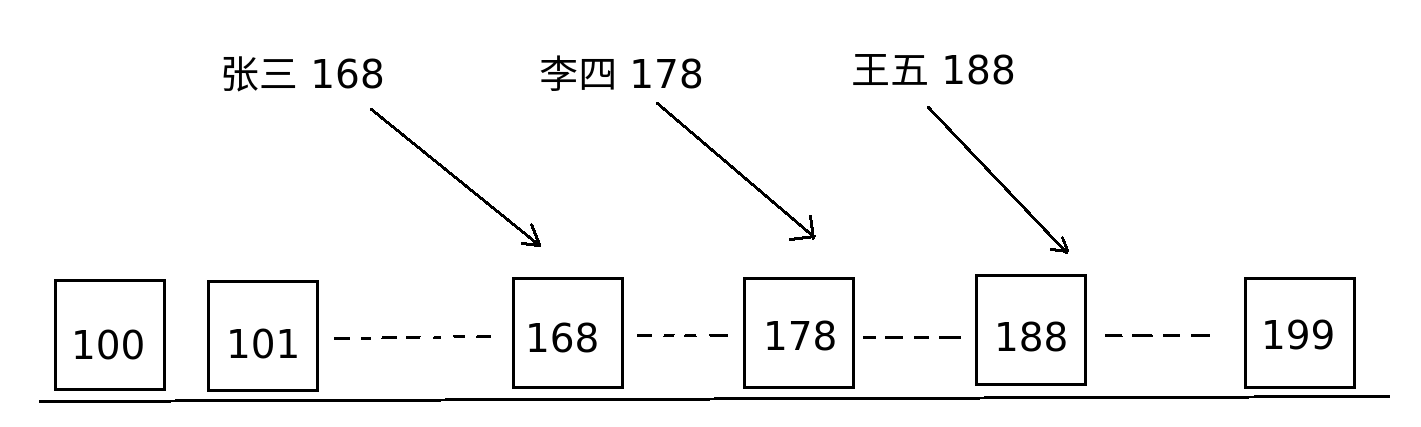
　　例如：对   张三（168）  李四（178）  王五（188）  的身高排序;

　　其思路是，建立N个桶，比如100，101，102,...,199(共100个桶)，接着将张三，李四，王五放入自己对应的桶中。最后，依次将100～199桶中的数倒出来，也就得到了他们的身高顺序了。

　　看图：

 

1.9  基数排序 （源于桶排序思想）

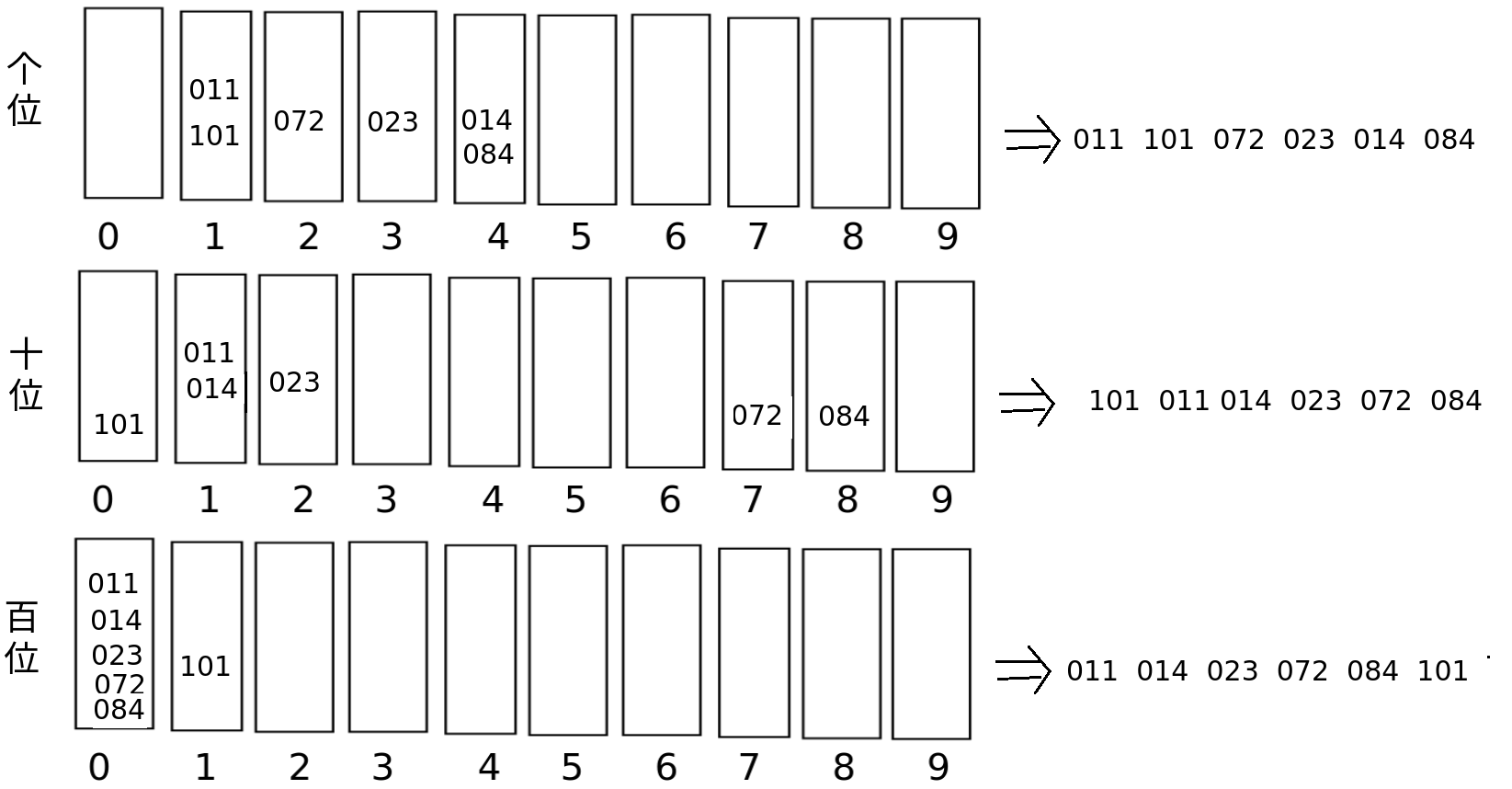
　　数组元素本身，先按照个位进行排序，放入0～9号桶中;再按照十位排序，放到桶中，依次上升百位...

　　例如： 对  011   014   023   072   084   101  进行排序

 

 

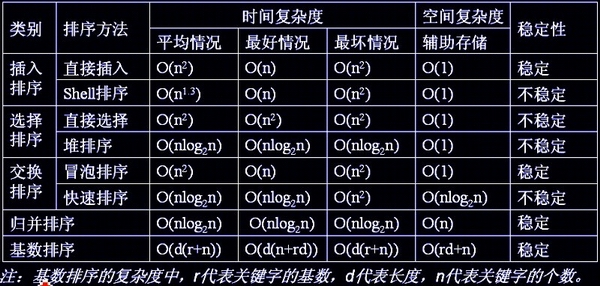
2.  经典排序算法空间复杂度、稳定性

　　空间复杂度：

空间复杂度	算法
O（1）	插入排序、选择排序、冒泡排序、堆排序、希尔排序
O（log N）	快速排序
O（N）	归并排序
O（M）	计数排序、基数排序

 　　稳定性：（是否破坏相邻性，破坏则不稳定）

稳定的排序算法	插入排序、冒泡排序、归并排序、计数排序、基数排序、桶排序
不稳定的排序算法	希尔排序、选择排序、快速排序、堆排序

 

 

　　附：