数据结构-第8章学习小结

第八章  排序

一、整理大概的学习脉络

 

 

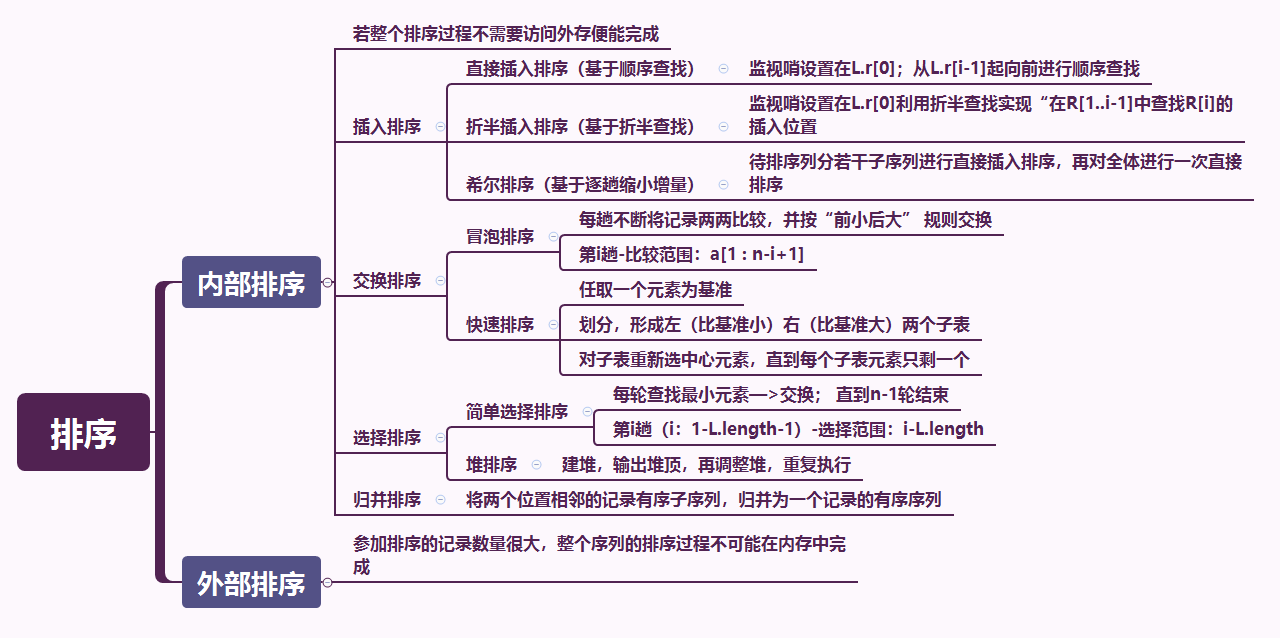
二、重点

（一）快排

1. 算法

//主函数调用语句： QKSort ( L, 1, L.length ); 

void QKSort(SqList &L, int low, int high)
{
    int pos;
    if(low < high)//递归退出条件为low == high
    {
        pos = Partition(L, low, high);//划分
        QKSort(L, low, pos - 1);//排左边
        QKSort(L, pos + 1, high);//排右边
    }
}

int Partition ( SqList &L，int low,  int  high) 
{
    L.r[0] = L.r[low]; //选择 L.r[low]为基准
    pivotkey = L.r[low].key;//以基准的key值来划分成左右子表
    while (low < high) 
   { 
         while(low<high && L.r[high].key>=pivotkey)  
                  --high;//从high开始向左查找小于 L.r[high].key的数据对应下标
         L.r[low] = L.r[high];//并覆盖到下标low的位置

         while(low<high && L.r[low].key<=pivotkey )  
                   ++low;//从low开始向右查找大于 L.r[low].key的数据对应下标
         L.r[high] = L.r[low];//并覆盖到下标high的位置
     }
     L.r[low]=L.r[0]; 
     return low;//基准的确定位置下标
}

2. 算法分析

• 时间效率：O(nlog2n) —— 每趟确定的元素呈指数增加

【最坏情况为排序数据为有序数据——>O(n^2)——>避免最坏情况——>{①随机算法（洗牌、划分前随机找一个数交换到最前面）②基准找L.r[low]、L.r[high]、L.r[low+high]三者的中间数}】

• 空间效率：O（log2n）—— 递归要用到栈空间

• 稳 定 性： 不稳定（涉及远处交换） —— 可选任一元素为支点。

3. 变形应用——找第k小

（二）堆排

1. 堆：n个元素的线性序列{k1,k2,…,kn}，且满足

 

 【注意：完全二叉树只作为堆的描述工具】

2.建堆（要获得非降序排列——>利用大根堆）

（1）按层次将堆中元素组织为完全二叉树

（2）从下往上——>推最大值到根（建立大根堆）

（3）从上往下调整

3. 调整堆——从下往上，从树的最后一个非终端结点开始调整【非终端结点：对n个结点的完全二叉树，其对应n/2的结点】

4.时间效率：O(nlog2n) ;  空间效率：O(1);  稳 定 性：不稳定

5. 堆排序变形应用——top k问题（一次建堆，k次调整）

 

三、排序算法分析比较

 

 

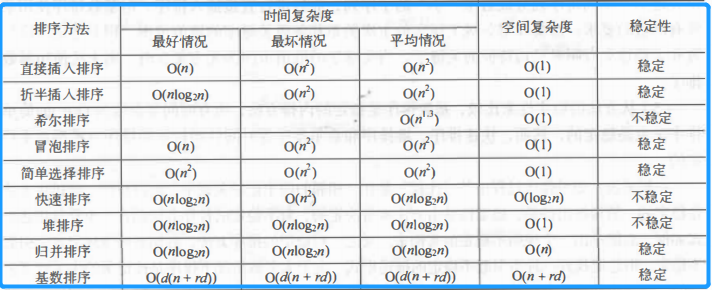
四、心得体会

作业题“统计工龄”直接用来数组下标（类似投票那种）来弄，还没想到要怎么用排序来弄，感觉好像没有直接用数组下标来简单？然后客观题的话更多考察对不同排序方法的理解以及排序算法复杂度的对比分析（可能还没有掌握的很好，做起来有点晕），所以还是要好好对不同排序方法是适用场景，特点，算法与初始序列的关系进行对比分析好一些（由于时间关系，后续再进行补充（捂脸.jpg））