数据结构-第6章学习小结

第六章——图

一、学习内容架构

 

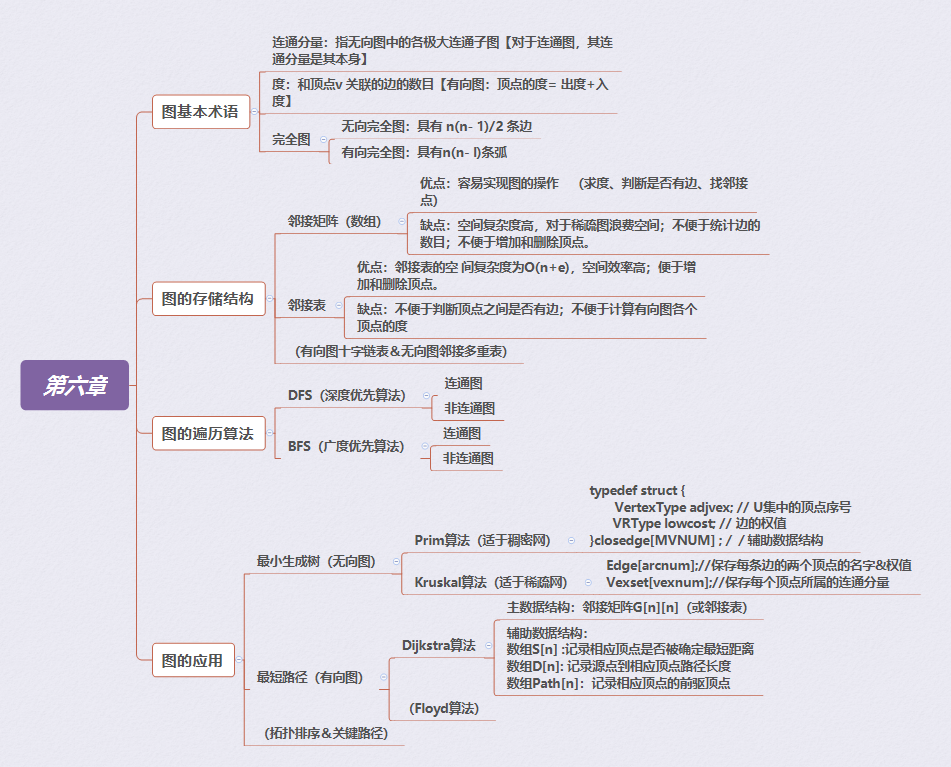
二、基于邻接矩阵与基于邻接表的图结构定义对比

 

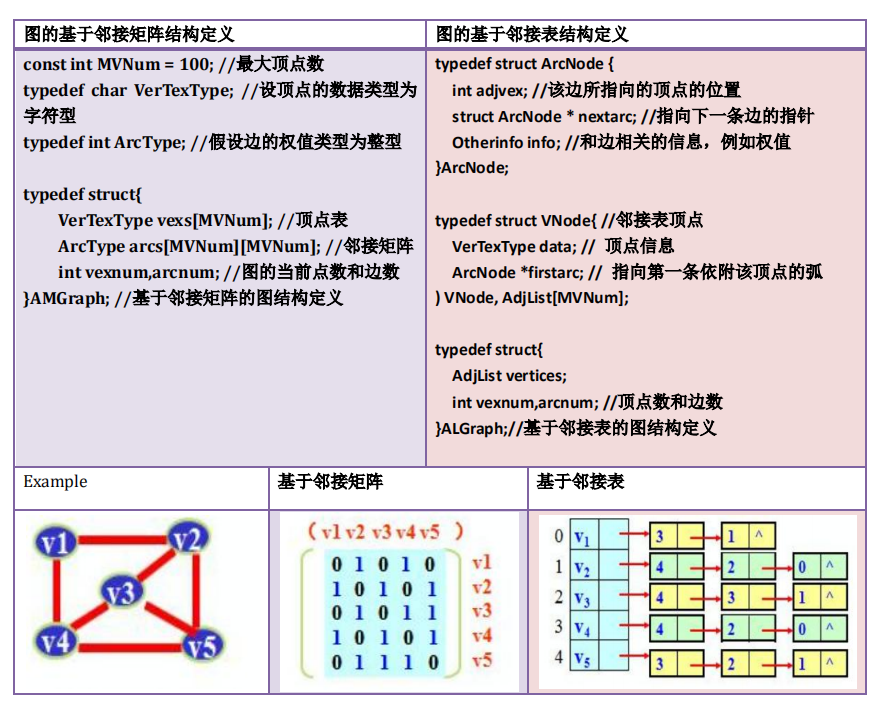
三、算法

1、DFS算法

void DFS(Graph G, int v)
{//从顶点v出发，深度优先搜索遍历连通图 G
    visited[v] = true;
    for(w = firstAdjvex(G, v); w>=0; w = NextAdjVex(G,v,w))
    {
        if(!visited[w]) DFS(G,w);// 对v的尚未访问的邻接顶点w递归调用DFS
    }
 } //连通图的深度优先遍历算法（未考虑具体图的存储结构） 

void DFST(Graph G)
{
    for (v=0; v<G.vexnum; v++)
        visited[v] = false;//初始化访问标志数组 

    for (v=0;v<G.vexnum;v++) 
        if(!visited[v]) DFS(G,v);//对还未访问的顶点调用DFS 

} //非连通图的深度优先遍历算法（需要调用连通图的DFS算法）

//基于邻接矩阵的图的DFS算法
void DFS_AM(AMGraph G, int v)
{
    cout << v ;//访问第v个顶点 
    visited[v] = true;//访问过则设为true 
    for(w=0; w<G.vexnum; w++)//依次检查邻接矩阵所在的行
       if((G.arcs[v][w]!=0)&&(!visited[w])) //如果w是v的邻接点且w未访问
           DFS_AM(G,w); //递归调用DFS_AM
}

//基于邻接表的图的DFS算法
void DFS_AL(ALGraph G, int v)
{
    cout << v; //访问第v个顶点
    visited[v] = true;//访问过则设为true 
    p = G.vertices[v].firstarc;//p指向v的边链表的第一个边结点
    while(p!=NULL) //边结点不为空
    {
        w = p->adjvex; //w是v的邻接点
        if(!visited[w]) //w未访问
           DFS_AL(G, w);//递归调用DFS_AL
        p = p->nextarc; //p指向下一个边结点    
    }
         
}

2、BFS算法

void BFS(Graph G, int v)
{
    cout<<v; //访问第v个顶点
    visited[v] = true;//访问过则设为true 
    InitQueue(Q); //辅助队列Q初始化，置空
    EnQueue(Q, v); //v进队
    while(!QueueEmpty(Q))
    { //队列非空 
        DeQueue(Q, u); //队头元素出队并置为u
        for((w = FirstAdjVex(G, u); w>=0; w = NextAdjVex(G, u, w)))
        {
            if(!visited[w])
            {//w为u尚未访问的邻接顶点
                cout<<w;
                visited[w] = true;
                EnQueue(Q, w); //w进队
            }
            
        } 
}//连通图的BFS算法（未考虑具体图的存储结构）

void BFST(Graph G)
{//基本与DFST一样，只是将DFS(G,w)改为BFS(G,v)
    for (v=0; v<G.vexnum; v++)
        visited[v] = false;//初始化访问标志数组 

    for (v=0;v<G.vexnum;v++) 
        if(!visited[v]) BFS(G,v);//对还未访问的顶点调用BFS
      
} //非连通图的深度优先遍历算法（需要调用连通图的BFS算法）

//基于邻接矩阵的图的BFS算法
void BFS(Graph G, int v)
{
    cout<<v; //访问第v个顶点
    visited[v] = true;//访问过则设为true 
    InitQueue(Q); //辅助队列Q初始化，置空
    EnQueue(Q, v); //v进队
    while(!QueueEmpty(Q))
    { //队列非空 
        DeQueue(Q, u); //队头元素出队并置为u
        for((w = 0; w<G.vexnum; w++)
        {
            if(!visited[w] && G.arcs[u][w]==1)
            {//w为u尚未访问的邻接顶点
                cout<<w;
                visited[w] = true;
                EnQueue(Q, w); //w进队
            }    
        } 
    }
}

//基于邻接表的图的BFS算法
void BFS(Graph G, int v)
{
    cout<<v; //访问第v个顶点
    visited[v] = true;//访问过则设为true 
    InitQueue(Q); //辅助队列Q初始化，置空
    EnQueue(Q, v); //v进队
    while(!QueueEmpty(Q))
    { //队列非空 
        DeQueue(Q, u); //队头元素出队并置为u
        p = G.vertices[u].firstarc;//p指向u的边链表的第一个边结点
        while(p!=NULL) //边结点不为空
        {
            w = p->adjvex; 
            if(!visited[w]) 
            {//w未访问
                cout << w;
                visited[w] = true;
                EnQueue(Q, w); //w进队 
            }
            p = p->nextarc; //p指向下一个边结点    
        }
    }
}

3、prim算法（最小生成树——加点法）

/*
typedef struct { 
   VertexType adjvex; // U集中的顶点序号 
   VRType lowcost; // 边的权值 
}closedge[MVNUM];
*/ 
void MiniSpanTree_P(AMGraph G, VertexType u)
{//从顶点u出发构造网G的最小生成树
    k = LocateVex ( G, u );//定位顶点u的下标 
    for ( j=0; j<G.vexnum; ++j ) // 辅助数组初始化
       if (j!=k) closedge[j] = { u, G.arcs[k][j].adj };//{adjvex, lowcost} 
    
    closedge[k].lowcost = 0; // 初始，U＝{u}
    int weights = 0;//计算最小生成树权值之和 
    for (i=1; i<G.vexnum; ++i)
    {
        // 求出加入生成树的下一个顶点(k)
        k = Min(closedge[] | closedge[].lowcost>0);//查找closedge[]中lowcost>0且最小的顶点
        cout << closedge[k].adjvex << G.vexs[k];
        weights += closedge[k].lowcost;//每次归并到U集lowcost未置0前先把权值加到weights 
        closedge[k].lowcost = 0; // 第k顶点并入U集
    }
    
    for (j=0; j<G.vexnum; ++j) //修改其它顶点的最小边 
        if (G.arcs[k][j] < closedge[j].lowcost) 
            closedge[j] = { G.vexs[k], G.arcs[k][j] }; 

} 

4、Kruskal算法（最小生成树——加边法）

/*typedef struct{
    VerTexType Head; //边的始点 
    VerTexType Tail; //边的尾点 
    ArcType lowcost; //边权值 
} Edge [ arcnum] ;  

int Vexset[MVNum];//标识各个顶点所属的连通分量。 
*/

void  Kruskal(AMGraph G) 
{//无向网G以邻接矩阵形式存储，构造G的最小生成树T, 输出T的各条边
    Sort (Edge); //将数组 Edge中的元素按权值从小到大排序
    for(i=O;i<G.vexnum;++i) 
        Vexset[i]=i; //初始化辅助数组，表示各顶点自成一个连通分址
    for(i=O;i<G.arcnum;++i)
    {//依次查看数组 Edge 中的边
        v1=LocateVex(G, Edge[i].Head);//vl为边的始点Head的下标
        v2=LocateVex(G, Edge[i].Tail);//v2为边的终点Tail过的下标
        vs1=Vexset[vl]; //获取边Edge[i]的始点所在的连通分量 vs1 
        vs2=Vexset[v2]; //获取边Edge[i]的始点所在的连通分量 vs2 
        if(vsl!=vs2) 
        {//的两个顶点分属不同的连通分量 
            cout<< Edge[i].Head << Edge[i].Tail;//输出此边
            for(j=O;j<G.vexnurn;++j) //合并VS1和VS2两个分量，即两个集合统一编号
                if(Vexset[j] ==vs2) 
                    Vexset[j] =vs1; //集合编号为 vs2 的都改为 vsl
        }         
    }
}

5、Dijkstra算法（求有向图最短路径）

/*
辅助数据结构：
数组S[n] :记录相应顶点是否被确定最短距离
数组D[n]: 记录源点到相应顶点路径长度
数组Path[n]：记录相应顶点的前驱顶点
*/

void Dijkstra (AMGraph G, int v0) 
{//用Dijkstra算法求有向网G的v0顶点到其余顶点的最短路径
        n=G.vexnum; //n为G中顶点的个数
        for (v= 0;v<n; ++v)
        {//初始化
            S[v]=false; //S初始为空集
            D[v]=G.arcs[v0][v];//初始化为弧上的权值
            if(D[v]<INT_MAX) Path[v]=v0; //有弧，前驱置为v0 
            else Path[v] = -1; //无弧,前驱置为-1
        } 
        S[v0] = 1;//将vO加入S
        D[v0] = INT_MAX;//源点到源点的距离为无穷大 
        
        for(i=1;i<n;i++)
        {//选择 
            min=INT_MAX;
            for(w= O;w<n;w++)
            {//选择一条当前的最短路径，终点为v
                if (S[w]==0 && D[w]<min)
                {
                    v = w;
                    min = D[w];
                }
            }
            S[v] = 1 ;//将v加入S    
        }
        
        for(j=1;j<n;j++)
        {//刷新 
            if (S[w]==0 && (D[v]+G.arcs[v][w] <D [w]))
            {
                D [w] =D [v] +G. arcs [v] [w]; //更新 D[w]
                Path[w]=v; //更改w的前驱为v
            }
        }

}

 

四、本章学习心得

1、一开始好多术语看的比较乱，后来小测上课讲解后更好的理解了。还有对于图 的结构定义的取名自己真的一开始好乱（即使老师有说要看好哪个名字对应哪个数据结构）但是还是有点乱，要看多几遍才没那么乱ฅʕ•̫͡•ʔฅ

2、图的遍历经过上课的演示跟小测题目以及PTA作业后，对于DFS以及BFS算法的理解掌握还算较好。

3、总体感觉自己这章图的应用学的有点乱，对于最短路径跟最小生成树的算法学的时候不乱，都学完后就乱了，然后经过算法重重新的整理及理顺，现在觉得清晰很多。

4、有向图十字链表&无向图邻接多重表，最短路径Floyd算法，拓扑排序&关键路径老师没有安排教学，自己看了有点头疼😂

5、实践题注意也要用一个辅助数组来记录是否以及跳过

 

五、易错点

1、使用邻接矩阵a存储无向网络，若i号顶点与j号顶点之间不存在边，则a[i][j]值为多少——若权值是一个正整数，可以设为0或负数。若权值是整数，则设为一个大于所有边权值的数（INT_MAX)

2、最小生成树不一定唯一（看图直接找，有可能不唯一），但是用算法来查找的最小生成树一般是唯一的（算法是确定性算法，即对于同样的输入得到的一定是相同的输出）【但是算法里如果使用了随机数进行运算，那结果就不保证都一样了】

3、使用遍历算法时，visited数组设为全局变量比较方便