字符串匹配--Java实现Sunday算法
简介
Sunday算法是Daniel M.Sunday于1990年提出的字符串模式匹配
参考:https://blog.csdn.net/q547550831/article/details/51860017
核心思想
在匹配过程中,模式串并不被要求一定要按从左向右进行比较还是从右向左进行比较,它在发现不匹配时,算法能跳过尽可能多的字符以进行下一步的匹配,从而提高了匹配效率
简单介绍相关的相关定义:
- 下文实现均为在主串中找模式串
- 关注字符:Sunday算法在匹配失败时,关注的字符为参与匹配的最末字符的下一位
例子说明
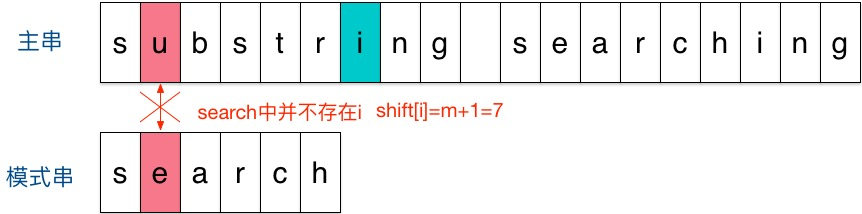
假定现在要在主串”substring searching”中查找模式串”search”,如下图
-
此时发现在第2个字符处发现不匹配,不匹配时关注主串中参加匹配的最末位字符的下一位字符,即标为蓝绿色的字符I
注:(由于字符串需要完整匹配上,则下一位字符一定需要出现在模式串中)
因为模式串search中并不存在i,所以【U->I】之间的字符都可以跳过,向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7,从 i 之后的那个字符(即字符n)开始下一步的匹配,如下图

-
移动后第一个字符就不匹配,再看主串中参加匹配的最末位字符的下一位字符,是’r’,它出现在模式串中的倒数第3位,这是需要将主串中的字符‘r’与模式串中的’r‘对齐,于是把模式串向右移动3位,(m - 3 = 6 - 3 = r 到模式串末尾的距离 + 1 = 2 + 1 =3),使两个’r’对齐,如下图
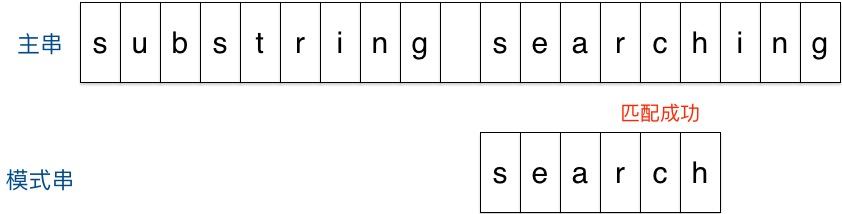
时间复杂度在O(m/n) –> O(m*n)的级别
总结:
Sunday算法是从前往后匹配,在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。
- 如果该字符没有在模式串中出现则直接跳过,即移动位数 = 模式串长度 + 1;
- 否则,其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。
缺点:Sunday算法的移动是取决于模式串的,当主串与模式串重复过多的时候,移动的效率会比较差
Java代码示例
int sundaySearch(String ts, String pattern) {
int[] next = getNext(pattern);
char[] t = ts.toCharArray();
char[] p = pattern.toCharArray();
int destLen = ts.length();
int patternLen = pattern.length();
for (int i = 0; i <= destLen - patternLen;) {
//主串位置
int j = i;
//模式串位置
int k = 0;
//循环判断字符是否匹配
for (; k < patternLen && j < destLen && t[j] == p[k]; j++, k++){
}
if (k == patternLen)
return i;
else {
//匹配失败时 计算移动步长
//由于一开始next数组默认置为-1,当此字符在next中不存在时,即移动步数为patternLen + 1
if (i + patternLen < destLen){
i += (patternLen - next[t[i + patternLen]]);
} else{
return -1;
}
}
}
return -1;
}
/**
* 判断模式串中是否包含某一字符
* 利用字符作为next数组的下标,保证获取字符复杂度为O(1)
* 默认模式串中不包含中文,假如需要包含中文可将数组大小修改为65536或采用其他方式实现
* @param pattern
* @return
*/
int[] getNext(String pattern) {
char[] p = pattern.toCharArray();
//字符ASCII一共256个 此处定义英文字符
int[] next =new int[256];
int len = pattern.length();
//默认置为-1
for (int i = 0; i < 256; i++)
next[i] = -1;
// 将模式串中出现的字符置为位置
for (int i = 0; i < len; i++)
next[p[i]] = i;
return next;
}


