操作树学习笔记

前言

这个数据结构(或许不是数据结构而仅仅是一种暴力?)比较冷门，网上也没找到什么博客。我尽量讲得详细。

昨天做一道CF的题目的时候就遇到了"操作树"。

昨天看到操作树，因为看的博客讲的没那么详细，而且比较抽象，一直没有想明白，然后晚上睡觉的时候YY出来应该怎么弄了。

这东西蛮简单的，比较低级，但是有些时候却挺有用的。

一般可以用操作树的题目：

• 允许离线（这是最重要的）

• 需要查询历史版本

• 当前操作受到之前操作的影响。

• 需要维护的状态不是那么复杂

操作树该怎么建

以这道题目为例：

CF707D Persistent Bookcase

题意搬运：

维护一个二维零一矩阵（\(n,m<=1000\)），支持四种操作（不超过\(10^5\)次）:

• 将\((i,j)\)置一
• 将\((i,j)\)置零
• 将第i行\(01\)反转
• 回到第\(K\)次操作后的状态\((K\)可以为\(0)\)
• 每次操作后输出全局一共有多少个\(1\)

思路

emmmm,感觉很像某种可持久化数据结构，但是蒟蒻实在想不出来该用啥。

But，操作树可以很轻松的解决这个问题。

这个问题没有强制在线

对于一个操作\(i\)我们发现倘若它不是第四种操作，它可以从自己的上一个操作转移来。

因为你是沿用的上一次操作的状态来对当前状态做出修改。

我们实际上要运用上一次修改后的状态进行修改。

那么对于非操作4的操作，我们想到建一条边\(i-1,i\)，表示操作\(i-1\)的状态可以转移到操作\(i\)，也就是操作\(i\)仍然需要它的状态。

实际上对于操作\(4\)也是一样的，我们连一条边\(K,i\)，不需要连\(i-1,i\)，这样即可。因为操作4只需要知道第\(K\)次操作后的状态，于是我们用操作\(K\)的状态来转移。

我们来模拟一下建树的过程：

先是状态0，全部都是0，没有修改之前。

然后有了操作1,它沿用的操作0的状态（即初始状态）

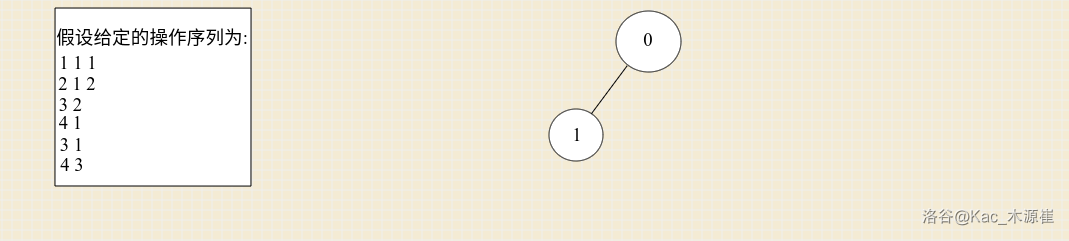
接着有了操作二，它需要沿用操作\(1\)的状态

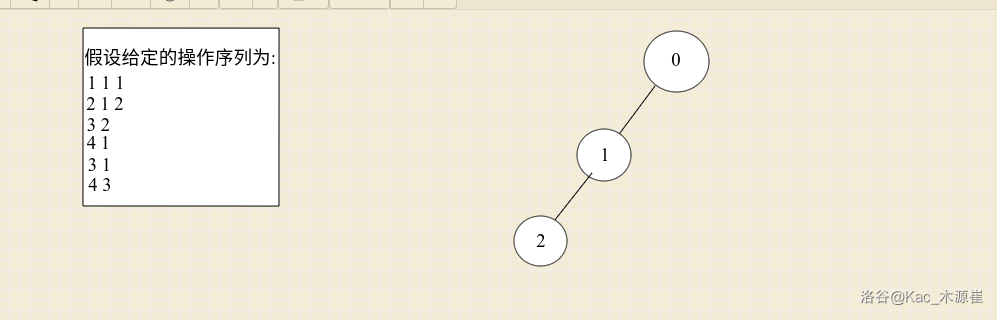
再是操作三,它沿用操作２的状态:

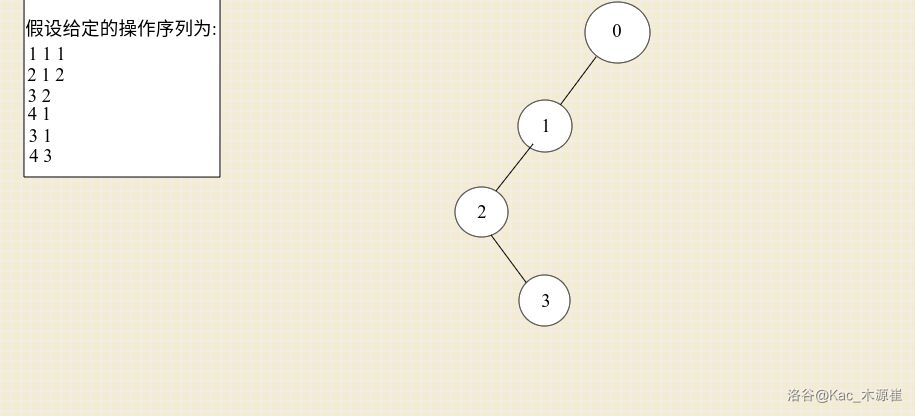
后来是操作４，注意，它属于操作类型４，它需要访问第１次修改后的状态，于是将操作４连到操作１下面:

然后又来了一个操作５，这个操作应该沿用操作４的状态，于是连到操作４的下面。

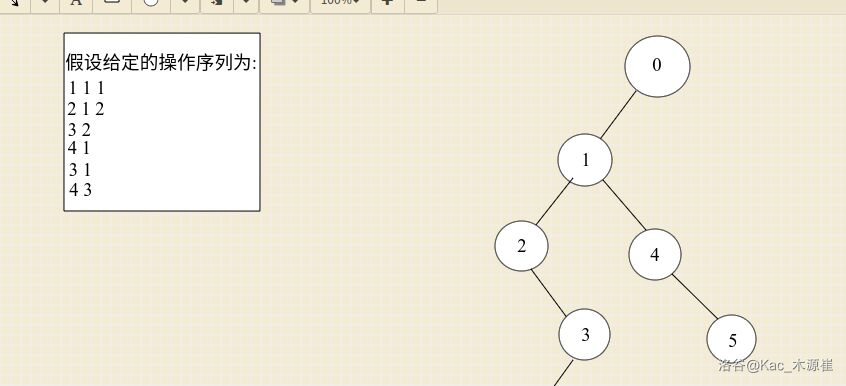
最后是操作６，注意，它属于操作类型４，它需要沿用操作３的状态，于是将操作６连到操作３的下面

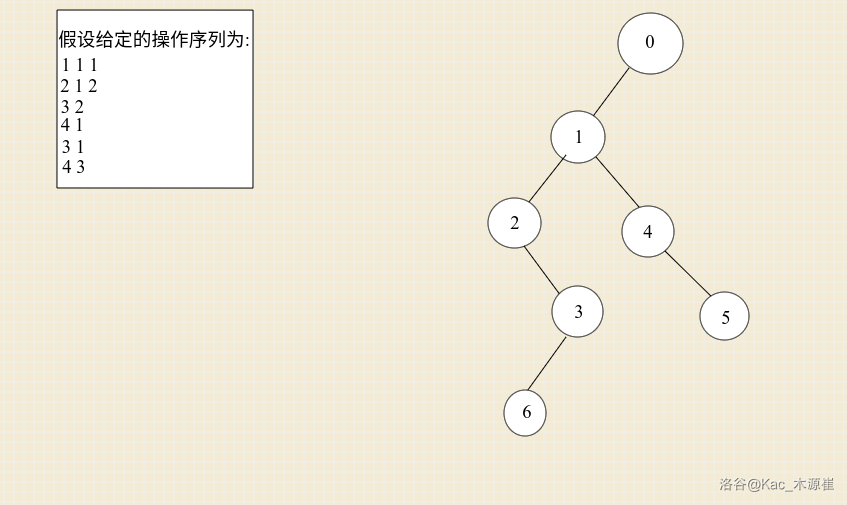
然后就建树完成了！(这是最核心的一部分)

怎么获得答案？对这棵树进行\(DFS\)，对于操作１，２，３就暴力修改，用\(bitset\)即可，然后对于操作４我们不需要修改，直接沿用前面的状态即可。

遍历完后记得回溯，具体看代码。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005,MAXM = 1005;
bitset <MAXM> All,P[MAXM];//All全部为１，便于对一整行取反

int n , m , Q;
int start[MAXN],cnt = 0;
int Ans[MAXN];

struct Node {
	int op,x,y,id;
} T[MAXN];

struct Edge {
	int next,to;
} edge[MAXN];

void add(int from,int to)
{
	cnt ++;
	edge[cnt].to = to;
	edge[cnt].next = start[from];
	start[from] = cnt;
	return ;
}

void DFS(int x,int from,int Now)//x表示当前节点，from表示当前节点的父亲节点，Now表示的是当前状态的答案
{
	bool q = 0;
	if(T[x].op == 1)
	{
		q = P[T[x].x][T[x].y];
		if(P[T[x].x][T[x].y] == 0)Now ++;//更新答案
		P[T[x].x][T[x].y] = 1;//直接修改
	}
	if(T[x].op == 2)
	{
		q = P[T[x].x][T[x].y];
		if(P[T[x].x][T[x].y] == 1)Now --;//更新答案
		P[T[x].x][T[x].y] = 0;
	}
	if(T[x].op == 3)
	{
		int A = P[T[x].x].count();//原来有多少个１
		P[T[x].x] ^= All;//暴力修改
		Now += P[T[x].x].count() - A;//统计现在的１的个数减去原来１的个数即是答案
	}
      //对于操作４不需要做出修改，直接沿用上次操作的答案即可
	Ans[T[x].id] = Now;//将答案塞进答案序列
	for(int i = start[x] ; i ; i = edge[i].next)
	{
		int to = edge[i].to;
		if(to != from)DFS(to,x,Now);//遍历
	}
	if(T[x].op <= 2)P[T[x].x][T[x].y] = q;//状态回溯
	if(T[x].op == 3)P[T[x].x] ^= All;//状态回溯
	return ;
}

inline int read()
{
	int x = 0, flag = 1;
	char ch = getchar();
	for( ; ch > '9' || ch < '0' ; ch = getchar())if(ch == '-')flag = -1;
	for( ; ch >= '0' && ch <= '9' ; ch = getchar())x = (x << 3) + (x << 1) + ch - '0';
	return x * flag;
}

int main()
{
	n = read() , m = read() ,Q = read();
	for(int i = 1 ; i <= m ; i ++)All[i] = 1;
	for(int i = 1 ; i <= n ; i ++)P[i].reset();//全部置0
	T[0].x = T[0].y = 0;
	for(int i = 1 ; i <= Q ; i ++)
	{
		T[i].op = read();T[i].id = i;//离线操作的常用套路，记录它的第几个询问
		if(T[i].op <= 2)T[i].x = read(),T[i].y = read();
		else T[i].x = read();
		if(T[i].op <= 3)add(i - 1 , i);//如果不属于操作４就连边i-1 to i
		else add(T[i].x,i);//如果属于操作４就连边K to i
	}
	DFS(0,0,0);//注意要从0开始遍历，因为K可以等于0！
	for(int i = 1 ; i <= Q ; i ++)cout << Ans[i] << endl;//输出答案即可
	return 0;
}

相信你们看了例子就学会建树了，就写到这里了。