分块--莫队学习粗略预习

分块&莫队学习总结

2020-08-12 16:55:32

thumb_up 0

---

大概就是暴力的进化版，采用：“大段维护，小段朴素”的思想

拿个板子说事：

已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 k。
求出某区间每一个数的和。

序列长度为1e5,操作数为1e5，裸的线段树板子

但是,今天我就是要用分块做！(然后T了三个点，可能是我脸黑)

分块的思路:

将序列划分成任意大小的块，注意是任意大小，视题目内容定，总是有些刻板印象硬是要固定块的大小为根号n，虽然这是最常见的，但是未必是最优的（就比如P4168蒲公英）。分好块后，可以确定每一个单点属于哪个块（预处理不要程序会慢一点，遇到毒瘤出题人....不可描述）。 接着，块长为Block的话，那么块数就是n/Block，如果你采用根号n，那么每次修改的时间复杂度都是根号n，其他的可以计算得出。然后就可以愉快的暴力了

这道模板，对于任意一个修改操作修改区间 [l,r]

1.l、r均属于块P，那么直接暴力修改，反正块长为根号n

2.l、r分别属于p、q，那么就维护一下块p+1到q-1，对l到p块的末尾，暴力修改， 对于r到q块的开端，暴力修改，中间的区间修改通过标记来处理

对于查询 ，基本同上

贴上我这因为脸黑 其实是我菜 打70分的分块代码:

#include <bits/stdc++.h>
using namespace std;
#define int long long
int n,m,num;
int a[100005],sum[100005],add[100005];
int l[20005],r[20005],pos[100005];
inline int read(){
    int sum=0;char ch=getchar();
    while(ch > '9' || ch <'0')ch=getchar();
    while(ch >= '0' && ch <= '9')
    sum=(sum<<3)+(sum<<1)+ch-'0',ch=getchar();
    return sum;
}
int change(int x,int y,int k);
int getans(int x,int y);
signed main(){
    cin>>n>>m;
    for (int i = 1 ; i <= n; i ++)cin>>a[i];
    int L,R,i=1;
    int block=(int)(sqrt(n));
    while(R != n){
        l[i]=block*(i-1)+1;
        r[i]=min(block*i,n);
        R=r[i];i++;
    }num=i;
    for (int i = 1 ; i <= num ; i++){
        add[i]=0;
        for (int j = l[i] ; j <=r[i] ; j ++)
        sum[i]+=a[j],pos[j]=i;
    }
    for (int i = 1 ; i <= m ; i ++){
        int op,x,y,k;
        op=read();
        if(op == 1)x=read(),y=read(),k=read(),change(x,y,k);
        if(op == 2)x=read(),y=read(),cout<<getans(x,y)<<endl;
    }
    return 0;
}
int change(int x,int y,int k){
    int p=pos[x],q=pos[y];
    if( p == q )for (int i = x ; i <= y ; i ++)a[i]+=k;
    else {
        for (int i = x ; i <= r[p] ; i ++)a[i]+=k;sum[p]+=(r[p]-x+1)*k;
        for (int i = y ; i >= l[q] ; i --)a[i]+=k;sum[q]+=(y-l[q]+1)*k;
        for (int i = p+1 ; i <= q-1 ; i ++)add[i]+=k;
    }
    return 0;
}
int getans(int x,int y){
    int p=pos[x],q=pos[y],ans=0;
    if( p == q ){for (int i = x ; i <= y ; i ++)ans+=a[i];return (ans+(y-x+1)*add[q]);}
    else {
        for (int i = x ; i <= r[p] ; i ++)ans+=a[i]+add[p];
        for (int i = y ; i >= l[q] ; i --)ans+=a[i]+add[q];
        for (int i = p+1 ; i <=q-1 ; i ++)ans+=sum[i]+(r[i]-l[i]+1)*add[i];
        return ans;
    }
}

8.19日，我修订了一下上面原有代码，然后A了。。。。

数列分块入门2：

题目链接：https://loj.ac/problem/6278

给出一个长为 n 的数列，以及 n 个操作，操作涉及区间加法，询问区间内小于某个值x 的元素个数。


 

题外话：

这玩意坑了我一个上午，woc我看了看题目是求小于，我一直求的是小于等于x的元素个数

思路：

首先分析一下题目中的性质，如果a<b,那么对于任意c>=0都有a+c<b+c，

所以我们的add操作如果覆盖了一整个块，那么其实在这一个块内的顺序是不会变的，所以我们只用处理旁边的没有覆盖一整块的区间

也就是零散的区间，就暴力处理，然后添加完对一整个块重新排序，查询操作就比较简单了，因为每一个块都是有序的，所以可以在整块内二分

如果是零散的区间，就直接暴力查询。

我先给每个块来个排序（块内排序），总时间复杂度O(nlogn)
然后要记录下块里面每个块在原来对应的位置，这个时间复杂度几乎忽略不计（我可以开结构体啊）
1.对于每一个查询，

1.1零散的不足一块的我就直接暴力查询有多少个比当前查询值要小的，
1.2对于整块的我就二分（因为是排好序的）查询一下有多少个比当前查询值小的
2.对于每一个修改，

2.1零散不足一块的我就遍历这个块，如果这个点的原编号在修改区间内就修改最后重新对这一块排序就行了

2.2对于满足一块的就直接维护add数组

综上，总时间复杂度为：O(n*sqrt(n)*log(sqrt(n)))，n<=50000，很明显sqrt(n)不超过240，log(sqrt(n))不超过8，50000*240*8=9.6*10^7，这是最坏情况（也能跑过，如果你RP不那么低），

也就是n次操作全是查询而且每次查询都是1到n，但是实际跑出来的复杂度要远低于这个值的，所以，大胆暴力！！！

 

#include <bits/stdc++.h>
using namespace std;
#define int long long 
int n,m,t=0;
struct node{int data,id;}r[200005];
int L[100005],R[100005],block,pos[200005],add[200005];
int cmp(node A,node B){return A.data<B.data;}

int change(int x,int y,int k);
int query(int x,int y,int k);
signed main(){
    cin>>n;m=n;
    for (int i = 1 ; i <= n ; i ++)cin>>r[i].data,r[i].id=i;
    block=(int)(sqrt(n));
    while(R[t] != n){
        t++,L[t]=(t-1)*block+1;
        R[t]=min(t*block,n);//确定每一个块的边界
    }
    for (int i = 1 ; i <= t ; i ++){
        for (int j = L[i] ; j <= R[i] ; j ++)
        pos[j]=i,add[i]=0;
        sort(r+L[i],r+R[i]+1,cmp);//排序每一个块，这个加1一定要留，不然会Wa，我也不知道为什么
    }
    for (int i = 1 ; i <= m ; i ++){
        int op,x,y,k;
        cin>>op>>x>>y>>k;
        if(op == 0)change(x,y,k);
        else cout<<query(x,y,k*k)<<endl;
    }
    return 0;
}
int find(int x,int y,int num,int ttt){//二分查询，x是左端点，y是右端点，num是要查询的那个标准值，ttt是当前块的编号
    int s=x,mm=y;
    while(x < y){
        int mid=(x+y)>>1;
        if(r[mid].data+add[ttt] < num)x=mid+1;
        else y=mid-1;
    }
    while(r[x].data + add[ttt] >= num && x>=s)x--;//防止我二分爆炸
    if(x > mm)x=mm;
    return x-s+1;
}
int query(int x,int y,int k){
    int p=pos[x],q=pos[y];
    if(pos[x] == pos[y]){
        int total=0;
        for (int i = L[p] ; i <= R[p] ; i ++)
        if(x <=r[i].id&&r[i].id <= y && r[i].data+add[p] < k)
        total++;//暴力统计
        return total;
    }
    else {
        int total=0;
        for (int i = L[p] ; i <= R[p] ; i ++)
        if(x <=r[i].id && r[i].id  <= R[p] && r[i].data+add[p] < k)
        total++;
        for (int i = L[q] ; i <= R[q] ; i ++)
        if(L[q] <=r[i].id && r[i].id  <= y && r[i].data+add[q] < k)
        total++;//暴力统计
        for (int i = p +1 ; i <= q -1 ; i ++)
        total+=find(L[i],R[i],k,i);//直接二分查找当前块内的小于x的数
        return total;
    }
}
int change(int x,int y,int k){
    int p=pos[x],q=pos[y];
    if(pos[x] == pos[y]){
        for (int i = L[p]; i <= R[p] ; i ++)
        if(x <= r[i].id && r[i].id  <= y)r[i].data+=k;
        sort(r+L[p],r+R[p]+1,cmp);//如果是小块就直接修改
　　　　//因为不是整段都被覆盖，所以有一部分是被添加了，而又有一部分没有被加到，所以要重新排序，防止失序
    }
    else {
        for (int i = L[p]; i <= R[p] ; i ++)
        if(x <= r[i].id && r[i].id  <= R[p])r[i].data+=k;
        sort(r+L[p],r+R[p]+1,cmp);
        for (int i = L[q]; i <= R[q] ; i ++)
        if(L[q] <= r[i].id && r[i].id <= y)r[i].data+=k;
        sort(r+L[q],r+R[q]+1,cmp);//每次处理零散的块都要排序
        for (int i = p + 1; i <= q - 1 ; i ++)
        add[i]+=k;//整段直接维护就好了
    }
    return 0;
}

 队列分块入门三：

这道题和上面的题目基本类似，就是长度为n的序列进行操作，n个操作，每次要求实现区间加法以及查询【l，r】中x的前驱（即小于x的最大的数）

 

然后无赖的我把上面的代码改了改，然后就过了。。。但是很慢，现在在想怎么优化一下

贴上（用不要脸的手段）AC的代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, m, t = 0;
struct node {
    int data, id;
} r[200005];
int L[100005], R[100005], block, pos[200005], add[200005];
int cmp(node A, node B) { return A.data < B.data; }

int change(int x, int y, int k);
int query(int x, int y, int k);
signed main() {
    cin >> n;
    m = n;
    for (int i = 1; i <= n; i++) cin >> r[i].data, r[i].id = i;
    block = (int)(sqrt(n));
    while (R[t] != n) {
        t++, L[t] = (t - 1) * block + 1;
        R[t] = min(t * block, n);
    }
    for (int i = 1; i <= t; i++) {
        for (int j = L[i]; j <= R[i]; j++) pos[j] = i, add[i] = 0;
        sort(r + L[i], r + R[i] + 1, cmp);
    }
    for (int i = 1; i <= m; i++) {
        int op, x, y, k;
        cin >> op >> x >> y >> k;
        if (op == 0)
            change(x, y, k);
        else
            cout << query(x, y, k) << endl;
    }
    return 0;
}
int find(int x, int y, int num, int ttt) {
    int s = x, mm = y;
    while (x < y) {
        int mid = (x + y) >> 1;
        if (r[mid].data + add[ttt] < num)
            x = mid + 1;
        else
            y = mid - 1;
    }
    while (r[x].data + add[ttt] >= num && x >= s) x--;
    if (r[x].data + add[ttt] >= num)
        return -1;
    return r[x].data + add[ttt];
}
int query(int x, int y, int k) {
    int p = pos[x], q = pos[y];
    if (pos[x] == pos[y]) {
        int M = -1;
        for (int i = L[p]; i <= R[p]; i++)
            if (x <= r[i].id && r[i].id <= y && r[i].data + add[p] < k)
                M = max(M, r[i].data + add[p]);
        return M;
    } else {
        int M = -1;
        for (int i = L[p]; i <= R[p]; i++)
            if (x <= r[i].id && r[i].id <= R[p] && r[i].data + add[p] < k)
                M = max(M, r[i].data + add[p]);
        for (int i = L[q]; i <= R[q]; i++)
            if (L[q] <= r[i].id && r[i].id <= y && r[i].data + add[q] < k)
                M = max(M, r[i].data + add[q]);
        for (int i = p + 1; i <= q - 1; i++) M = max(M, find(L[i], R[i], k, i));
        return M;
    }
}
int change(int x, int y, int k) {
    int p = pos[x], q = pos[y];
    if (pos[x] == pos[y]) {
        for (int i = L[p]; i <= R[p]; i++)
            if (x <= r[i].id && r[i].id <= y)
                r[i].data += k;
        sort(r + L[p], r + R[p] + 1, cmp);
    } else {
        for (int i = L[p]; i <= R[p]; i++)
            if (x <= r[i].id && r[i].id <= R[p])
                r[i].data += k;
        sort(r + L[p], r + R[p] + 1, cmp);
        for (int i = L[q]; i <= R[q]; i++)
            if (L[q] <= r[i].id && r[i].id <= y)
                r[i].data += k;
        sort(r + L[q], r + R[q] + 1, cmp);
        for (int i = p + 1; i <= q - 1; i++) add[i] += k;
    }
    return 0;
}

至于正解还在想。

莫队

这是个基于分块的算法，它不支持修改，但是支持区间查询，因此是强制离线的（当然可以有办法把它搞成在线啦）。它的应用很广例如下面的题目：

一个颜色序列，长度为n，现在要统计区间内颜色的总数，给出m个询问，每次查询区间【l，r】。 n、m ∈(1,10^5]

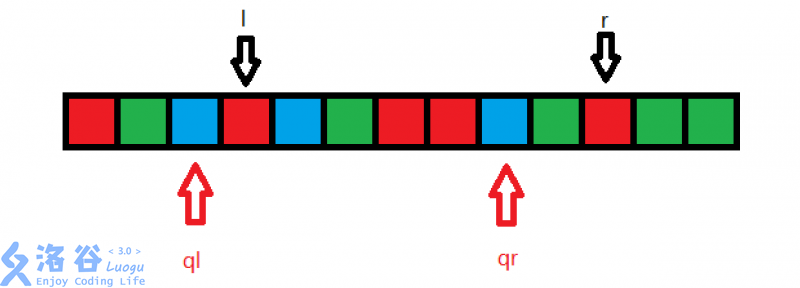
运用双指针法，每次移动指针必然会导致一种颜色减少，一种颜色变多，每次移动都会影响算法时间复杂度，所以我们要尽量减少移动的次数

那么， 排序它不香吗？

问题来了，我们要怎么排序？？

开篇提过，这是个基于分块的算法，所以我们还是采用分块的思想，把每个询问的l以及r分别属于哪一个块给求出来，按照l属于的块作为第一关键字排序，r属于的块作为第二关键字排序，如果两个询问的l、r都属于同一个块，再按l作为第三关键字，r作为第四关键字 （要是还相等那也没办法）

然后就可以愉快的暴力了！直接移动ql和qr指针就可以了呀！