8-bit Optimizers via Block-wise Quantization
概
本文提出了一种 8-bit 的优化器, 其主要贡献算是 block-wise 的量化 (从我的角度看一点也不 novel)?
8-bit Optimizers
-
对于 k-bit 量化, 就是找到一个 qmap:
\[\mathbf{Q}^{\text{map}}: [0, 2^k - 1] \rightarrow D, \]通常 \(D = [-1/0, 1]\).
-
然后, 对于输入向量 \(\mathbf{T} \in \mathbb{R}^n\), 首先是将它 normalize 到区域 \(D\) 上, 比如对于 \(D = [-1, 1]\), 可以:
\[\mathbf{T} / \max(|\mathbf{T}|) \in [-1, 1]. \] -
然后, 我们可以得到 \(\mathbf{T}\) 的量化结果:
\[\mathbf{T}_i^Q = \mathop{\text{argmin}} \limits_{j=0}^{2^k - 1} \bigg|\frac{\mathbf{T}_i}{\max(|\mathbf{T}|)} - \mathbf{Q}^{\text{map}}(j) \bigg|. \] -
反量化则可以通过如下方式得到:
\[\mathbf{T}_i^D = \mathbf{Q}^{\text{map}}(\mathbf{T}_i^Q) \cdot \max(|\mathbf{T}|). \] -
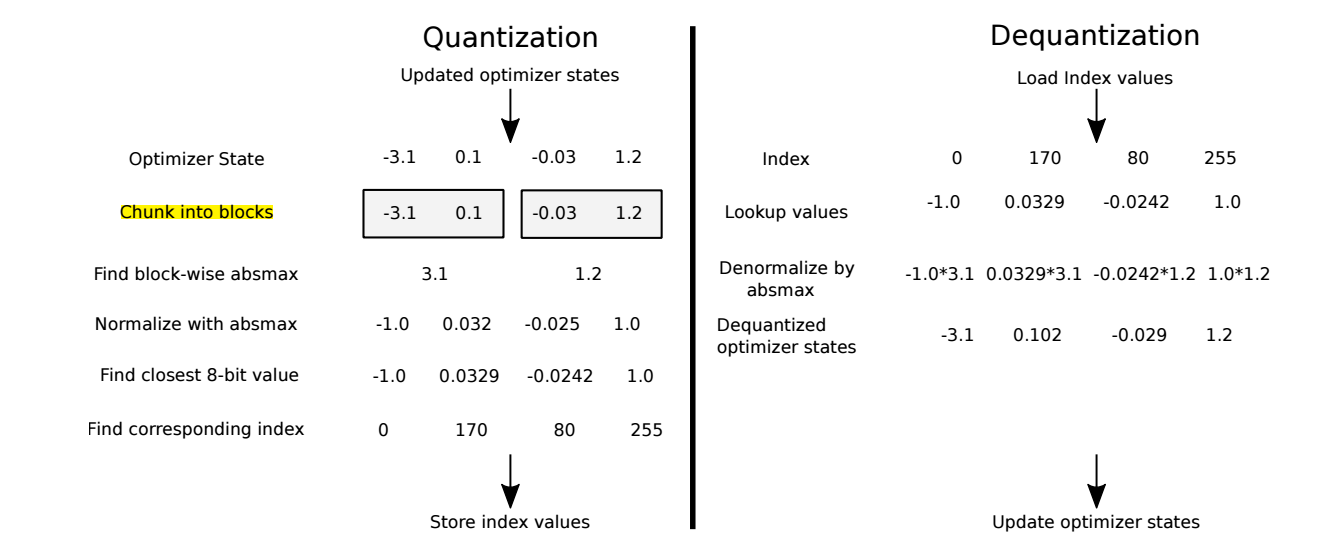
但是呢, 作者发现这种方式在优化器中不太稳定, 所以采用了一种 block-wise 的形式. 对于长度为 \(n\) 的 tensor (如果是多维的就拉成向量), 设定 block-size 为 B (作者推荐 B=2048), 则就有:
\[\lceil n / B \rceil \]个 blocks.
注: 在实际实现中, 可能需要补零.
-
于是对于每个 block 中的元素, 量化过程如下:
\[\mathbf{T}_{bi}^Q = \mathop{\text{argmin}} \limits_{j=0}^{2^k - 1} \bigg|\frac{\mathbf{T}_{bi}}{\max(|\mathbf{T}_b|)} - \mathbf{Q}^{\text{map}}(j) \bigg|, \\ b = 0, 1, \ldots, \lceil n / B \rceil - 1, \quad i = 0, 1, \ldots, B - 1. \] -
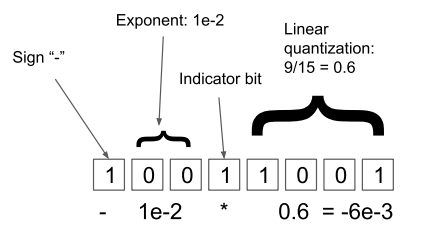
具体的, 作者采用的是 dynamic tree quantization 方法:
- 第一个 bit 表示符号, 记为 \(s\);
- 第二个开始直到第一个 '1' 出现开始, 为指数项, 假设总共有 \(E\) 个 bits;
- 接着都是分数项目, 假设所表示的数为 \(f\).
-
于是最后的数字为:
\[s \cdot 10^{-E} \cdot f. \]
-
好处是, 由于 exponent 项 和 分数项的 bits 是可以随意调动的, 所以实际上我们可以针对每个数字进行分配. 从而实现大数小数都近似的不错的效果.
-
不过作者还是选择固定 fraction (分数) 项, 因为他实际观察发现 Adam 的缓存的状态通常差距就在 3-5 orders.
-
此外, 作者还提出了 stable embedding layer: 在加入位置编码前, 先用一次 layer normalization.
注: 显然, 不论是 block-wise 量化还是 stable embedding layer 都是为了缩小所要量化对象的数值范围, 从而保证结果的一致. 很不优雅.
