Uncertainty of Thoughts: Uncertainty-Aware Planning Enhances Information Seeking in Large Language Models

目录

• 概
• UoT
• 代码

Hu Z., Liu C., Feng X., Zhao Y., Ng S., Luu A. T., He J., Koh P. W. and Hooi B. Uncertainty of thoughts: Uncertainty-aware planning enhances information seeking in large language models. NeurIPS, 2024.

概

通过判断问题所导致的不确定性降低程度来衡量一个问题的重要性.

UoT

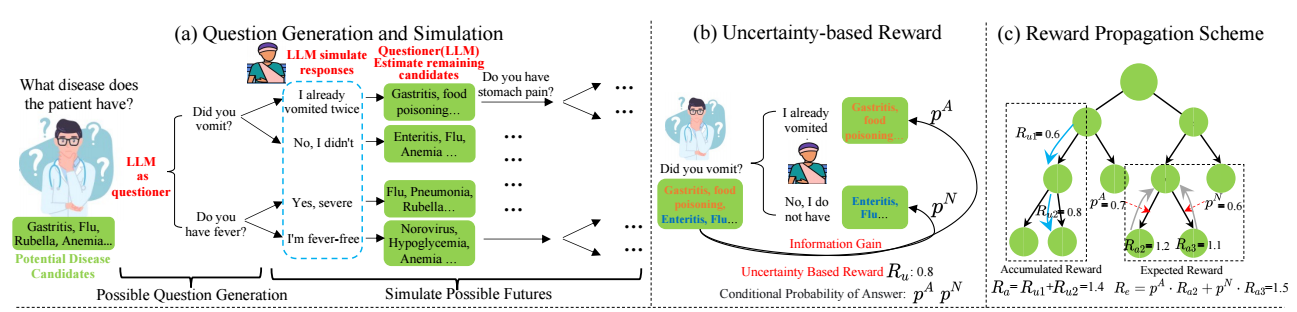
• 如上图 (a) 所示, 为了判断一个病人的具体病症, 我们可以通过多种 "问题链" 来实现. 当然了, 我们希望问题链能尽可能地问更少的问题, 增加诊断的效率.

• 假设在用户解答问题 $q$ 前, 有 $\Omega$ 种可能的病症, 对于具体的回答:

  • 'Yes' (肯定回答): 导致可能的病症蜕变为 $\Omega^Y$;
  • 'No' (否定回答): 导致可能的病症蜕变为 $\Omega^N$.

• 一个有效率的问题应当尽可能使得 $|\Omega^Y| = |\Omega^N|$ (我们假设 $\Omega^Y \cap \Omega^N = \empty$) 以实现最大限度地不确定性的降低.

• 让我们定量地看一看, 假设 $\Omega = \{\omega_i\}$ 中每个病症的概率为 $p(\omega_i)$ (通常, 取 $p(\omega_i) = 1 / |\Omega|$, 但有些时候, 或许我们会给每个病症设定不同的先验, 毕竟每个病症出现的概率是不一样的), 此时当前的不确定性可以有如下的信息熵度量:

  $$H(\Omega) = -\sum_{i} p(\omega_i) \log p(\omega_i).$$

• 现在, 由于问题 $q$, $\Omega = \Omega^Y \cap \Omega^N$, 我们有:

  $$p(\omega|\Omega^Y) = p(\omega) / \sum_{\omega \sim \Omega^Y} p(\omega'), \\ p(\omega|\Omega^N) = p(\omega) / \sum_{\omega \sim \Omega^N} p(\omega').$$

• 对于两个 subset, 我们有:

  $$H(\Omega^Y) = -\sum_{i: w_i \in \Omega^Y} p(\omega_i|\Omega^Y) \log p(\omega_i|\Omega^Y), \\ H(\Omega^N) = -\sum_{i: w_i \in \Omega^N} p(\omega_i|\Omega^N) \log p(\omega_i|\Omega^N).$$

• 由此, 我们可以计算问题 $q$ 所对应的条件熵:

  $$H(\Omega|q, a) = - p(a = yes) H(\Omega^Y) - p(a = no) H(\Omega^N),$$

  而且

  $$p(a = yes) = p(\Omega^Y), \quad p(a = no) = p(\Omega^N).$$

• 于是, 作者采用问题 $q$ 前后的信息熵的变化作为不确定性的降低程度 (实际上是互信息):

  $$IG(\Omega) := H(\Omega) - H(\Omega|q, a).$$

• 这个只是一个问题 $q$ 的度量. 实际上, 作者让 LLM:

  1. 提出 $m$ 个问题, 并设想 $m$ 个问题分别给出肯定和否定答案后, 所对应的 $\Omega$ 的变化;
  2. 对于每个 subset, 重复 $1$.

• 如此一来, 我们会有一个树状的结构, 一个好的问题, 不仅要求它对于接下来的不确定性分割是最优的, 而对于后续的也是如此的. 所以作者额外设计了 reward propagation 机制:

  • Accumulated Reward:

    $$R_a(v) := R_u(v) + \left \{ \begin{array}{ll} 0 & v \text{ is } root \\ R_a(\text{Parent}(v)) & \text{otherwise}. \end{array} \right .$$

  • Expected Reward:

    $$R_a(v) := \left \{ \begin{array}{ll} R_a(v) & \text{if } v \text{ is a leaf; otherwise:} \\ p_v^Y R_e(v^Y) + p_v^N R_e(v^N) & \text{if } v \text{ is an Answerer Node}; \\ \frac{1}{m} \sum_{w \in \text{Children}(v)}^m R_e(w) & \text{if } v \text{ is a Questioner Node}. \end{array} \right .$$

代码

[official-code]