Modularity-based Graph Clustering

概
符号说明
Modularity
代码

[1] Newman M. E. J. and GirvanM. Finding and evaluating community structure in networks. Physical review E, 2004.

[2] Newman M. E. J. Fast algorithm for detecting community structure in networks. Physical Review E, 2004.

[3] Blondel V. D>, Guillaume J., Lambiotte R. and Lefebvre E. Fast unfolding of communities in large networks. JSTAT, 2008.

[4] Shiokawa H., Fujiwara Y. and Onizuka M. Fast algorithm for modularity-based graph clustering. AAAI, 2013.

[5] Arai J., Shiokawa H., Yamamuro T., Onizuka M. and Iwamura S. Rabbit order: Just-in-time parallel reordering for fast graph analysis. IPOPS, 2016.

概

介绍一类基于 modularity 指标的 graph 的聚类方法.

符号说明

$\mathcal{G} = (\mathcal{V}, \mathcal{E})$ , 图;
$\mathcal{G}_k = (\mathcal{V}_k, \mathcal{E}_k), \mathcal{E}_k := \{(v_i, v_j) \in \mathcal{E}| v_i, v_j \in \mathcal{V}_k\}$ , 子图;

注: 这里讨论的边 $(v_i, v_j)$ 是有向的, 无向图可以扩展成 $(v_i, v_j), (v_j, v_i)$ 同时存在即可.

Modularity

我们的目标是将图 $\mathcal{G}$ 切分成 $K$ 个子图, 而且我们希望子图之内的点关系紧密, 子图和子图之间尽可能关系不那么紧密.
首先, 我们需要定义一个指标来形式化这一点.
- 假设我们已经有了一个划分, 得到了 $K$ 个子图, 由此我们可以计算:
  $e_{ij} = \frac{ |\{(v, v') \in \mathcal{E}| v \in \mathcal{V}_i, v' \in \mathcal{V}_j\}| }{ |\mathcal{E}| }$
  为子图 $i$ 到子图 $j$ 的边的数量占全部边的比重.
- 接着我们可以计算行和:
  $a_i = \sum_{j=1}^K e_{ij},$
  为子图 $\mathcal{G}_i$ 到所有点的连边占所有边的一个比重.
由此, 我们可以定义如下指标来刻画子图分化的优劣 (越大越好):

$Q = \sum_{i} (e_{ii} - a_i^2).$
让我们来理解下这么设计的原因:
- 假设 $\mathcal{G}$ 是一个随机图, 任意两个节点都有 $p > 0$ 的概率相连.
- 容易证明, 此时对于任意两个不交的子图 $\mathcal{G}_i, \mathcal{G}_j$ , 我们有:
  $e_{ij} = \frac{ |\mathcal{V}_i| |\mathcal{V}_j| p }{ |\mathcal{V}|^2 p } = \frac{ |\mathcal{V}_i| |\mathcal{V}_j| }{ |\mathcal{V}|^2 }.$
  于是
  $a_{i} = \sum_{j=1}^K e_{ij} = \frac{ |\mathcal{V}_i| \sum_{j} |\mathcal{V}_j| }{ |\mathcal{V}|^2 } = \frac{|\mathcal{V}_i|}{|\mathcal{V}|}.$
- 于是, 当 $\mathcal{G}$ 为随机图的时候, 我们有
  $e_{ij} = a_i a_j \rightarrow e_{ii} = a_i^2.$
- 于是 $Q\approx 0$ 表明实际上整个图是趋向于随即图的, 反之 $Q$ 变大的时候, 里随机图越远.
让我们进一步分析 $Q$ . 令 $E = [e_{ij}] \in \mathbb{R}^{K \times K}$ . 我们有

$Q = \text{Tr}(E) - \|E\|_F^2,$
若 $e_{ij} = e_{ji}$ ( $E$ 对称):

$Q = \text{Tr}(E) - \|E\|_F^2 = \sum_{k=1}^K \lambda_k - \sum_{k=1}^K \lambda_k^2,$
容易证明, 在 $\lambda_k = 1 / K$ 的时候取得最大值. 即:

$e_{ij} = \left \{ \begin{array}{ll} \frac{1}{K} & i = j \\ 0 & i \not= j \end{array} \right ..$
换言之, 这个目前会带一点均匀分割的倾向.

Agglomerative Hierarchical Clustering

既然如此, 我们可以以这个指标为导向, 每个节点一开始作为独立的类别, 然后逐步地选择能够最大化 $Q$ 的合并方式聚类.
假设, 我们要将 $\mathcal{G}_i, \mathcal{G}_j$ 合并, 则合并前后的 $Q$ 的变化值为:

$\Delta Q = \underbrace{e_{ii} + e_{ij} + e_{jj} - (a_i + a_j)^2}_{i \cup j} - \underbrace{[e_{ii} - a_i^2]}_i - \underbrace{[e_{jj} - a_j^2]}_j = 2(e_{ij} - a_i a_j).$

Louvain

Louvain 算法其实也大差不大:

特别地, 在 networkx 的实现以及后续的方法的提及中, 都是引入 resolution $\gamma > 0$ 的指标:

$Q = \sum_{i} (e_{ii} - \gamma \cdot a_i^2).$
$\gamma$ 越大, 则最后的结果容易产生越多的类, 反之类别数目越少.
仅凭此公式可能有点难以理解, 实际上, 我们有:

$\Delta Q = 2(e_{ij} - \gamma \cdot a_i a_j).$
显然, $\Delta Q$ 是随着 $\gamma$ 增大而减小的, 因此, 原本可以合并的节点 $i, j$ 可能随着 $\gamma$ 的增加而导致 $\Delta Q < 0$ 而不能合并. 合并的机会降低自然会导致最后类别数目的增加.

Modularity-based Graph Clustering

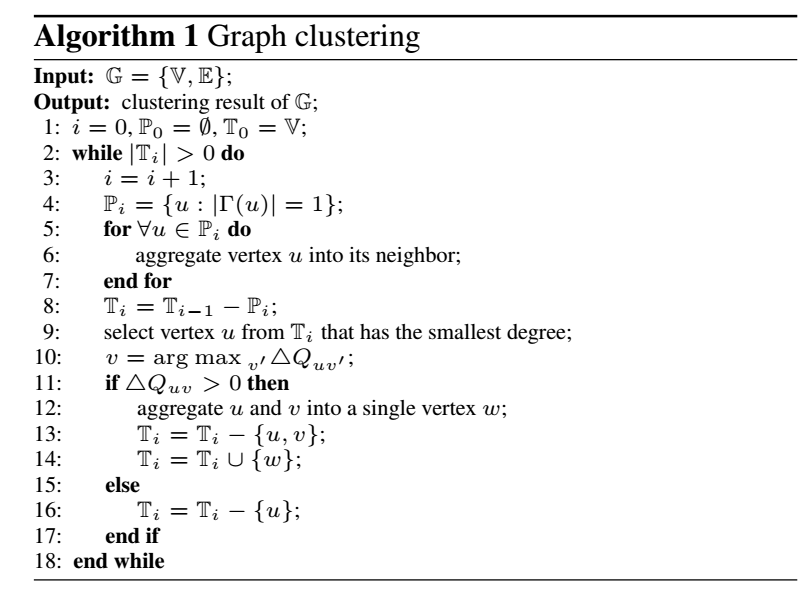
这篇文章, 也是直接以 modularity 为目标进行的. 与之前的算法相比, 主要多了一个 pruning 过程.
注意到, 每次合并前, 首先统计:

$\mathbb{P}_i = \{u: |\Gamma (u)| = 1\},$
即邻居个数为 $1$ 的节点, 然后直接将这些节点融入他们的邻居之中. 这是因为, 这种情况下:

$e_{ij} = a_i.$
注意, 这里 $\Gamma(u) := \{v \in \mathbb{T}_i: (u, v) \in \mathcal{E}_i\}$ . 此外, 如果 $u$ 本身是一个 cluster, 那就没法加入到 $\mathbb{P}_i$ 中了.
另一个有意思的点是, 每一次合并前, 作者挑选的是具有最小 degree 的点, 这确保每次比较的次数是比较少的.
另外, 一旦发现 $\Delta Q_{uv} \le 0, v = \arg\max_{v'} \Delta Q_{uv'}$ , 则直接把 $u$ 从 $\mathbb{T}_i$ 中剔除. 这是因为 (可以通过归纳法证明), 一旦在某一次出现与周围邻居均有 $\Delta Q_{uv} \le 0, v \in \Gamma(u)$ 的情况, 即使经过多轮聚类之后, 依然如此.