优化与收敛率小记

目录

概

近来对优化和收敛速度有了一些新的感悟, 特此一记. 这些感悟有的来自博客 (如 here), 有的来自书籍. 以往只是套一些收敛的模板, 这里我会讲一下如何从几何的角度去理解这些收敛性.

基本的设定

  • 假设我们希望优化:

    (1)minx∈Rdf(x),

    可行域这里就暂不讨论了.

  • 我们采取最一般的梯度下降:

    xt+1=xt−η∇f(x),

    其中 η>0 是学习率, ∇f(x)∈Rd 为 f 关于 x 的梯度.

非凸优化

  • 基本的条件 (L-smooth):

    (C.1)f(y)−f(x)−⟨∇f(x),y−x⟩≤L2‖y−x‖22,L>0

  • 我们来看看 L-smooth 这个条件实际上为我们带来的是啥:

    (2)f(xt+1)−f(xt)≤⟨∇f(xt),xt+1−xt⟩+L2‖xt+1−xt‖22=⟨∇f(xt),−η∇f(xt)⟩+Lη2‖∇f(xt)‖22=(Lη22−η)⏟αη‖∇f(xt)‖22.

  • 倘若我们希望收敛速度尽可能快, 那么一个贪心的方法就是每一步的下降都尽可能多, 即我们应当尽可能使得 (3) 的右边项小于 0 的同时进一步变小, 这等价于约束我们的迭代步长:

    1. 根据 αη 可知, 当 η=1/L 的时候近似会有一个'最优'的迭代步长;
    2. 退而求其次, 我们也应当确保 η∈(0,2/L) 以确保

      f(xt+1)<f(xt).

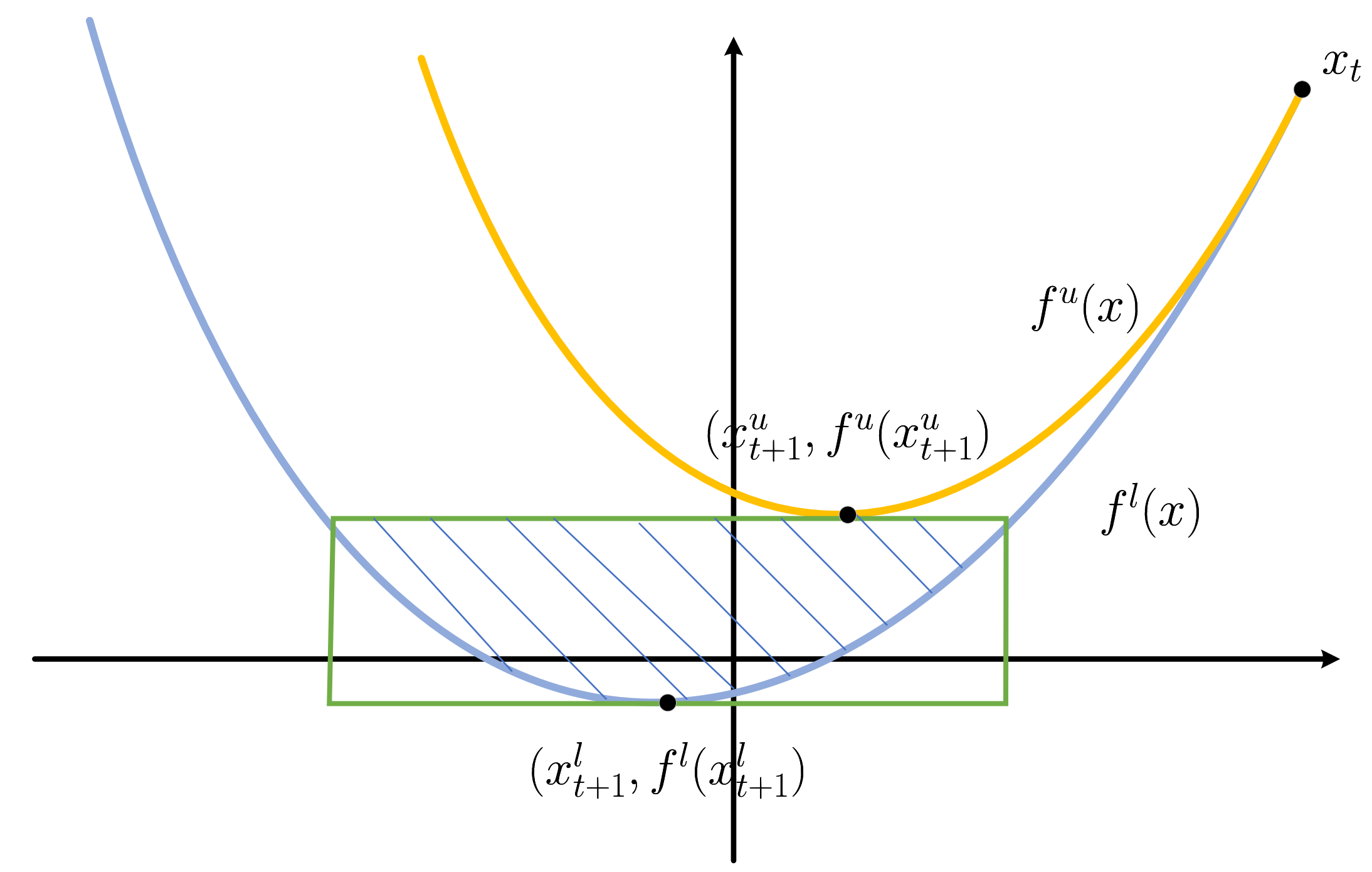
  • 我们可以几何上去理解 L-smooth, 定义:

    fu(x)=f(xt)+⟨∇f(xt),x−xt⟩+L2‖x−xt‖22,

    由于

    f(x)≤fu(x)

    故而 L-smooth 实际上是用一个抛物线为 f(x) 定义了一个上界. 而

    xt+1u=xt−1L∇f(xt)

    就是这个抛物线的最低点, 所以 η=1/L 是沿着这条抛物线下降的最优路线.

  • 真正的最优点 (x∗,f(x∗)) 的区域, 其实是在上图的蓝色画线区域内, 当然了, 由于没有其它条件, 我们既无法 bound 住 f(xt)−f(x∗), 更无法 bound 住 ‖xt−x∗‖, 后面当我们引入更多的条件的时候, 我们可以获得更多更好的性质.

  • 所以, 我们来证明一个不坏的收敛性:

    f(xt+1)−f(xt)≤αη‖∇f(xt)‖22⇒∑t=0T−1(f(xt+1)−f(xt))≤αη∑t=0T−1‖∇f(xt)‖22⇒∑t=0T−1‖∇f(xt)‖22≤1αη∑t=0T−1(f(xt+1)−f(xt))←αη<0, if η∈(0,2/L)⇒mint=0,…,T−1⁡‖∇f(xt)‖22≤1T∑t=0T−1‖∇f(xt)‖22≤1αηT∑t=0T−1(f(xt+1)−f(xt))⇒mint=0,…,T−1⁡‖∇f(xt)‖22≤1−αηT(f(x0)−f(xT))≤1−αηT(f(x0)−f(x∗))⇒mint=0,…,T−1⁡‖∇f(xt)‖22≤2(2η−Lη2)T(f(x0)−f(x∗)).

    当 η 取 1/L, 左边项可以被

    O(2LT)

    bound 住.

凸优化

  • 除了 L-smooth 条件 (C.1) 外, 凸优化额外引入:

    (C.2)f(y)≥f(x)+⟨∇f(x),y−x⟩.

  • 它的用处是什么呢? 我们依旧通过几何的方式去理解:

    fl(x)≤f(x)≤fu(x),

    其中

    fl(x):=f(xt)+⟨∇f(xt),x−xt⟩.

  • 相比较普通的 L-smooth 而言, 凸优化实际上是为函数 f(x) 设定了一个下界, 这使得 (x∗,f(x∗)) 所在的区域 (蓝色划线部分) 进一步缩小.

  • 首先, 对于一般的函数, 我们都有:

    ‖xt+1−x∗‖22=‖xt−η∇f(xt)−x∗‖22=‖xt−x∗‖22−2η⟨∇f(xt),xt−x∗⏟fl(xt)−fl(x∗)⟩+η2‖∇f(xt)‖22,

    于是:

    fl(xt)−fl(x∗)=η2‖∇f(xt)‖22+12η(‖xt−x∗‖22−‖xt+1−x∗‖22).

  • 于是, 我们有:

    f(xt+1)−f(x∗)≤fu(xt+1)−f(x∗)=(fl(xt)−f(x∗))−(fl(xt)−fu(xt+1))≤(fl(xt)−fl(x∗))−(fu(xt)−fu(xt+1))=(fl(xt)−fl(x∗))+αη‖∇f(xt)‖22≤12η(‖xt−x∗‖22−‖xt+1−x∗‖22)+(αη+η2)‖∇f(xt)‖22

    当我们假定 η∈(0,1/L), 有 αη+η2<0 可得

    f(xt+1)−f(x∗)≤12η(‖xt−x∗‖22−‖xt+1−x∗‖22)⇒∑t=1T−1f(xt+1)−f(x∗)≤12η(‖x0−x∗‖22−‖xT−x∗‖22)⇒1T∑t=1T−1f(xt+1)−f(x∗)≤12ηT(‖x0−x∗‖22−‖xT−x∗‖22)⇒f(xt+1)−f(x∗)≤1T∑t=1T−1f(xt+1)−f(x∗)≤12ηT(‖x0−x∗‖22−‖xT−x∗‖22)⇒f(xt+1)−f(x∗)≤12ηT(‖x0−x∗‖22−‖xT−x∗‖22)≤‖x0−x∗‖222ηT.

    倒数第二步成立是因为 f(xt),t=0,… 是递减的 (η∈(0,1/L) 保证了这一点).

强凸优化

  • 强凸函数是 (C.2+) 的一个增强版:

    (C.2+)σ2‖y−x‖22≤f(y)−f(x)−⟨∇f(x),y−x⟩,σ>0.

注: σ=0 时 f 为凸函数.

  • 实际上, 若 f 的 Hessian 矩阵满足 σ≤λmin(H)≤λmax(H)≤L, 就可以很自然地推导出上面的不等式. 于是乎, 我们常常会听闻条件数 κ=L/σ 对于收敛速率的影响, 通常 κ→1 收敛速度越快.

  • 现在的问题是, L-smooth 这个条件 (C.1) 能够保证我们每一次迭代都有 f(xt+1)<f(xt), 那 (C.2) 这种对于左边的控制于收敛有什么帮助?

    f(xt+1)−f(xt)≥⟨∇f(xt),xt+1−xt⟩+σ2‖xt+1−xt‖22≥⟨∇f(xt),−η∇f(xt)⟩+ση22‖∇f(xt)‖22≥(ση22−η)⏟βη‖∇f(xt)‖22.

注: η∈(0,2/σ)⊃(0,2/L) 能够保证 βη 是负的.

  • 于是, 我们可以证明:

    (ση22−η)⏟βη‖∇f(xt)‖22≤f(xt+1)−f(xt)≤(Lη22−η)⏟αη‖∇f(xt)‖22.

  • 倘若, 我们沿着之前的思路分析, 容易发现 βη 会随着 σ→L 而增大 (绝对值 |βη| 减小), 也就是说, 当 σ⇒ 的时候,

    f(xt+1)−f(xt)

    的下降的最大可能幅度是在减小的. 这实在不符合我们的预期, 如果按照这种思路分析, 正当的结论应该是 σ→L 收敛性变差才对.

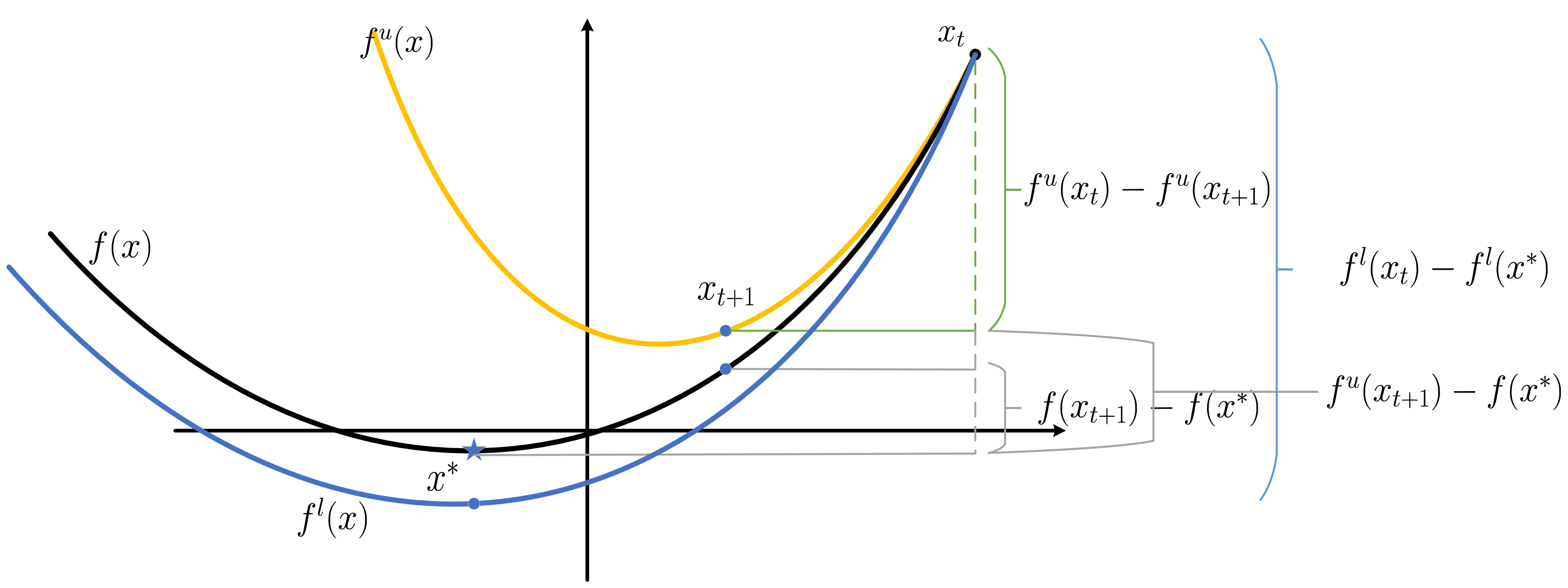
  • 这里, 我们修改下之前 fl 的定义:

    fu(x)=f(xt)+⟨∇f(xt),x−xt⟩+L2‖x−xt‖22,fl(x)=f(xt)+⟨∇f(xt),x−xt⟩+σ2‖x−xt‖22.

    我们有:

    1. fl(x)≤f(x)≤fu(x), 所以最小值点 x∗ 比在二者的中间区域;
    2. 我们可以进一步压缩 (x∗,f(x∗)) 可能的所在区域, 实际上在上图的绿色框框内部 (更准确的是画线区域):

      fl(xt+1l)≤f(x∗)≤fu(xt+1u),xt+1l=xt−1σ∇f(xt)⇒f(xt+1l)=f(xt)−12σ‖∇f(xt)‖22,xt+1u=xt−1L∇f(xt)⇒f(xt+1u)=f(xt)−12L‖∇f(xt)‖22.

      此外, x∗ 所在区域为:

      x∗∈{x∈Rd:‖x−xt+1σ∇f(xt)‖22≤L−σLσ2‖∇f(xt)‖22}=:St.

      这是以 xt−1σ∇f(xt) 为圆心, L−σLσ2‖∇f(xt)‖2 为半径的球内.
    3. 由此, 我们可以进一步得到 (xt,f(xt)) 与 (x∗,f(x∗)) 的关系:

      12L‖∇f(xt)‖22≤f(xt)−f(x∗)≤12σ‖∇f(xt)‖22,1σ(1−L−σL)‖∇f(xt)‖2≤‖xt−x∗‖2≤1σ(1+L−σL)‖∇f(xt)‖2,

      所以, 当 σ→L 的时候, f(xt)−f(x∗) 可容易接近, 同时 xt 与 x∗ 的距离可能越小.

  • 总而言之, σ>0 的作用其实是告诉我们这个强凸函数的 (x∗,f(x∗)) 可以被限制在一个区域里面, 倘若 σ=0, 实际上 fu 的之下的区域都是有可能, 自然就不会有上述的性质, 自然收敛性会差一点.

  • ok, 接下来, 让我们具体地证明一下收敛性, 令 η∈(0,1/L), 于是我们有 (根据图示了然):

    f(xt+1)−f(xt)≤αη‖∇f(xt)‖22⇔f(xt+1)−f(x∗)≤f(xt)−f(x∗)+αη‖∇f(xt)‖22⇔f(xt+1)−f(x∗)≤f(xt)−f(x∗)+2αησ(f(xt)−f(x∗))⇔f(xt+1)−f(x∗)≤(1+2αησ)(f(xt)−f(x∗))⇔f(xT)−f(x∗)≤(1+2αησ)T(f(x0)−f(x∗))⇔f(xT)−f(x∗)≤(1+σ(Lη2−η))T(f(x0)−f(x∗)).

    由于 1+σ(Lη2−η)<1, 我们便证明了收敛性 (而且是很强的收敛性).

注: 我们也可以模仿凸优化里的收敛性证明来证明一个稍差的收敛性:

  • 可以发现:

    f(xt+1)−f(x∗)≤fu(xt+1)−f(x∗)=(fl(xt)−f(x∗))−(fl(xt)−fu(xt+1))≤(fl(xt)−fl(x∗))−(fu(xt)−fu(xt+1))=(fl(xt)−fl(x∗))+αη‖∇f(xt)‖22≤12η(‖xt−x∗‖22−‖xt+1−x∗‖22)−σ2‖xt−x∗‖22+(αη+η2)‖∇f(xt)‖22

    其中, 最后一步略有不同之处, 因为这里 fl 是原来的直线加上一个二次项.

  • 于是, 当 ηt≤1tσ 且 ηt<2/L 时我们有:

    f(xt+1)−f(x∗)≤12ηt(‖xt−x∗‖22−‖xt+1−x∗‖22)−σ2‖xt−x∗‖22⏟≤0+(αηt+ηt2)‖∇f(xt)‖22⇒f(xt+1)−f(x∗)≤(αηt+ηt2)‖∇f(xt)‖22⇒f(xt+1)−f(x∗)≤ηt2‖∇f(xt)‖22⇒∑t=1T(f(xt+1)−f(x∗))≤∑t=1Tηt2‖∇f(xt)‖22⇒∑t=1T(f(xt+1)−f(x∗))≤∑t=1TηtL2⇒∑t=1T(f(xt+1)−f(x∗))≤L2σ∑t=1T1t⇒∑t=1T(f(xt+1)−f(x∗))≤L2σ(1+ln⁡T)⇒f(xT+1)−f(x∗)≤1T∑t=1T(f(xt+1)−f(x∗))≤L2σ(1+ln⁡T)T.

  • 在特殊的情况下 (σ/L>8/9), 我们可以证明, ‖xt−x∗‖2 也是单调下降的:

    ‖xt+1−x∗‖2≤21σL−σL‖∇f(xt)‖2←xt+1∈St≤21σL−σLσ1−L−σL‖xt−x∗‖2←x∗∈St=21LL−σ−1‖xt−x∗‖2<‖xt−x∗‖2←σ/L>8/9.

    这也进一步说明了 σ→L 的重要性.

注: 我本来想证明一般情况下也有这个性质来着, 但是似乎是困难的, 因为仅凭画图我们就可以做出 x∗ 位于 xt,xt+1 之间的情况. 所以我感觉除非上述条件成立 (即区域非常小), 不然很难保证 ‖xt−x∗‖2 是恒下降的. 当然了, 或许我们能够通过约束 xt+1 的范围来保证这一点. 比如, 我们取

xt+1←xt−1−L−σLσa∇f(xt),

此时 xt+1 恰在 xt 在 St 的投影上, 所以必有:

‖xt+1−x∗‖2≤‖xt−x∗‖2.

但是, 想要设计一个算法近似这种应该是很难的吧.

posted @   馒头and花卷  阅读(114)  评论(0)  编辑  收藏  举报
相关博文：
· Convergence of Adam Under Relaxed Assumptions
· Regularized Stochastic Learning and Online Optimization
· 无条件凸优化问题
· 梯度下降法的两个收敛性证明
· 优化算法-3.梯度下降
阅读排行：
· Manus重磅发布：全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后，我竟然真的恢复了删除的微信聊天记录！
· 没有Manus邀请码？试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
历史上的今天：
2023-07-18 REALM Retrieval-Augmented Language Model Pre-Training
2023-07-18 Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks
点击右上角即可分享
微信分享提示