An Attentive Inductive Bias for Sequential Recommendation beyond the Self-Attention
概
本文在 attention block 中引入高低频滤波.
符号说明
-
\(\mathcal{U}\), users;
-
\(\mathcal{V}\), items;
-
\(\mathcal{S}^u = [v_1^u, v_2^u, \ldots, v_{|\mathcal{S}^u|}^u]\), sequence;
-
\(\mathbf{E}_{\mathcal{S}^u} \in \mathbb{R}^{L \times d}\), sequence embeddings;
-
attention matrix:
\[\mathbf{A} = \text{softmax}( \frac{ \mathbf{Q} \mathbf{K}^T }{ \sqrt{d} } ), \quad \mathbf{Q} = \mathbf{E}_{\mathcal{S}^u} \mathbf{W}_Q, \: \mathbf{K} = \mathbf{E}_{\mathcal{S}^u} \mathbf{W}_K. \] -
\(\bm{f}_j = [e^{2\pi \mathbf{i} (j-1) \cdot 0}, \ldots, e^{2\pi \mathbf{i} (j - 1)(N-1)}]^T / \sqrt{N} \in \mathbb{R}^N\), 维 DFT (Discrete Fourier Transform) 的第 \(j\) 个基底, 这里 \(\mathbf{i}\) 表示 imaginary unit.
BSARec (Beyond Self-Attention for Sequential Recommendation)
-
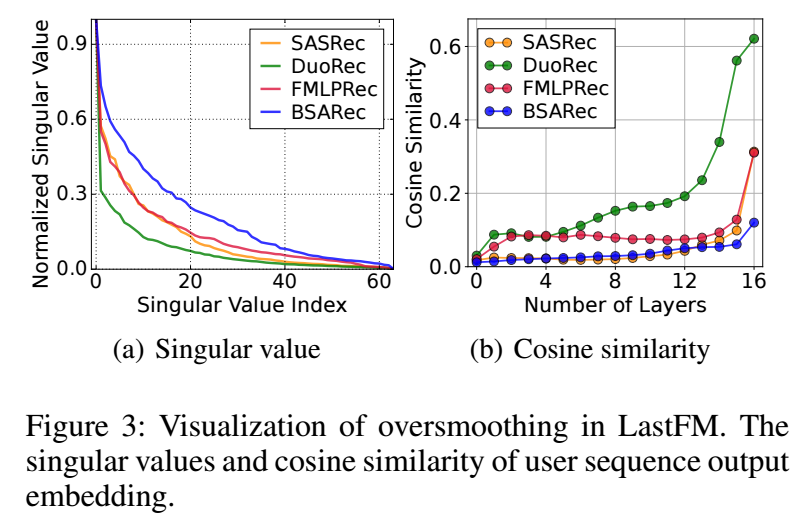
首先, 作者对一般的序列推荐模型如 SASRec, FMLPRec 的演进过程中的 embedding 的奇异值变化和 user embedding 的 cosine similarity 进行比较, 可以发现 embedding 主特征值的主导地位相当明显, 而且随着层数的加深, 越发变得相似. 故而, 作者得出结论, 认为现在的主流的序列推荐模型主要是在学习一个 low-pass 的滤波.
-
令 DFT 的基底矩阵为 \(\mathcal{F}\), 对于任意的向量 \(\bm{x}\) 我们可以得到它的频域上的表示
\[\bar{\bm{x}} = \mathcal{F} \bm{x}. \]并令 \(\bar{\bm{x}}_{lfc} \in \mathbb{C}^c\) 表示 \(\bar{\bm{x}}\) 的最低频位置的 \(c\) 个元素, \(\bar{\bm{x}}_{hfc} \in \mathbb{C}^{d-c}\) 表示 \(\bar{\bm{x}}\) 的最高频位置的 \(d-c\) 个元素.
-
由此, 我们可以通过 Inverse DFT 得到
- \(\bm{x}\) 的低频信号:\[\text{LFC} [\bm{x}] = [\bm{f}_1, \bm{f}_2, \ldots, \bm{f}_c] \bar{\bm{x}}_{lfc} \in \mathbb{R}^d. \]
- \(\bm{x}\) 的高频信号:\[\text{HFC} [\bm{x}] = [\bm{f}_{c+1}, \bm{f}_{c+2}, \ldots, \bm{f}_d] \bar{\bm{x}}_{hfc} \in \mathbb{R}^d. \]
- \(\bm{x}\) 的低频信号:
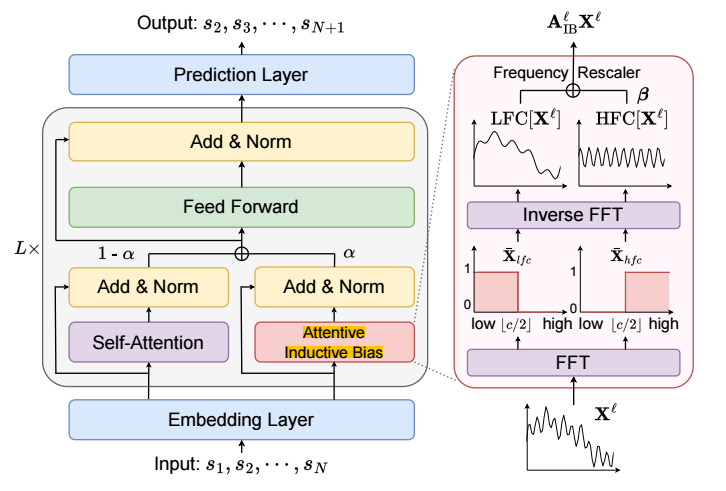
- 令 \(\mathbf{X}^{\ell}\) 表示第 \(l\) 层的输入, 则 attention 后的结果为\[\alpha \mathbf{A}_{\text{IB}}^{\ell} \mathbf{X}^{\ell} + (1 - \alpha) \mathbf{A}^{\ell} \mathbf{X}^{\ell}. \]其中 \(\mathbf{A}^{\ell} \mathbf{X}^{\ell}\) 对应正常的 attention 机制, 而 \(\mathbf{A}_{\text{IB}}^{\ell} \mathbf{X}^{\ell}\) 则\[\mathbf{A}_{\text{IB}}^{\ell} \mathbf{X}^{\ell} = \text{LFC}[\mathbf{X}^{\ell}] + \bm{\beta} \text{HFC}[\mathbf{X}^{\ell}], \]其中 \(\bm{\beta}\) 是可训练的参数, 它可以是每个维度设置一个, 也可以不同维度共享一个 (代码里的是这种方案).
代码
[official]
