Hungry Hungry Hippos: Towards Language Modeling with State Space Models

目录

• 概
• H3
• 代码

Fu D. Y., Dao T., Saab K. K., Thomas A. W., Rudra A. and Re C. Hungry hungry hippos: towards language modeling with state space models. 2022.

概

Mamba 系列第五作: H3.

H3

• 感觉 H3 是之前的 linear attention 和 SSM 的一个结合, 它所做的只是把 linear attention 中的部件改成了 SSM 的结构.

• attention 的平方复杂度一直是一个问题, 给定 $Q_i, K_i, V_i \in \mathbb{R}^d, i=1,\ldots, N$ ($N$ 为序列长度), linear attention 解决这个问题的思路是:

  $$O_i = \frac{ \sum_{j=1}^i \text{Sim}(Q_i, K_j) V_j }{ \sum_{j=1}^i \text{Sim} (Q_i, K_j) } \in \mathbb{R}^d,$$

  其中对于一般的 softmax attention, $\text{Sim}(q, k) = e^{q^T k}$, linear attention 则是

  $$\text{Sim} (q, k) = \phi(q)^T \phi(k),$$

  $\phi$ 是某个 non-linear function.

• 由此一来, 我们就会有:

  $$O_i = \frac{ \phi(Q_i)^T \sum_{j=1}^i \phi(K_j) V_j^T }{ \phi(Q_i)^T \sum_{j=1}^i \phi (K_j) },$$

  令

  $$S_i = \sum_{j=1}^i \phi (K_j) V_j^T \in \mathbb{R}^{d \times d}, \\ z_i = \sum_{j=1}^i \phi (K_j) \in \mathbb{R}^d, \\ d_i = \phi (Q_i)^T z_i \in \mathbb{R}.$$

  我们有

  $$O_i = \frac{\phi(Q_i)^T S_i}{d_i}.$$

• H3 就是把:

  $$\phi (\mathbf{K}) \rightarrow \text{SSM}_{\text{shift}} (\mathbf{K}) \odot \mathbf{V}, \\ S_i \rightarrow \text{SSM}_{\text{diag}} ( \text{SSM}_{\text{shift}} (\mathbf{K}) \odot \mathbf{V}), \\ $$

  最后我们有

  $$\mathbf{O} = \mathbf{Q} \odot \text{SSM}_{\text{diag}} ( \text{SSM}_{\text{shift}} (\mathbf{K}) \odot \mathbf{V}).$$

• 模型结构如下:

• 算法如下:

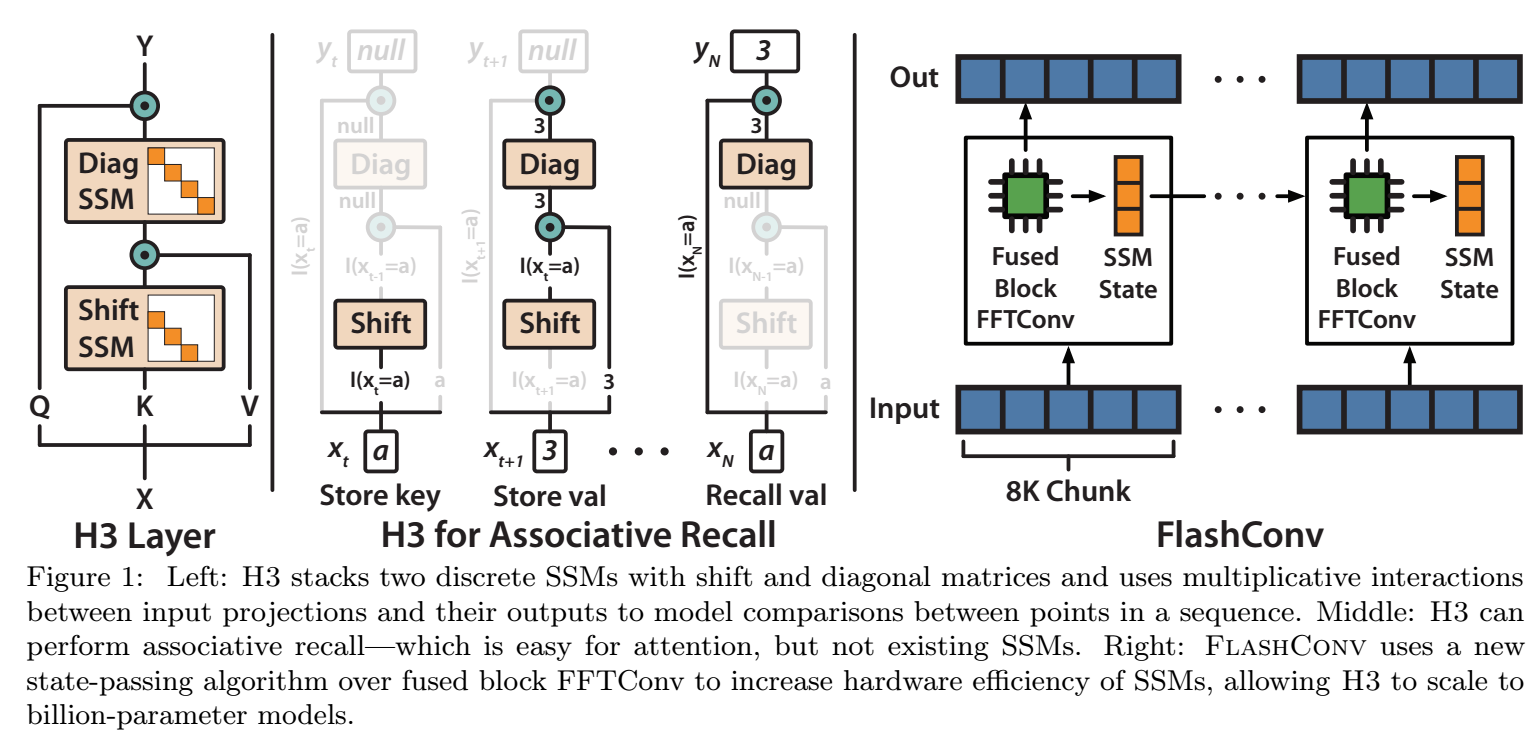
注: 作者额外讨论了加速算法, 感兴趣的请回看原文.

代码

[official-code]