Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers
概
Mamba 系列的第二作: LSSL.
符号说明
- \(u(t) \in \mathbb{R}\), 输入信号;
- \(x(t) \in \mathbb{R}^N\), 中间状态;
- \(y(t) \in \mathbb{R}\), 输出信号
LSSL
-
从 LSSL 开始, 作者开始围绕 linear system 做文章:
\[\tag{1} \dot{x}(t) = A x(t) + B u(t), \\ y(t) = C x(t) + Du(t), \]注意, 这里作者把 \(A, B, C, D\) 简化为和时间 \(t\) 无关的量, 且仅仅讨论的是一维的信号.
-
采用 generalized bilinear transform (GBT) 可以将上述的 ODE 离散化:
\[x_t = \bar{A} x_{t-1} + \bar{B} u_t, \\ y_t = C x_t + D u_t, \]其中
\[\bar{A} = (I - \alpha \Delta t \cdot A)^{-1} (I + (1 - \alpha) \Delta t \cdot A), \\ \bar{B} = \Delta t (I - \alpha \Delta t \cdot A)^{-1} B, \]\(\Delta t\) 是时间间隔, 而 \(\alpha\) 是一个 bilinear 的超参数. 具体的推导可以见 here.
-
我们现在仅关注 \(x_t\), 然后看看一个具体的例子. 取 \(A=-1, B=1, \alpha=1, \Delta t = \exp(z)\), 我们有
\[x_t = \frac{1}{1 + \exp(z)} x_{t-1} + \frac{\exp(z)}{1 + \exp(z)} u_t = (1 - \sigma(z)) x_{t-1} + \sigma(z) u_t. \]这实际上就是一个 gating 机制 (常常用在 RNN 的更新上).
-
ok, 对于 RNN, 我们可以把其中的一层看出是对 (1) 的一次近似, 那么多层的效果是什么? 作者认为这和 Picard iteration 有关系, Picard iteration, 即
\[x_{i+1}(t) := x_i (t_0) + \int_{t_0}^t f(s, x_i(s)) ds \]可以证明随着 \(i\) 的增加, 会逐步收敛到真实解, 换言之, 多层的叠加可以让误差越来越小.
-
Deep LSSLs:
- LSSLs 的具体构造就是上述离散过程的叠加, 同时不同 block 之间添加 skip connection 和 layer norm.
- 假设我们的输入信号是 \(\mathbb{R}^{L \times H}\) 的, 其中 \(L\) 表示序列长度, \(H\) 是维度, 此时信号不是 1 维的. 作者的做法是, 为每个维度单独设立:
\[A \in \mathbb{R}^{N \times N}, \quad B \in \mathbb{R}^{N \times 1}, \quad C \in \mathbb{R}^{1 \times N}, \quad D \in \mathbb{R}, \quad \Delta t \in \mathbb{R} \]分别进行上述的离散过程. 此外, 这里需要注意的是, \(\Delta t\) 我们也是可学习的.
- 作者还提到, 输出信号 \(y(t)\) 不一定必须是 1 维的, 也可以是 \(M\) 维的, 此时 \(C \in \mathbb{R}^{M \times N}, D \in \mathbb{R}^{M \times 1}\). 这会导致最后的输出维度是 \(H\cdot M\), 可以通过 MLP 映射回 \(H\).
所以总共的参数量为:
\[HNN + HN1 + HMN + HM + H + HMH = \mathcal{O}(HN^2 + HMN + H^2M). \]
注: 作者好像把 LSSL 的代码删掉了, 不过我注意到后续的 S4 的设定里面, 是为每个维度单独设立 \(A, B, C, D\) 还是共享是可以选择的 (也可以是部分维度共享, 取决于 n_ssm 这个参数).
注: \(A\) 的初始化应用 HiPPO.
和其它方法的联系
-
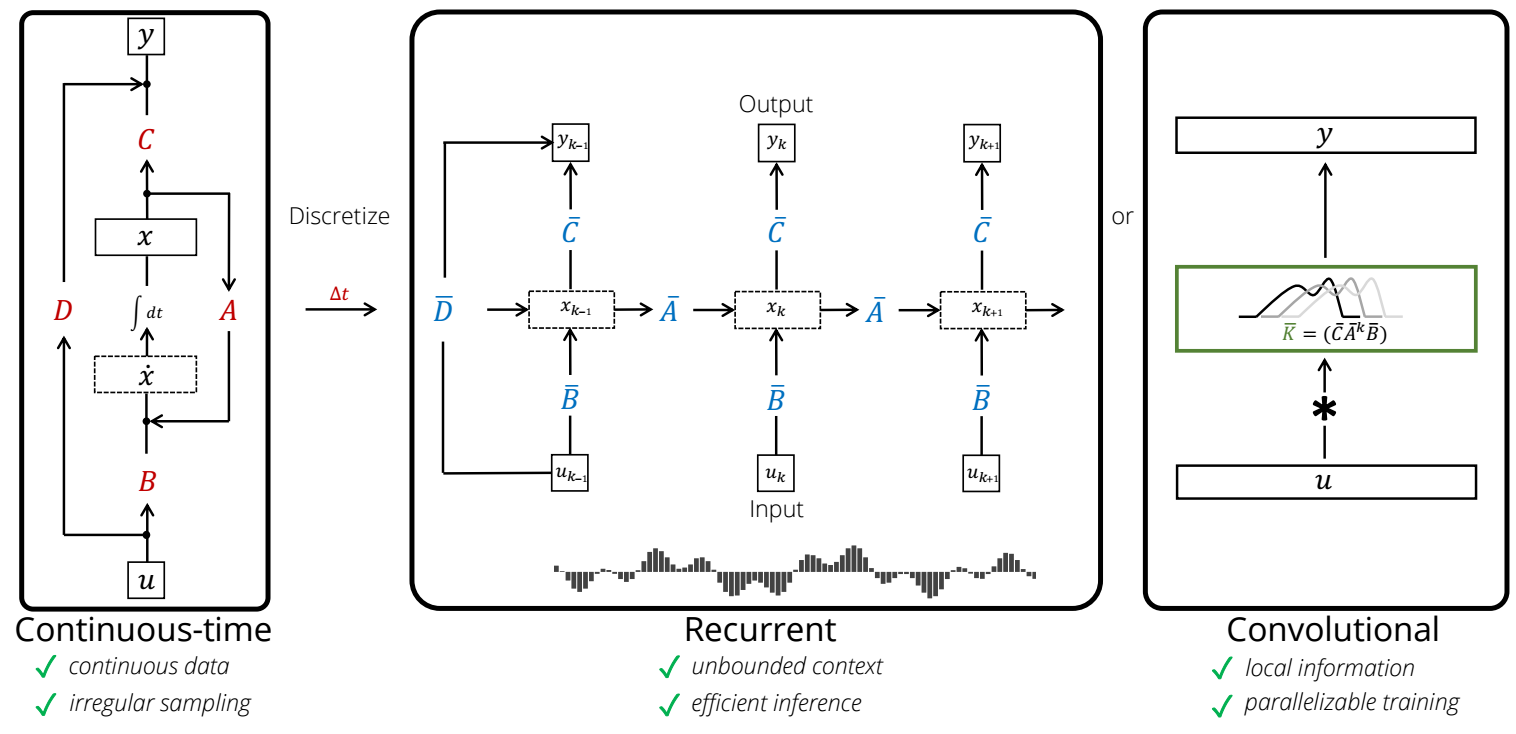
LSSL 除了可以看成是 RNN 外, 实际上还具有卷积的特性, 容易发现:
\[\begin{array}{ll} y_k &= C(\bar{A})^k \bar{B} u_0 + C (\bar{A})^{k-1} \bar{B} u_1 + \cdots + C \overline{AB} u_{k-1} + \bar{B} u_k + D u_k \\ &= \sum_{s} C(\bar{A})^{k-s} u_s \\ \end{array}, \]故
\[y = \mathcal{K}_L (\bar{A}, \bar{B}, C) * u + Du. \]其中
\[\mathcal{K}_L (A, B, C) := (CB, CAB, \ldots, CA^{L-1}B). \] -
所以, LSSL 具有卷积的优点, 可以并行计算.
