Further Generalizations of the Jaccard Index
Costa L. Further generalizations of the jaccard index. 2021.
概
本文介绍了 Jaccard Index (Jaccard Similarity), 和它的一些变种.
Jaccard Index
-
对于两个普通的集合 \(A, B\), 它们的 Jaccard Index 为
\[J(A, B) = \frac{ |A \cap B| }{ |A \cup B| } = \frac{ |A \cap B| }{ |A| + |B| - |A \cap B| }. \] -
Jaccard Index 对于大部分的 \(A, B\) 的相对关系都能确定出来, 但是也有例外:
-
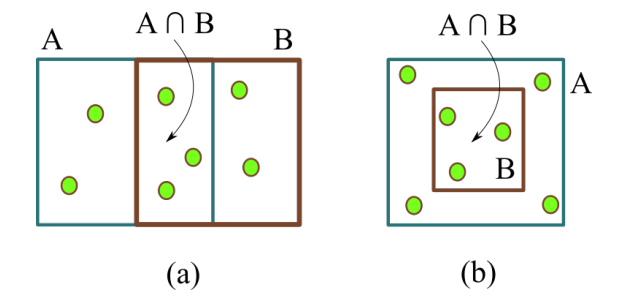
上图 (a), (b) 两种情况的 Jaccard Index 都是 \(3 / 7\), 但是其实表达的是两种不同的状态, 为了进一步区分它, 我们引入 Interiority (也成 overlap, homogeneity):
\[\mathcal{I}(A, B) = \frac{ |A \cap B| }{ \min \{ |A|, |B| \} }. \] -
容易证明
\[0 \le \mathcal{I}(A, B) \le \mathcal{J}(A, B) \le 1. \] -
进一步地, 我们可以定义 Coincidence:
\[\mathcal{C}(A, B) = \sqrt{ \mathcal{J}(A, B), \mathcal{I}(A, B) }. \]
推广到 multisets
-
multisets 值得是集合的每个元素还附带其出现次数, 如
\[A = \{ (x_1, a_1), (x_2, a_2), \ldots, (x_N, a_N) \}, \\ B = \{ (x_1, b_1), (x_2, b_2), \ldots, (x_N, b_N) \}, \]其中 \((a, b)\) 代表各自的出现次数.
-
接着, 我们可以定义二者的 Jaccard Index:
\[\mathcal{J}_M (A, B) = \frac{ \sum_{i=1}^N \min (a_i, b_i) }{ \sum_{i=1}^N \max (a_i, b_i). } \]其实, 容易发现, \(a_i, b_i\) 不必是非负整数, 可以很容易推广到 \(\mathbb{R}_+\).
-
对于 Interiority 和 Coincidence 可以类似地进行推广.
推广到 Multiple sets
-
Jacarrd Index:
\[\mathcal{J} (A_1, \ldots, A_K) = \frac{ |\bigcap_{k=1}^K A_k| }{ |\bigcup_{k=1}^K A_k| }. \] -
Interiority index:
\[\mathcal{I}_{[K, i]} (A_1, \ldots, A_k) = \frac{ |\bigcap_{k=1}^K A_k| }{ |X_i| }, \]其中 \(X_i\) 表示第 \(i\) 小的 集合.
