Outrageously Large Neural Networks The Sparsely-Gated Mixture-of-Experts Layer

目录

• 概
• MoE
  • 训练

Shazeer N., Mirhoseini A., Maziarz K., Davis A., Le Q., Hinton G. and Dean J. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. ICLR, 2017.

概

Mixture-of-Experts (MoE).

MoE

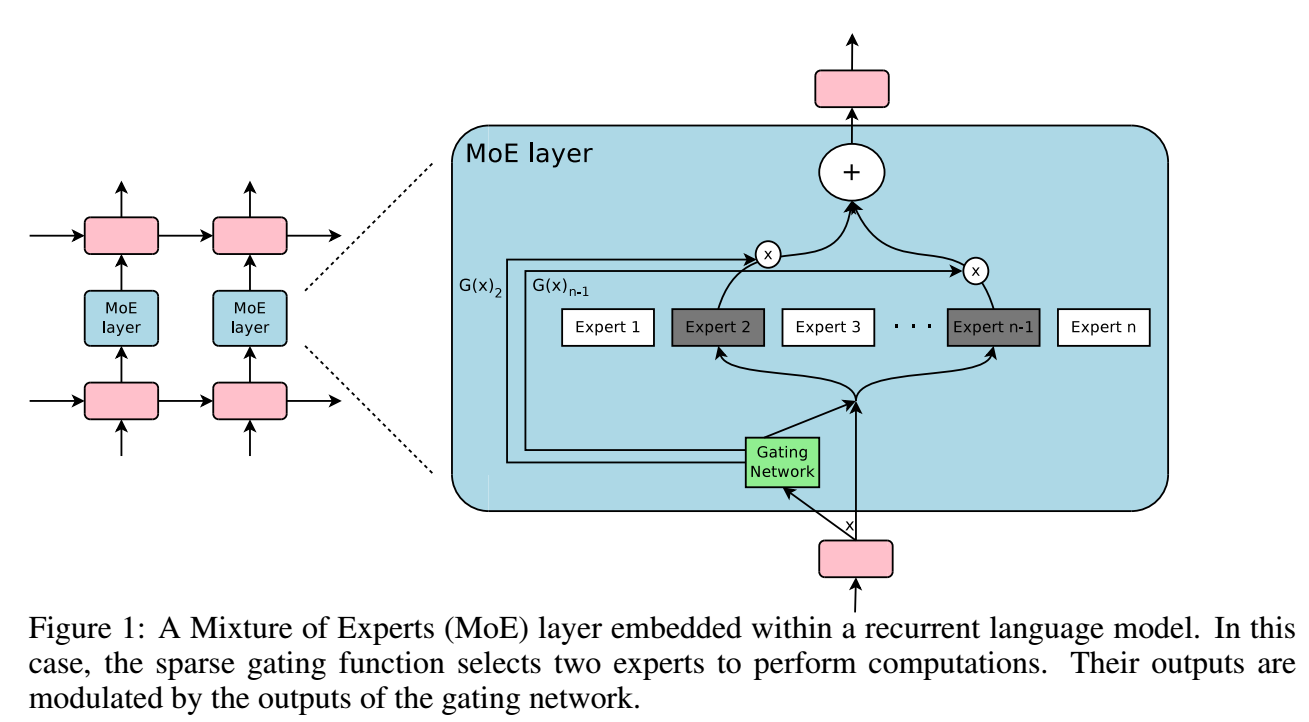
• 通过一 gating network 选择不同的 expert:

  $$y = \sum_{i=1}^n G(x)_i E_i(x),$$

  若 $G(x)_i = 0$, 则我们不需要计算 $E_i(x)$.

• $E_i(x)$ 可以是任意的网络, 所以现在的问题主要是如何设计 $G$. 倘若我们希望选择 $k$ 给 experts, 可以:

  $$G(x) = \text{Softmax}( \text{KeepTopK}(H(x), k), ) \\ H(x)_i = (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{noise})_i), \\ \text{KeepTopK}(v, k)_i = \left \{ \begin{array}{ll} v_i & \text{if } v_i \text{ is in the top} k \text{ elements of } v. \\ -\infty & \text{otherwise}. \end{array} \right .$$

• 特别的是, 这里加了高斯噪声, 并用 $W_{noise}$ 去调节不同位置的噪声的比重, 从而可以实现负载平衡 (?).

训练

• 如果不对 $G$ 加以额外的限制, 容易出现某些 experts 持续获得较大的权重, 所以本文引入了一个 soft constraint

  $$L_{importance}(X) = w_{importance} \cdot CV(Importance (X))^2, \\ Importance(X) = \sum_{x \in X} G(x)$$

  CV 作者说是 variation, 是方差吗?

• 有了 soft constraint, 依然会出现每个 expert 接受的样本数量的差别很大 (有些 expert $i$ 可能会接受很少的样本但是其上 $G(x)_i$ 都很大, 有些 expert $i$ 可能接受很多的样本, 但是其上 $G(x)i$ 都很小). 所以作者额外添加了对于选择概率的约束.

• 对于样本 $x$, expert $i$ 被选择的概率为 (感觉这个定义应该是有问题的)

  $$P(x, i) = Pr\bigg( (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{noise})_i) > kth_excluding (H(x), k, i) \bigg).$$

  其中 $kth_excluding(v, k, i)$ 表示 $v$ 中的 k-th 大的值 (排除 $i$).

• 所以,

  $$P(x, i) = \Phi( \frac{(x \cdot W_g)_i - kth_excluding(H(x), k, i)}{ \text{Softplus}((x \cdot W_{noise})_i) } ).$$

• 定义

  $$Load(X)_i = \sum_{x \in X} P(x, i),$$

  则

  $$L_{load}(X) = w_{load} \cdot \text{CV}(Load(X))^2.$$