Embedding Whitening
概
Whitening 用于将各向异性 (anisotropic) 的 sentence embeddings 转换成各向同性的 setence embeddings, 从而 sentence 间的相似度能够被正确估计.
主要内容
BERT-Flow
-
在 [1] 之前, 利用 BERT 将各层的 (e.g., 最后一层或者最后两层的) embeddings 取平均作为一个句子的表示, 但是这种简单的方式效果并没有那么理想.
-
[1] 中的作者首先分析认为, BERT 应该是有能力捕获句子和句子间的相关度的, 那么是为什么导致这个现象的发生呢?
-
作者认为, 这是因为通过极大似然学到的 word embeddings 是各向异性的, 在实际中, word embeddings 构成一个锥型空间:
- Word frequency biases the embedding space: 出现频率越高的 word 距离原点越近, 反之越远 (下图的第一栏);
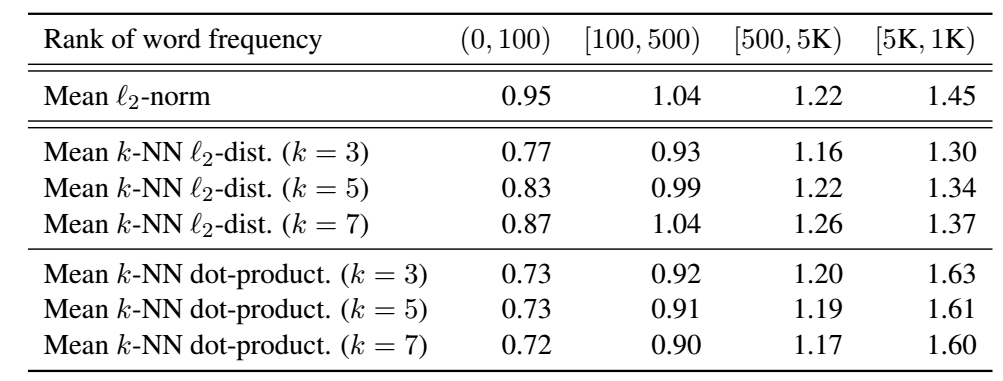
2. **Low-frequency words disperse sparsely:** 频率越低的 word 分散的越稀疏 (上图的中间栏), 这导致低频的 word 的点出现了很多 'holes', 导致整个分布不是凸的 (意会).
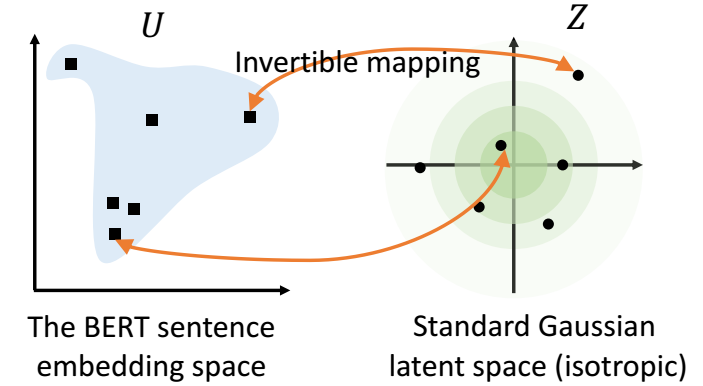
- 上面的 word embedding 的问题就会导致 sentence embeddings 难以准确的建模 sentence 间的相关度. BERT-flow 就是希望将 sentence embeddings 进行一个转换 (形如):
-
做法就是对于任意的 sentence embedding \(\mathbf{u}\), 设计一个可逆函数 \(f_{\phi}\), 通过
\[\mathbf{z} = f_{\phi}^{-1}(\mathbf{u}) \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \]映射到标准正态分布中去, 根据分布和可逆函数的性质, 我们得到:
\[p_{\mathcal{U}}(\mathbf{u}) = p_{\mathcal{Z}} (f_{\phi}^{-1} (\mathbf{u})) | \text{det} \frac{ \partial f_{\phi}^{-1}(\mathbf{u}) }{ \partial \mathbf{u} }|, \]这里 \(p_{\mathcal{Z}}\) 为标准正态分布.
-
然后通过极大似然优化 \(\phi\)
\[\max_{\phi} \mathbb{E}_{ \mathbf{u} = \text{BERT(sentence)}, \text{sentence} \sim \mathcal{D} } \log p_{\mathcal{Z}} (f_{\phi}^{-1}(\mathbf{u})) + \log | \text{det} \frac{ \partial f_{\phi}^{-1}(\mathbf{u}) }{ \partial \mathbf{u} }|. \] -
这个, 我说实话, 感觉和 normalizing flow 也有出入 .
-
于是乎, 新得到的 Z 就是服从标准正态分布了, 也就各向同性了.
BERT-Whitening
-
[2] 采取了一种更加简便的方法. 作者希望找到 \(\mathbf{\mu} \in \mathbb{R}^d\) 和矩阵 \(W \in \mathbb{R}^{d \times d}\), 使得
\[\tilde{\mathbf{x}}_i = (\mathbf{x}_i - \mu) W, \quad i=1,2,\ldots, N \]服从各项同性的, 即协方差矩阵
\[\tilde{\Sigma} = \frac{1}{N} \sum_{i=1}^N \tilde{\mathbf{x}}_i \tilde{\mathbf{x}}^T = I. \]显然的是, \(\mu = \frac{1}{N} \sum_{i=1}^N \mathbf{x}_i\).
-
现在我们需要找到一个矩阵 \(W\) 满足
\[W^T \Sigma W = I, \\ \Sigma = \frac{1}{N} \sum_{i=1}^N (\mathbf{x}_i - \mu) (\mathbf{x} - \mu)^T. \] -
注意到, \(\Sigma\) 是半正定矩阵, 于是我们有
\[\Sigma = V\Lambda V^T, \]若我们令 \(W = V \Lambda^{-1/2}\), 就有
\[W^T \Sigma W = I. \] -
于是, 最后的 whitening 的 embedding 为
\[(\mathbf{x} - \mu) V \Lambda^{-1/2}. \] -
ok, 让我们进一步看看它做了啥, 假设
\[X - \mu = U\Lambda^{1/2}V^T, \]所以最后的
\[(X - \mu) V \Lambda^{-1/2} = U. \] -
如果决定维度太高, 可以选择 \(U\) 的前 \(k\) 列.

