Lightweight Modality Adaptation to Sequential Recommendation via Correlation Supervision

目录

• 概
• 符号说明
• Motivation
• Knowledge Distillation framework for modality-enriched Sequential Recommenders (KGSR)
  • 相似度建模
  • 相似度预测
  • 训练

Hu H., Liu Q., Li C. and Kan M. Lightweight modality adaptation to sequential recommendation via correlation supervision. ECIR, 2024.

概

解决多模态序列推荐中的 modality forgetting 问题.

符号说明

• $v$, 结点;
• $a$, 模态特征;
• $\mathbf{m}_a$, 模态特征通过 encoder 得到的 embedding;
• $\mathbf{e}_a$, 通过 embedding initialization module 得到的 embedding;
• $\mathbf{e}_v$, 随机初始化的 id embedding;

Motivation

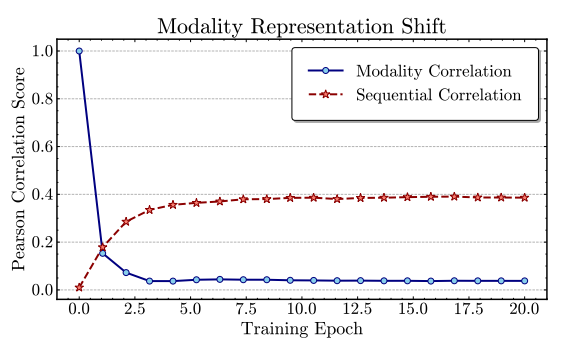
• 同一个序列模型, 使用 item 的模态信息作为表示和利用随机初始化的 ID embedding 进行训练, 二者随着训练的进行, 他们间的 Pearson score 如上图蓝色线所示, 可以发现, 一下子就降到了 0 附近. 这意味着模态信息在训练过程中被遗忘了.

注: 我不清楚模态信息是怎么被完全遗忘的? 因为维度不一样, 不能直接作为初始化吧. 难不成简单用 MLP 降维就能起到这个效果?

Knowledge Distillation framework for modality-enriched Sequential Recommenders (KGSR)

• 作者解决上面的问题的思想和简单, 就是希望 embedding 在训练过程中, 尽可能保持原先模态特征的相关性.

相似度建模

• 首先计算原先模态的相似度:

  1. 将原先 encoder 得到的模态 embedding $\mathbf{m}_a$ 通过一个自编码进行去噪:
     $$\mathbf{ \tilde{m} }_a = \text{AE} (\mathbf{m}_a).$$

  2. 通过 correlation scoring function 计算两两的相似度
     $$\xi (\mathbf{\tilde{m}}_i, \mathbf{\tilde{m}}_j) \rightarrow r_{ij}.$$

• codebook 编码. 上面的模态相似度比较粗粒度, 这里作者额外采用一种更为复杂的方式. 它就是采用向量量化, 把两个模态的相似度隐射为一个类别 $c_{ij} \in [1, 2, \ldots, x]$. 可以认为每个类别代表 $i, j$ 在哪个层面是相似的. 我们希望后续的训练的 embedding 能够预测出这些类别.

相似度预测

• 接下来, 对于可训练的 embedding $\mathbf{e}_{a_i}, \mathbf{e}_{a_j}$, 我们将上面的得到的相似度约束加在其中.

• 对于粗粒度的相似度:

  1. 计算
     $$\hat{r}_{ij} = \xi (g_{\phi} (\mathbf{e}_{a_i}), g_{\phi} (\mathbf{e}_{a_j})).$$

  2. 计算损失:
     $$\mathcal{L}_S^{KD} = \frac{1}{N^2} \sum_{i=1,j=1}^{N, N} (\sigma(r_{ij}/ \tau) - \sigma(\hat{r}_{ij} / \tau))^2,$$
     其中 $\tau$ 为 temperature parameter 用于条件 match 的程度.

• 对于类别的相似度:

  1. 计算每个类别的概率

     $$p = W_{out}(ReLU)(W_c (\tilde{e}_{ij})), \\ \tilde{e}_{ij} = |\mathbf{e}_{a_i} - \mathbf{e}_{a_j}| \in \mathbb{R}^d,$$

     其中 $W_c \in \mathbb{R}^{d \times d}, W_{out} \in \mathbb{R}^{d \times x}$.

  2. 计算损失:

     $$\mathcal{L}_{C}^{KD} = -\frac{1}{N^2} \sum_{i=1,j=1}^{N, N} \sum_{t=1}^x \mathbb{I}(c_{ij} = t) \log (p_{ij, t}).$$

训练

• 最后的训练目标就是
  $$\mathcal{L} = \mathcal{L}^{RS}(y, \hat{y}) + \lambda_1 \mathcal{L}_S^{KD} + \lambda_2 \mathcal{L}_C^{KD}.$$