A Revisiting Study of Appropriate Offline Evaluation for Top-N Recommendation Algorithms
概
系统性的讨论了推荐指标, 数据集切分, 优化方式对推荐系统离线评估的影响.
实验设置
-
数据集:
-
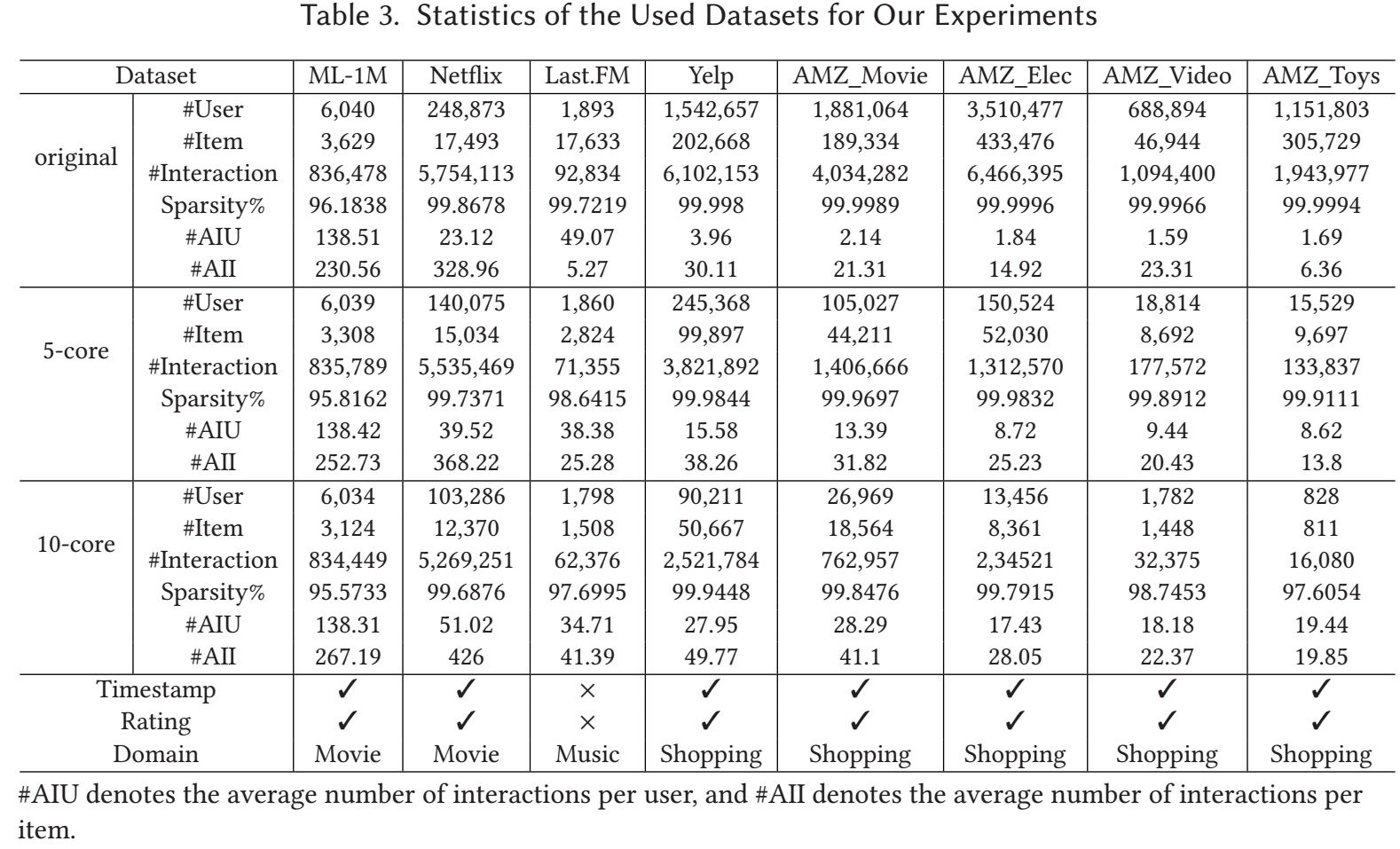
推荐算法:
- 传统算法: Popularity, ItemKNN;
- 矩阵分解: SVD++, BPRMF, NCF;
- Item similarity-based: Factored Item Similarity Model (FISM), Neural Attentive Item Similarity Model (NAIS);
- GNN-based: NGCF, LightGCN;
- Non-sampling algorithms: CDAE, MultiVAE, ENMF.
-
变化度量: 为了比较改变配置后算法的相对排名变化情况, 假设在两个配置 \(c_1, c_2\) 下, 上述算法的排名根据某个推荐指标得到排名分别为 \(R_k^{(c_1)}, R_k^{(c_2)}\), 作者引入了两个指标来衡量两个排名的一致性:
- Overlap Ratio at top-\(k\) positions (\(OR@k\)):\[OR@k(c_1, c_2) = \frac{ |R_k^{(c_1)} \cap R_k^{(c_2)}| }{ k }, \]可以看到, \(OR@k\) 近关注排名前 top-\(k\) 的结果. 越大表示两个配置下 top-\(k\) 算法越一致.
- Spearman Rank Correlation (SRC):\[SRC (c_1, c_2) = 1 - \frac{ 6 \sum_{a \in \mathcal{A}} (r_a^{(c_1)} - r_a^{(c_2)})^2 }{ |\mathcal{A}|^3 - |\mathcal{A}| }, \]这里 \(\mathcal{A}\) 表示所有的算法, \(r_a\) 表示算法 \(a\) 的排名. 可以看到, \(SRC\) 是一个综合所有排名的指标. 越大表示两个配置下所有算法越一致.
- Overlap Ratio at top-\(k\) positions (\(OR@k\)):
Evaluation Metrics
- 首先, 作者调研不同的评价指标下, 对算法排名的影响, 主要考虑了如下的指标: Precision, Recall, F1, Mean Average Precision (MAP), Mean Reciprocal Rank (MRR), Normalized Discounted Cumulative Gain (NDCG), AUC, Novelty, Coverage.
Metric 的一致性
不同的 metrics 导致的算法排名差异
-
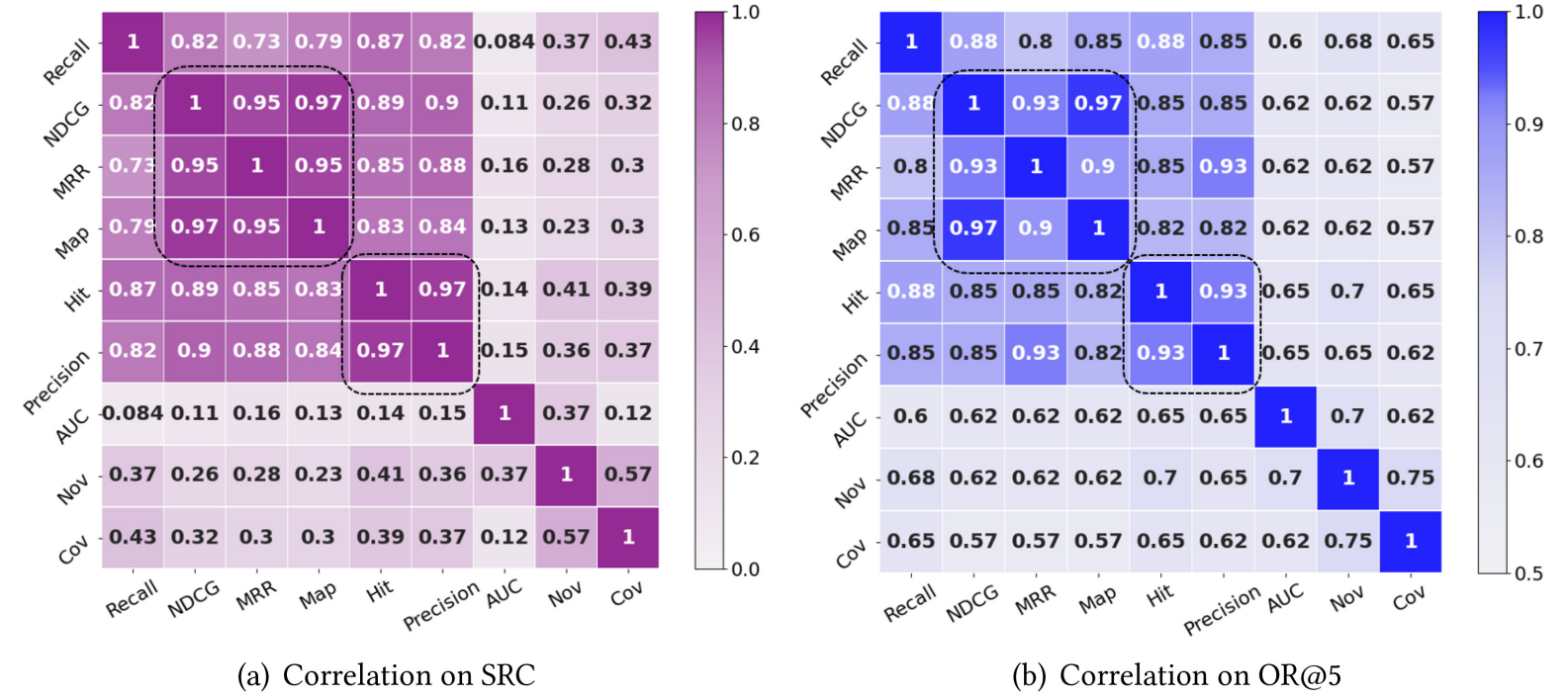
如上图所示, 虽然在不同指标下, 算法的排名不尽相同, 但总体可以分成如下的几组:
- Recall;
- NDCG, MRR, MAP;
- Hit, Precision;
- AUC;
- Novelty;
- Coverage.
-
总体上来说也是比较好理解, 每个 group 的指标在性质上本身就存在差异. 尤其是排序指标 NDCG, MAP 这种和多样性指标 Novelty, Coverage 之间.
-
不过比较有意思的是, 对于 top-\(k\) 算法而言, 也就是'最好'的那部分算法而言, 整体的一致性都比较好.
-
建议: 在评价一个算法的时候, 尽量挑选不同 group 中的指标.
Sampled metrics
- 虽然 sampled metrics 效率更高, 但是已经有论文指出 sampled metrics 的评估方式是有偏差的, 所以这篇文章进一步探究这个问题.
Sampled metrics 是否会导致和 full ranking 的 metrics 不同的评价
-
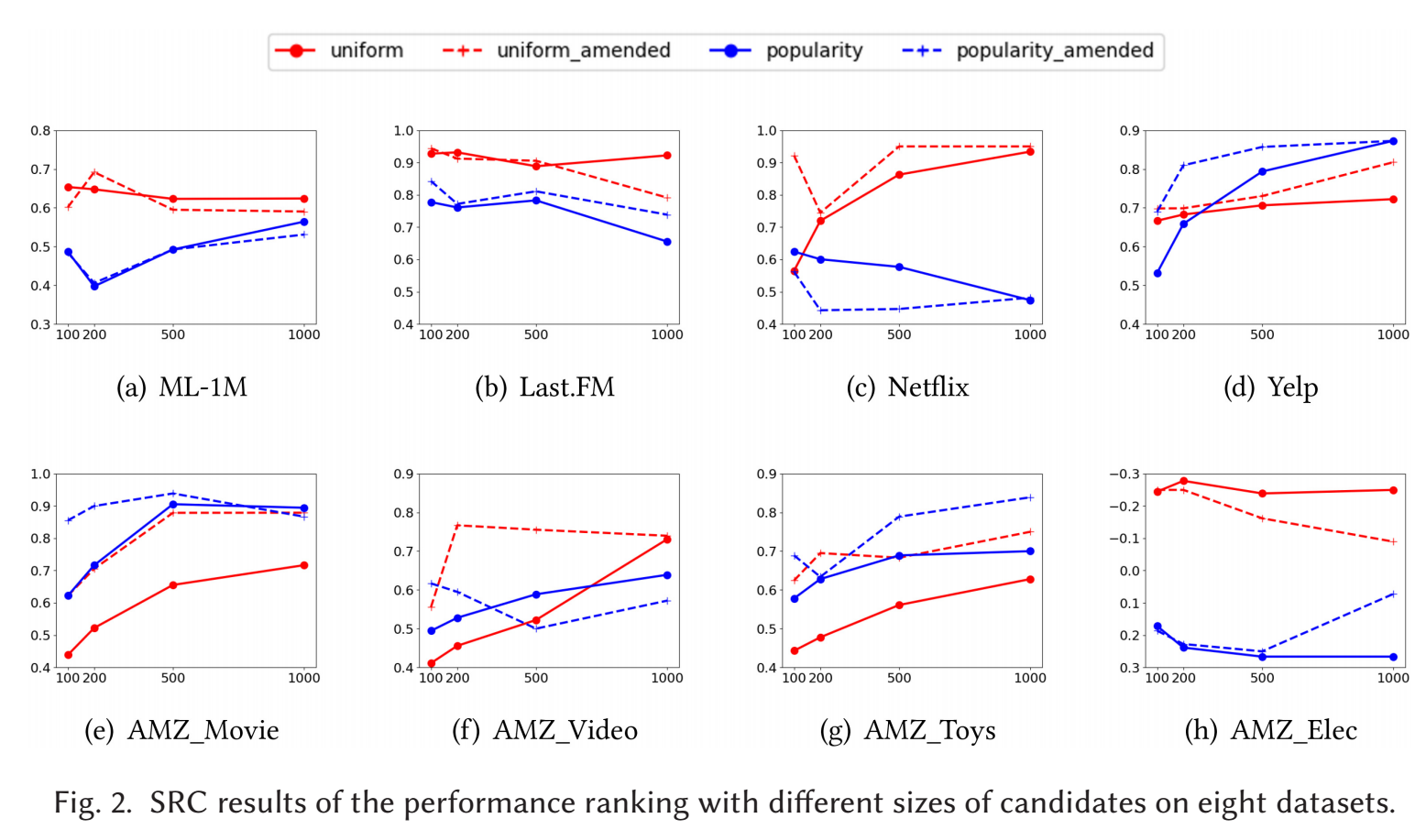
如上图所示, 横坐标是采样的负样本数量, 采样的方式有两种: 均匀采样和依照流行度采样. 可以发现:
- Uniform sampling 往往显示更好的效果, 且随着负样本数的增加越发趋近全量的评估;
- amendment 表示修正过 bias 的 sampled metrics, 但是作者发现其实效果并不明显.
-
进一步观测下方的 OR 的结果, 可以发现, 对于 top-\(k\) 的算法而言, 采取 sampled 或者全量的方式评估影响不大.
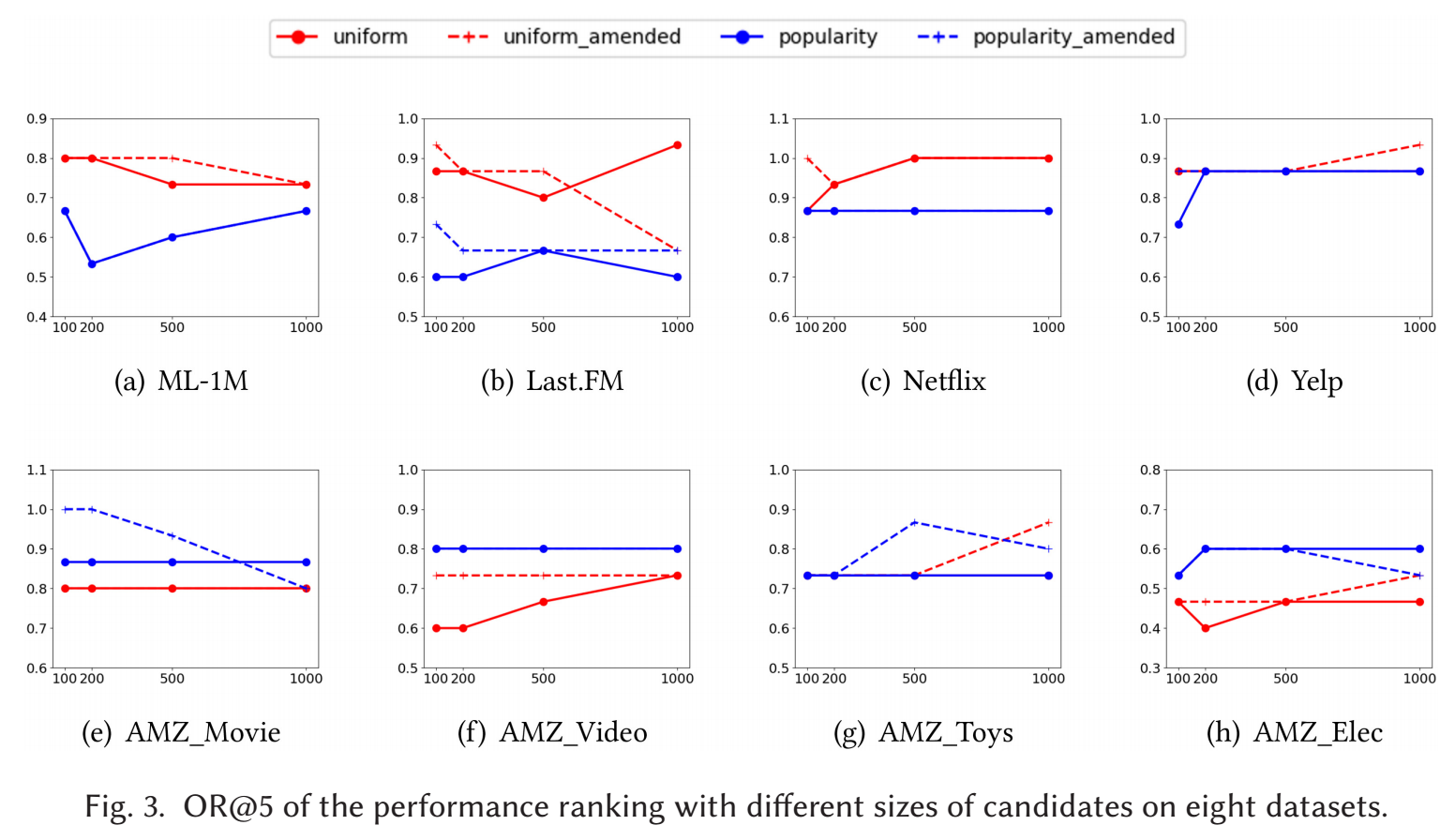
数据集构建
数据集的选择和预处理
\(k\)-core filtering 的影响
- 通常, 推荐数据集会进行这样的一个预处理, 即不断删除不活跃的 user/item 直到至少有 \(k\) 个 items/users. 那么这种预处理的方式影响有多大呢?
-
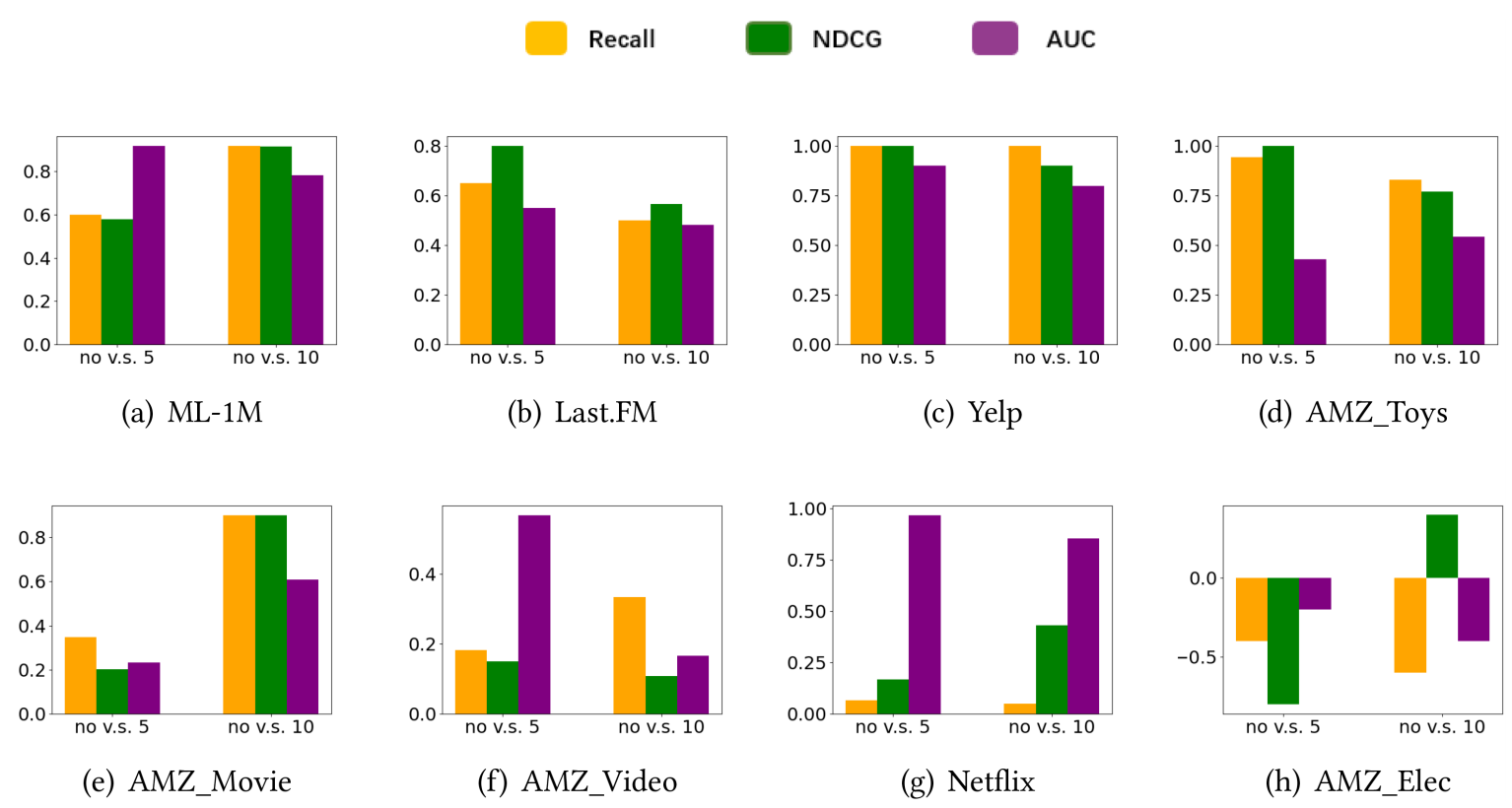
如上图所示, 并没有一致性的答案, 前后的差异和数据集有关系, 作者进一步猜测, 差异性程度和数据集 user, item 的各自交互比例有关系, 越平衡一致性越好.
-
建议: 数据集的选择应当覆盖 domian, sparsity, data characteristics.
数据集的切分
- 作者考虑了如下的四种切分方式:
- Rankdom Ordering Ratio-based Splitting (RO_RS): 随机打乱用户的交互, 然后用户的数据按照比例进行切分;
- Rankdom Ordering Leave-one-out Splitting (RO_LS): 随机打乱用户的交互, 然后用户的序列中的倒一和倒二分别作为测试和验证;
- Temporal Ordering Ratio-based Splitting (TO_RS): 按时间排列用户的交互, 然后用户的序列按照比例进行切分;
- Temporal Ordering Leave-one-out Splitting (TO_LS): 按时间排列用户的交互, 然后用户的序列中的倒一和倒二分别作为测试和验证.
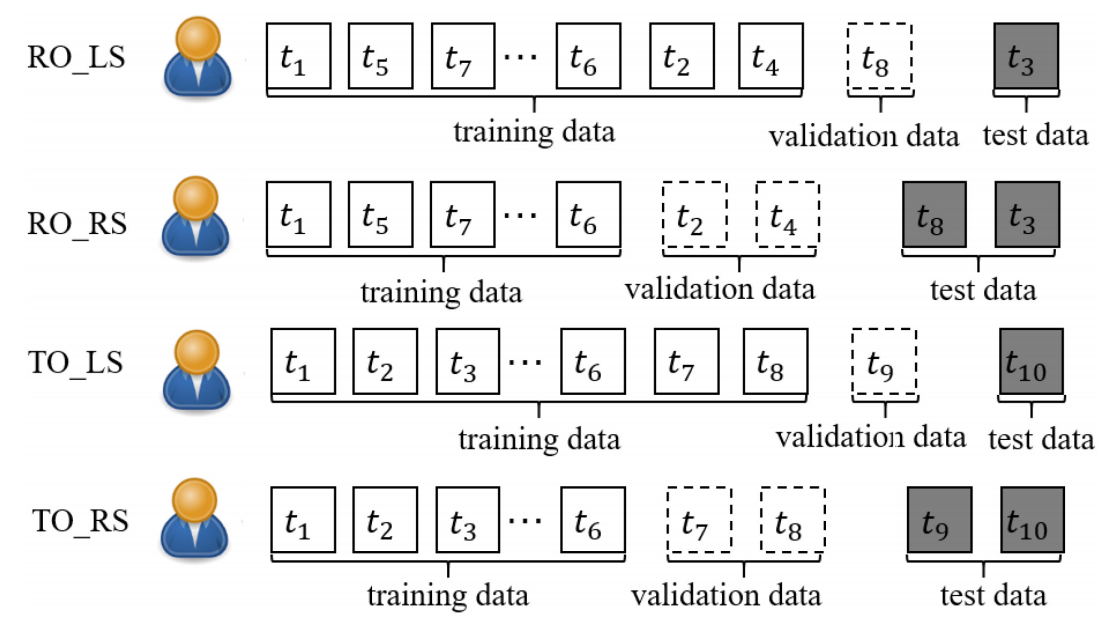
数据集的切分方式对结果的影响
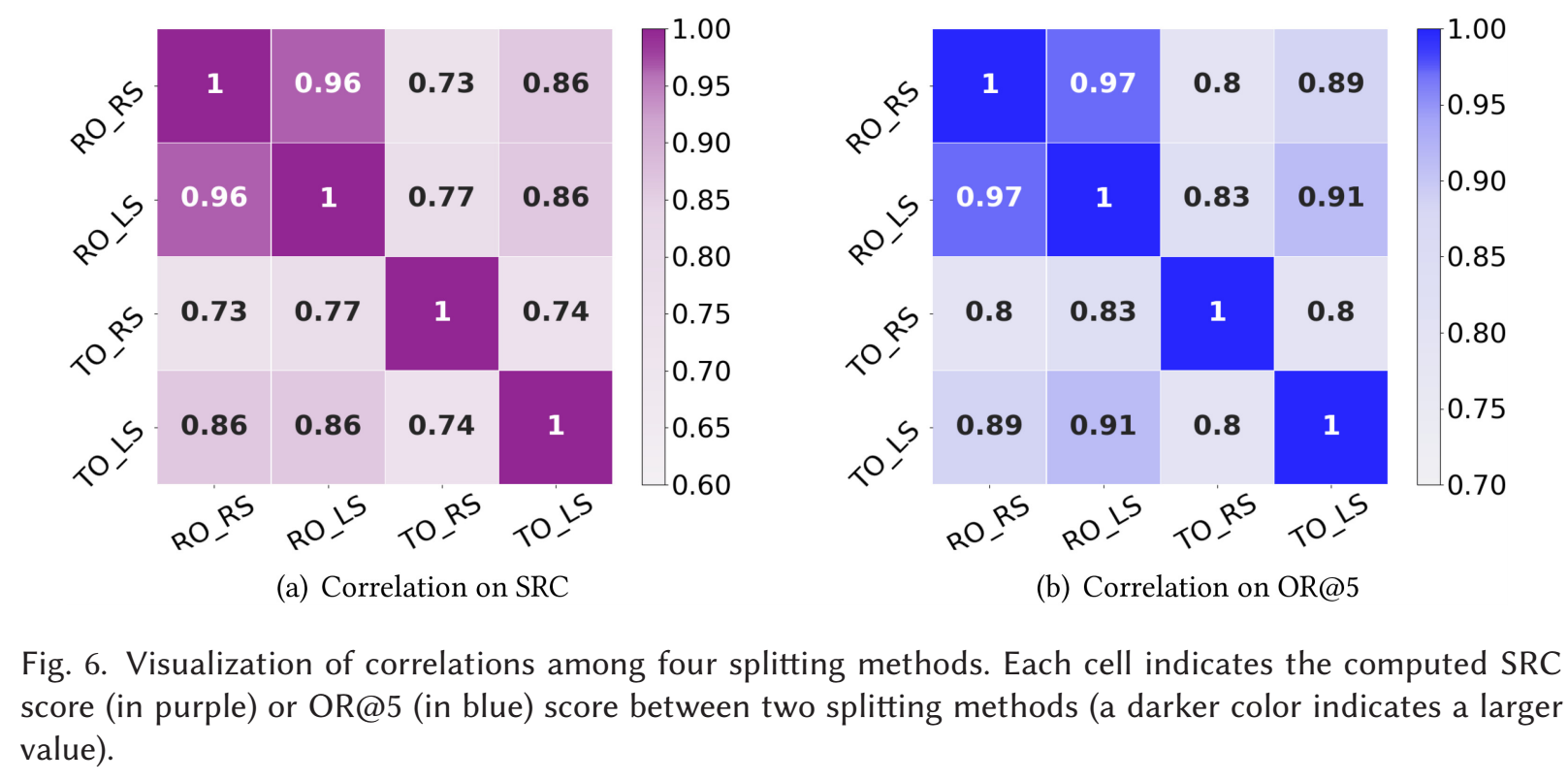
- Data set ordering 对结果的影响更为显著, 所以如果算法是时间相关的, 最好还是选择 temporal ordering 的方式.
数据集的切分方式对产生 invalid recommendations 的影响
-
上面讨论的方式, 实际上都可能会发生训练集测试集的时间线有重合的情况, 自然有可能会发生 invalid recommendations.
-
作者通过下列的方式来统计出现 invalid recommendations 的比例:
\[\#invalid = \frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \sum_{i \in \hat{R}_u} I( T_i^f \ge T_u^l ). \]其中 \(\hat{R}_u\) 表示给 \(u\) 的推荐列表, \(T_u^l\) 表示用户的最后的交互时间, \(T_i^f\) 表示 \(i\) 的第一次的出现时间.
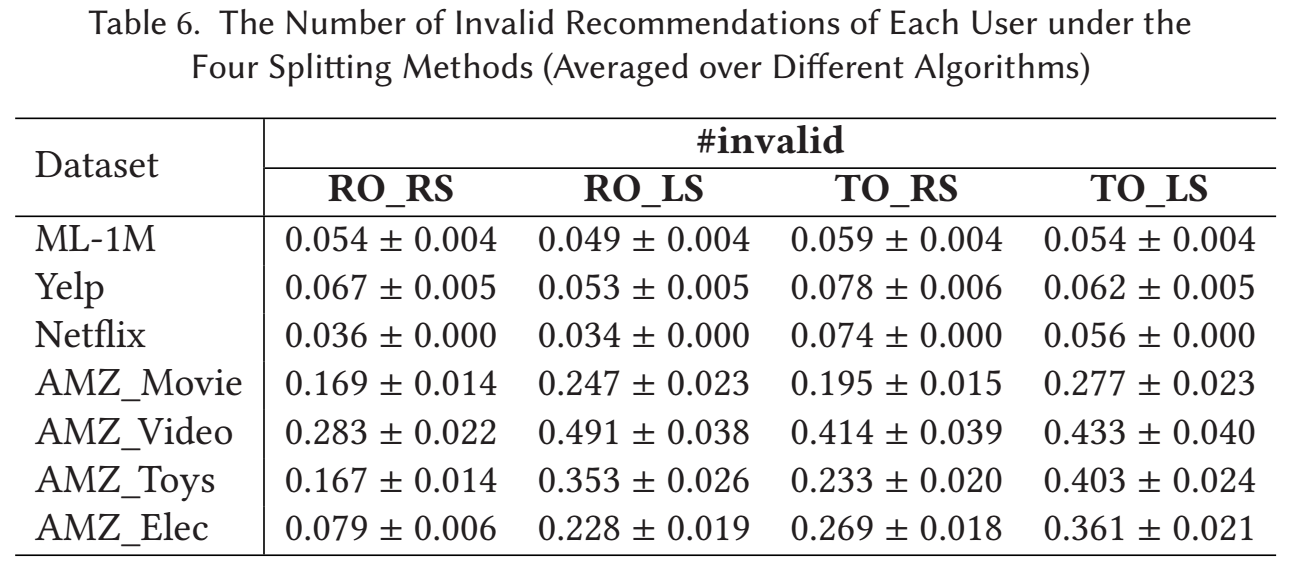
- 如上表所示, 总体来说 Temporal ordering 的方式会比 Rankdom ordering 的方式更容易产生更多的 invalid recommendations. 作者给了一点解释, 但是我感觉没啥道理.
模型优化
这块启发不是很大, 感兴趣的请回看原文.
代码
[official]
