BSL: Understanding and Improving Softmax Loss for Recommendation
概
作者'发现'在协同过滤中, Softmax loss 会比 BCE/BPR 损失效果好很多, 作者认为这是因为 Softmax 实际上等价于 Distributionally Robust Optimization, 所以能够对负样本中的一些噪声免疫, 故而如此有效. 作者进一步对其进行了改进, 使得它对正样本中的噪声也有一定的免疫.
符号说明
- \(\mathcal{U}\), users;
- \(\mathcal{I}\), items;
- \(\mathbf{R} \in \{0, 1\}^{|\mathcal{U}| \times |\mathcal{I}|}\), interaction matrix;
- \(\mathcal{S}_u^+ = \{i \in \mathcal{I}| r_{ui} = 1\}\), \(\mathcal{S}_u^- = \{i \in \mathcal{I}| r_{ui} = 0\}\);
Softmax loss
-
Softmax loss 定义为 (分子部分作者只保留了负样本):
\[\mathcal{L}_{SL}(u) = - \mathbb{E}_{i \in P_u^+} \bigg[ \log \frac{ \exp(f(u, i) / \tau) }{ N^- \mathbb{E}_{j \sim P_u^-}[ \exp(f(u, j) / \tau)] } \bigg]. \] -
作者认为上式可以归结为:
\[\mathcal{L}_{SL}(u) = \underbrace{-\mathbb{E}_{i \sim P_u^+}[f(u, i)]}_{\text{Positive Part}} + \underbrace{\tau \log \mathbb{E}_{j \sim P_u^-} [\exp( f(u, j) / \tau)]}_{\text{Negative Part}}, \]说实话, \(N^-\) 去掉式 ok 的毕竟是常数, 我不是很能理解 Negative Part 前的 \(\tau\) 是哪里来的.
-
DRO (Distributionally Robust Optimization) 是一种鲁棒优化的技术, 它形如:
\[ \hat{\theta} = \text{argmin}_{\theta} \{ \max_{P \in \mathbb{P}} \mathbb{E}_{x \sim P} [\mathcal{L}(x; \theta)] \}, \\ \mathbb{P} = \{P \in \mathbb{D}: D(P, P_o) \le \eta\}, \]即 DRO 认为, 最好的参数是使得在原始分布 \(P_o\) 周围的一些分布 \(P \sim \mathbb{P}\) 中的最坏情况也变得能够接受的参数. 所以 DRO 会导致保守但鲁棒的模型, 因而能够免疫一定噪声.
-
有这样的一个理论: 优化 Softmax loss 等价于在原来的 point-wise loss 上进行 Distributionally Robust Optimization. 故而, Softmax loss 相较于一般的 Point-wise loss 的优势便在于此.
-
此外, 作者还证明了, 优化 Softmax loss 对于 fairness 也是有帮助的 (参见原文).
-
\(\tau\) 的作用: 这套理论的优势在于, 能够从鲁棒性的角度去理解 \(\tau\). 根据上面理论的证明 (请看原文), 当 \(\tau\) 减小的时候, Softmax loss 的鲁棒性半径 \(\eta\) 减小, 于是变得越发极端, 反之变得越发保守:
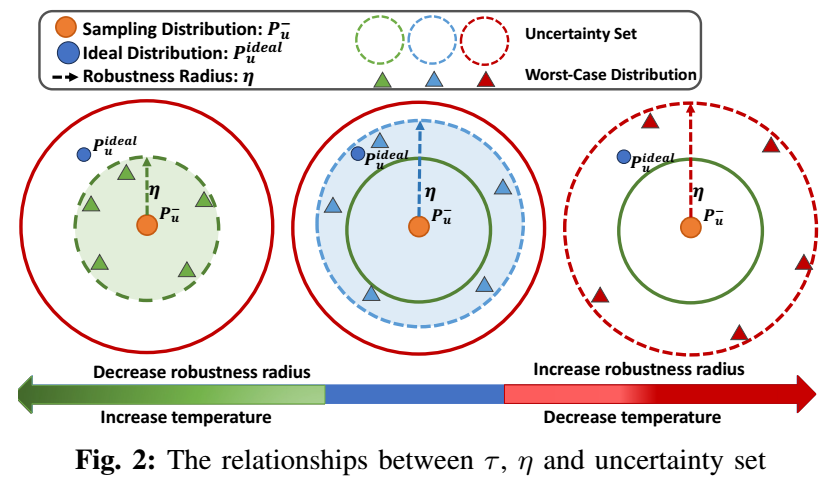
- 总而言之: 当你认为负样本的噪声很大的时候, 应该增大 \(\tau\), 反之减小 \(\tau\).
Bilateral Softmax loss (BSL)
- 作者进一步提出 BSL:\[\mathcal{L}_{BSL}(u) = \underbrace{-\tau_1 \log \mathbb{E}_{i \sim P_u^+} [\exp (f(u, i) / \tau_1)]}_{\text{Positive Part}} + \underbrace{\tau_2 \log \mathbb{E}_{j \sim P_u^-}[ \exp(f(u, j) / \tau_2) ]}_{\text{Negative Part}}. \]如此一来, 我们就可以通过 \(\tau_1\) 的调节来应对正样本中的噪声.
注: 如果每个用户采样的正样本数为 \(1\), 那 positive part 不久退化为了 \(f(u, i)\), 这样 \(\tau_1\) 不就没用了, 作者源代码里给的文章里说明好像有很大出入啊.
代码
- 作者提供了 Negative Sampling 和 In-Batch 两种方式的伪代码:
[official]
