DualGNN: Dual Graph Neural Network for Multimedia Recommendation

目录

• 概
• 符号说明
• DualGCN
• 代码

Wang Q., Wei Y., Yin J., Wu J., Song X. and Nie L. DualGNN: Dual graph neural network for multimedia recommendation. IEEE Transactions on Multimedia, 2023.

概

多模态 + user co-occureence graph -> recommendation.

文章中提到的 modality-missing 问题挺好的, 但是我并没有看到有什么特别的设计是解决这个问题的.

符号说明

• \(\mathcal{U}\), users, \(|\mathcal{U}| = N\);
• \(\mathcal{I}\), micor-videos, \(|\mathcal{I}| = M\);
• \(\mathcal{G} = (\mathcal{V}, \mathcal{E})\), interaction graph, \(\mathcal{V} = \mathcal{U} \cup \mathcal{I}\);
• \(m \in \mathcal{M} = \{v, a, t\}\), modality, \(v\): visual, \(a\): acoustic, \(t\): textual;
• \(\bm{u}_m^{(0)}\), 随机初始化的 user embedding for modality \(m\);
• \(\bm{i}_m^{(0)}\), modality features.

DualGCN

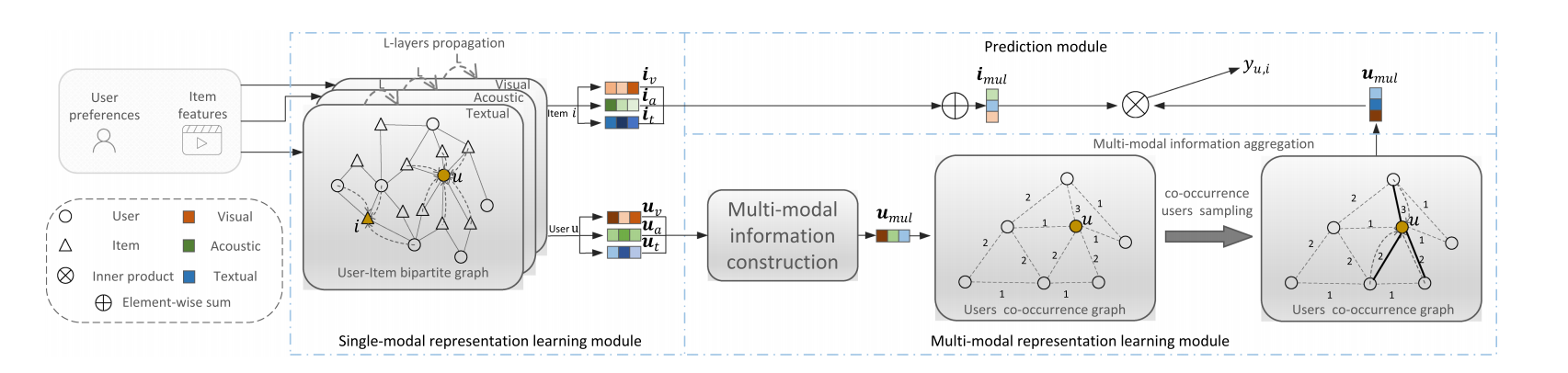
• 首先, 通过 user-item interaction graph, 对 user/item 的信息进行初步的转换, 这部分对于每个模态是独立的:

  \[\bm{u}_m^{(l+1)} = \sum_{i \in \mathcal{N}_u} \frac{ 1 }{ \sqrt{|\mathcal{N}_u|} \sqrt{|\mathcal{N}_i|} }\bm{i}_m^{(l)}, \\ \bm{i}_m^{(l+1)} = \sum_{i \in \mathcal{N}_u} \frac{ 1 }{ \sqrt{|\mathcal{N}_u|} \sqrt{|\mathcal{N}_i|} }\bm{i}_m^{(l)}, \]

  然后, 对各层求和:

  \[\bm{u}_m = \sum_{l=0}^L \bm{u}_m^{(l)}, \quad \bm{i}_m = \sum_{l=0}^L \bm{i}_m^{(l)}. \]

• 然后是, 多模态信息的一个融合, 用于得到用户的一个表征, 作者给了三种方案:

  1. Attentively concatenation construction:
     \[\bm{u}_{mul} = \bm{W}_m \bm{h}_u + \bm{b}_m, \\ \bm{h}_u = \alpha_{u, v} \bm{u}_v \| \alpha_{u, a} \bm{u}_a \| \alpha_{u, t} \bm{u}_t. \]

  2. Attentively sum construction:
     \[\bm{u}_{mul} = \alpha_{u,v} \bm{u}_v + \alpha_{u, a} \bm{u}_a + \alpha_{u, t} \bm{u}_t. \]

  3. Attentively maximum construction:
     \[\bm{u}_{mul} = \max( \alpha_{u, v} \bm{u}_v, \alpha_{u,a} \bm{u}_a, \alpha_{u, t} \bm{u}_t ). \]

• 接着 \(\bm{u}_{mul}\) 还要通过 user-user graph 来进行进一步的转换. 构造 co-occurrence graph, 对于每个 user, 作者取它的 top-K 个 frequent users 作为邻居, 便的权重赋为 \(1\), 其它为 0. 接下来通过下列二者之一的方式进行转换:

  1. Mean aggregation:
     \[\bm{u}_{mul}^{(l'+1)} = \bm{u}_{mul}^{(l')} + \sum_{u' \in \mathcal{N}_{u, c}} \frac{1}{|\mathcal{N}_{u, c}|} {\bm{u}_{mul}'}^{(l')}, \]
     其中 \(\mathcal{N}_{u,c}\) 表示 user \(u\) 的 top-\(K\) 邻居.
  2. Softmax weighted aggregation:
     \[\bm{u}_{mul}^{(l'+1)} = \bm{u}_{mul}^{(l')} + \sum_{u' \in \mathcal{N}_{u, c}} \frac{ \exp(C_{u, u'}) }{ \sum_{u' \in \mathcal{N}_{u, c}} \exp(C_{u, u'}) } {\bm{u}_{mul}'}^{(l')}, \]
     其中 \(C_{u, u'}\) 表示 users \(u, u'\) 的 co-occurrence times.

• 最后得到最终 user/item 的表示:

  \[\bm{u}^* = \bm{u}_{mul}^{(L')}, \quad \bm{i}^* = \bm{i}_v + \bm{i}_a + \bm{i}_t. \]

  然后 score 的预测通过内积得到

  \[y_{u,i} = {\bm{u}^*}^T \bm{i}^*. \]

• 训练通过 BPR 损失.

代码

[official]