A Tale of Two Graphs: Freezing and Denoising Graph Structures for Multimodal Recommendation

目录

• 概
• FREEDOM
  • Motivation
  • Frozen Item-Item graph
  • Denoising User-Item Bipartite Graph
  • Two Graphs for Learning
• 代码

Zhou X. and Shen Z. A tale of two graphs: Freezing and denoising graph structures for multimodal recommendation.

概

本文主要是对 LATTICE 的改进.

FREEDOM

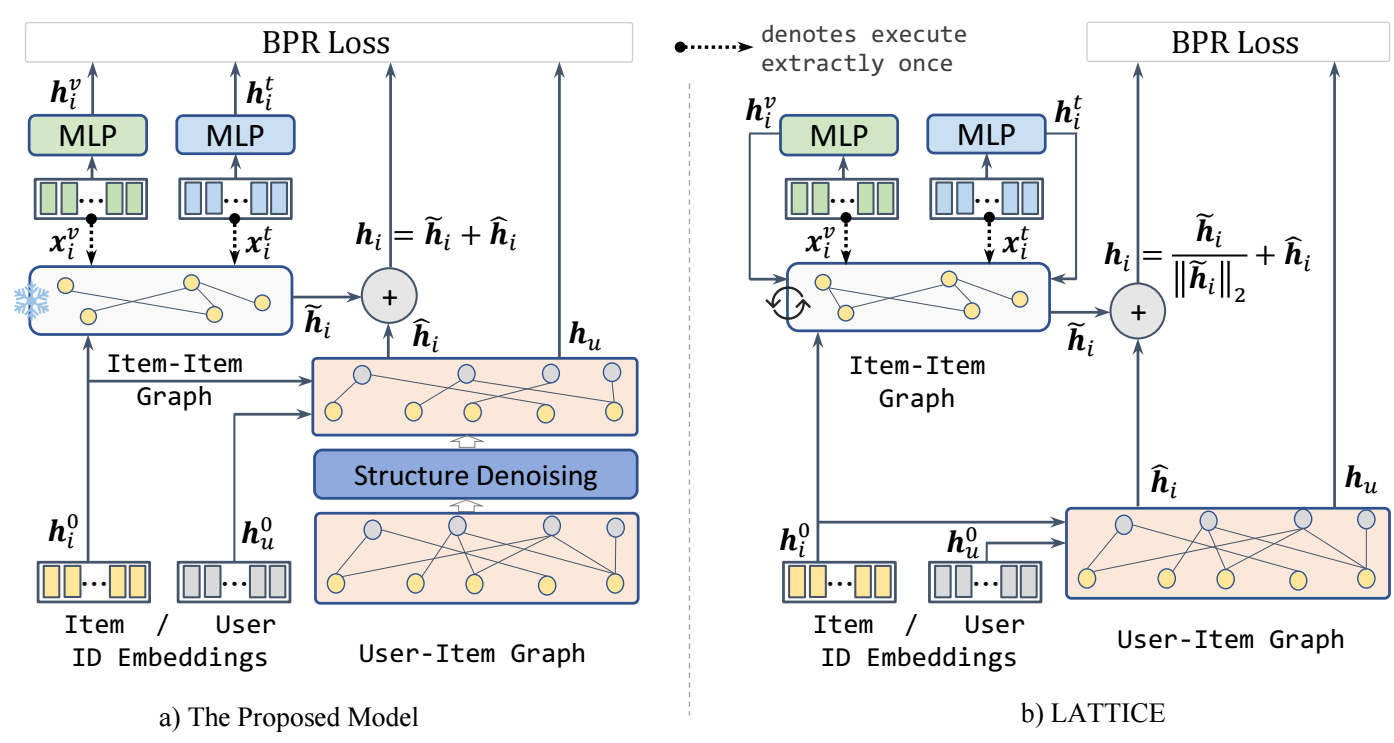
Motivation

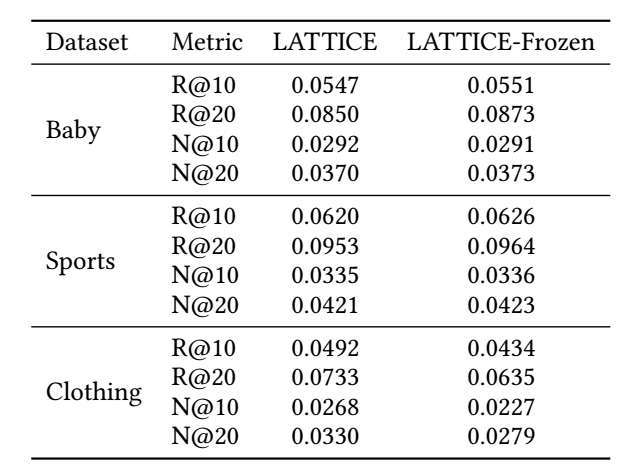
• 如上图所示, LATTICE 动态地抽取 modality-specific 的 graph, 但是作者发现, 固定下来反而会有更好的结果:
  

Frozen Item-Item graph

• 假设每个模态 $m \in \mathcal{M}$ 的节点特征为 $\bm{x}_i^m$, 通过如下方式初步估计两两间的关系:

  $$S_{ij}^m = [\frac{ (\bm{x}_i^m)^T \bm{x}_j^m }{ \|\bm{x}_i^m\| \|\bm{x}_j^m\| }]_+,$$

  其中 $[\cdot]_+ = \max(\cdot, +)$,
  接着, 每个 item, 我们取相似度最高的 top-$k$ 个作为实际的邻居:

  $$\hat{S}_{ij}^m = \left \{ \begin{array}{ll} S_{ij}^m, & S_{ij}^m \in \text{top-}k (S_i^m), \\ 0, & \text{otherwise}. \end{array} \right .$$

  最后我们再对这个稀疏化后的邻接矩阵进行标准化:

  $$\tilde{S}^m = (D^m)^{-1/2} \hat{S}^m (D^m)^{-1/2}.$$

  其中 $D^m$ 为 $\hat{S}^m$ 的度矩阵.

• 最后, 通过如下方式聚合多个模态的邻接矩阵:

  $$S = \sum_{m \in \mathcal{M}} \alpha_m \tilde{S}^m.$$

  对于本文所考虑的仅 textual (t) + visual (v) 两个模态的信息, 作者设置为

  $$\alpha_v, \alpha_t = 1 - \alpha_v,$$

  然后 $\alpha_v$ 是一个认为给定的超参数 (LATTICE 中是可训练的参数, 所以从这个点来说, FREEDOM 似乎不那么直接地推广到更多地模态).

Denoising User-Item Bipartite Graph

• 其它部分, FREEDOM 和 LATTICE 差别不大, 另一个比较明显差别是对于 User-Item graph 的处理, 简而言之, FREEDOM 的 user-item 图是"动态"采样的.

• 假设 User-Item 的交互图为 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$, 每条边的权重的采样概率为

  $$p_{e_{ij}} = \frac{1}{ \sqrt{\omega_i} \sqrt{\omega_j} }, \quad e_{ij} \in \mathcal{E}.$$

  其中 $\omega_i$ 表示节点 $i$ 的度数. 故而, 一条边若是连接了高度数的节点, 则它有比较小的概率被采样到.

• 我们用 $\hat{A}_{\rho}$ 来表示采样后且标准化后的图.

Two Graphs for Learning

• 接下来, 用上面得到的两个图进行特征的提取.

• 对于模态的图, 我们用于处理 item 的 embedding:

  $$\tilde{\bm{h}}_i^l = \sum_{j \in \mathcal{N}(i)} S_{ij} \tilde{\bm{h}}_j^{l-1}, \quad \bm{h}_i^0 = \bm{x}_i.$$

• 接着, 对于 user-item graph, 作者利用 LightGCN 得到

  $$\hat{\bm{h}}_u, \hat{\bm{h}}_i.$$

• 最后我们将两部分的 embeddiing 融合在一起得到:

  $$\bm{h}_u = \hat{\bm{h}}_u, \\ \bm{h}_i = \tilde{\bm{h}}_i + \hat{\bm{h}}_i.$$

  除此之外, 还有 modality-specific 的特征

  $$\bm{h}_i^m = \bm{x}^m W_m + \bm{b}_m.$$

• 最后通过如下的损失进行训练:

  $$\mathcal{L}_{bpr} = \sum_{(u, i, j) \in \mathcal{D}} \bigg( -\log \sigma(\bm{h}_u^T \bm{h}_i - \bm{h}_u^T \bm{h}_j) + \lambda \sum_{m \in \mathcal{M}} -\log \sigma ( \bm{h}_u^T \bm{h}_i^m - \bm{h}_u^T \bm{h}_j^m ) \bigg).$$

代码

[official]