KGAT Knowledge Graph Attention Network for Recommendation
概
知识图谱 for 推荐系统.
符号说明
-
\(\mathcal{G}_1 = \{(u, y_{ui}, i)| u \in \mathcal{U}, i \in \mathcal{I}\}\), \(y_{ui} = 1\) 表示 \(u\) 曾经交互过 \(i\), \(y_{ui} = 0\) 则代表 \(u\) 未曾交互过 \(i\);
-
\(\mathcal{G}_2 = \{(h, r, t)| h, t \in \mathcal{E}, r \in \mathcal{R}\}\), knowledge graph, \(\mathcal{E}\) 表示 knowledge graph 中的 entities, \(\mathcal{R}\) 表示各种关系;
-
\(\mathcal{G} = \{(h, r, t)| h, t \in \mathcal{E}', r \in \mathcal{R}'\}\), collaborative knowledge graph, \(\mathcal{E}' = \mathcal{E} \cup \mathcal{U}\), \(\mathcal{R}' = \mathcal{R} \cup \{\text{Interact}\}\).
KGAT
KGAT 分为两个步骤, 一个是普通的知识图谱的 embedding 建模, 另外一个是协同过滤的任务.
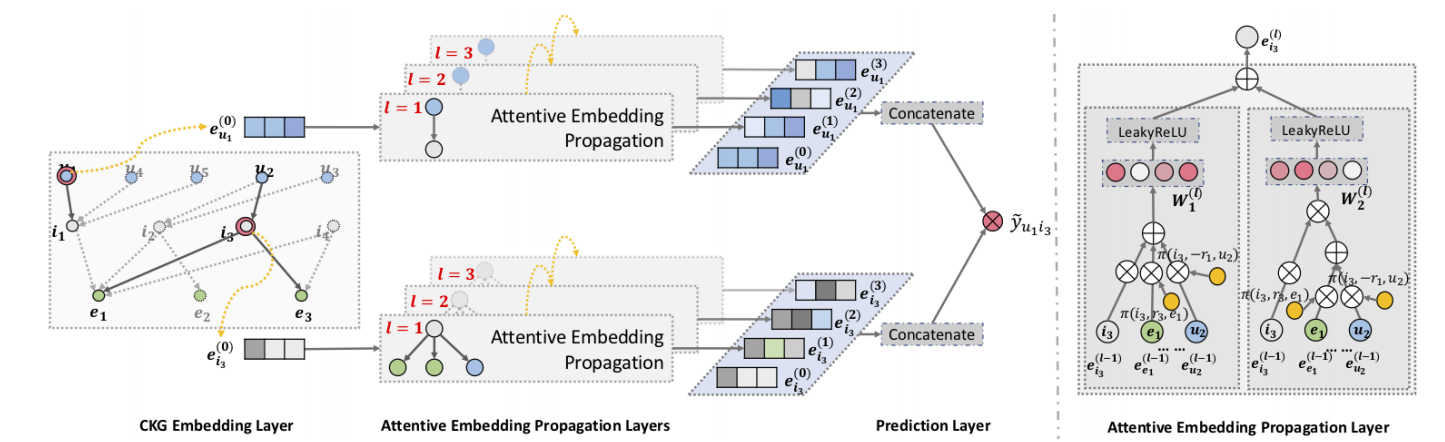
Embedding Layer
-
对于知识图谱的 embedding 建模, 作者遵循的是 TransR 的方法, 对于关系三元组 \((h, r, t)\), 对应的 embedding 为 \((\mathbf{e}_h, \mathbf{e}_r, \mathbf{e}_t) \in \mathbb{R}^{d \times d}\), TransR 度量三元组的关系
\[g(h, r, t) = \|\mathbf{W}_r \mathbf{e}_h + \mathbf{e}_r - \mathbf{W}_r \mathbf{e}_t \|_2^2, \]这里 \(\mathbf{W}_r \in \mathbb{R}^{k \times d}\) 是将 \(\mathbf{e}_h, \mathbf{e}_r\) 映射到和 \(\mathbf{e}_r\) 一样的隐空间中.
-
然后通过如下损失进行训练
\[\mathcal{L}_{\text{KG}} =\sum_{(h, r, t, t') \in \mathcal{T}} -\ln \sigma \bigg( g(h, r, t') - g(h, r, t) \bigg). \]其中 \((h, r, t)\) 表示真实存在的三元组, \((h, r, t')\) 则是负样本.
Attentive Embedding Propagation Layers
-
接下来, KGAT 通过图网络进行信息传播, 对于 entity \(h\), 它和它周围的邻居按照如下方式进行更新:
\[ \mathbf{e}_{\mathcal{N}_h} = \sum_{(h, r, t) \in \mathcal{N}_h} \pi (h, r, t) \mathbf{e}_t, \]其中 \(\pi(h, r, t)\) 为 knowledge-aware attention, 按照如下方式计算:
\[ \pi(h, r, t) = \frac{ \exp( \pi(h, r, t)) }{ \sum_{(h, r', t') \in \mathcal{N}_h} \exp(\pi(h, r', t')) }, \\ \hat{\pi}(h, r, t) = (\mathbf{W}_r \mathbf{e}_t)^T \tanh \big( (\mathbf{W}_r \mathbf{e}_h + \mathbf{e}_r) \big). \] -
然后按照如下三种方式之一进行节点更新:
- GCN:\[ f_{\text{GCN}} = \text{LeakyReLU}\big( \mathbf{W}(\mathbf{e}_h + \mathbf{e}_{\mathcal{N}_h}) \big); \]
- GraphSage:\[ f_{\text{GraphSage}} = \text{LeakyReLU}\big( \mathbf{W}(\mathbf{e}_h \| \mathbf{e}_{\mathcal{N}_h}) \big); \]
- Bi-Interaction:\[ f_{\text{Bi-Interaction}} = \text{LeakyReLU}\big( \mathbf{W}_1(\mathbf{e}_h + \mathbf{e}_{\mathcal{N}_h}) \big) + \text{LeakyReLU}\big( \mathbf{W}_1(\mathbf{e}_h \odot \mathbf{e}_{\mathcal{N}_h}) \big). \]
- GCN:
-
按照类似的方式, 不断迭代更新, 得到多层的节点表示:
\[ \{ \mathbf{e}_u^{(1)}, \cdots, \mathbf{e}_u^{(L)} \}. \] -
最后 user/item 的节点表示为:
\[\mathbf{e}_u^* = \mathbf{e}_u^{(0)} \| \cdots \| \mathbf{e}_u^{(L)}, \quad \mathbf{e}_i^* = \mathbf{e}_i^{(0)} \| \cdots \| \mathbf{e}_i^{(L)}. \] -
然后评分预测为:
\[ \hat{y}(u, i) = {\mathbf{e}_u^*}^T \mathbf{e}_i^*. \] -
协同过滤的损失为:
\[ \mathcal{L}_{\text{CF}} = \sum_{(u, i, j) \in \mathcal{O}} -\ln \sigma \big( \hat{y}(u, i) - \hat{y}(u, j) \big). \] -
最终的损失为:
\[ \mathcal{L}_{\text{KGAT}} = \mathcal{L}_{\text{KG}} + \mathcal{L}_{\text{CF}} + \lambda \|\Theta\|_2^2. \]
代码
[official]


