TransE, TransH, TransR
概
-
\(G = \{(h, r, t)\}\), 每个三元组 \((h, r, t)\) 代表 \(h \mathop{\longrightarrow} \limits^{r} t\).
-
\(\bm{h}, \bm{r}, \bm{t}\), 分别表示头实体 \(h\), 关系 \(r\), 和 尾实体 \(t\) 的 embedding.
TransE|H|R
-
知识图谱的核心目标是预测两个实体间的关系. 具体的, 我们希望训练这样的一个打分函数 \(f\), 若 \((h, r, t)\) 是真实存在的关系, 则 \(f(h, r, t)\) 应该返回一个较高的值, 否则返回一个较低的值.
-
TransE 的做法就是用负距离来进行度量:
\[ f(h, r, t) := -d(h, r, t) = - \| \bm{h} + \bm{r} - \bm{t} \|_2^2. \] -
但是这种方式在一些情况下是存在问题的, 比如:
- 关系 \(r\) 是双向的, 即\[h \mathop{\longrightarrow} \limits^{r} t \Leftrightarrow t \mathop{\longrightarrow} \limits^{r} h, \]此时最理想的情况:\[\bm{h} + \bm{r} - \bm{t} = \bm{t} + \bm{r} - \bm{h} = \bm{0} \Rightarrow \bm{h} = \bm{t}, \bm{r} = \bm{0}. \]这显然不合理;
- 此外, 倘若存在多个头实体共同对应一个尾实体, 比如\[h_1, h_2 \mathop{\longrightarrow} \limits^{r} t, \]此时, 最理想的情况是:\[\bm{h}_1 + \bm{r} - \bm{t} = \bm{h}_2 + \bm{r} - \bm{t} = \bm{0} \Rightarrow \bm{h}_1 = \bm{h}_2. \]这实际上也不合理.
- 关系 \(r\) 是双向的, 即
-
于是 TransH 提出了一个改进, 它的度量方式改为:
\[d(h, r, t) = \| \bm{h}_{\perp} + \bm{r} - \bm{t}_{\perp}\|_2^2, \\ \bm{h}_{\perp} = \bm{h} - (\bm{w}_r^T \bm{h}) \bm{w}_r, \\ \bm{t}_{\perp} = \bm{t} - (\bm{w}_r^T \bm{t}) \bm{w}_r. \]其中 \(\|\bm{w}_r\|_2 = 1\). 故而 \(\bm{h}_{\perp}, \bm{t}_{\perp}\) 实际上是到 \(\bm{w}_r\) 上的垂线,
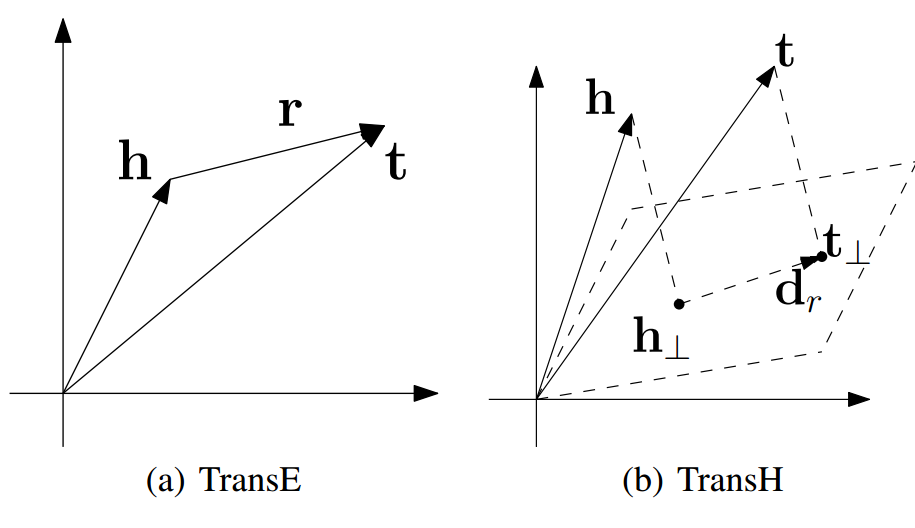
-
TransR 则是把 \(\bm{h}, \bm{t}\) 通过一个变换矩阵映射到关系 \(\bm{r}\) 所在的空间中:
\[d(h, r, t) = \| \bm{h}_r + \bm{r} - \bm{t}_r \|_2^2, \\ \bm{h}_r = \mathbf{W}_r \bm{h}, \quad \bm{t}_r = \mathbf{W}_r \bm{t}. \]且限制:
\[\|\bm{h}\|_2 \le 1, \|\bm{r}\|_2 \le 1, \|\bm{t}\|_2 \le 1, \|\bm{h}_r\|_2 \le 1, \|\bm{t}_r\|_2 \le 1. \] -
最后的损失为,
\[\mathcal{L} = \sum_{(h, r, t)} \sum_{(h', r, t')} \max (0, d(h, r, t) + \gamma - d(h', r, t')), \]其中 \((h', r, t')\) 表示 incorrect triples. \(\gamma\) 表示 margin.


