Towards Foundation Models for Knowledge Graph Reasoning
概
如何从不同领域的图中学习的有价值的可迁移的信息是通往 graph foundation model 的根本. 本文在多关系建模问题 (主要围绕知识图谱推理) 上给出了一个极为简单却有效的方案.
符号说明
- \(\mathcal{V}\), nodes;
- \(\mathcal{R}\), edge types;
- \(\mathcal{E}\), edges, \(e \in \mathcal{E}\) 表述为 triplet \((h, r, t)\).
- \(\mathcal{G} = (\mathcal{V}, \mathcal{R}, \mathcal{E})\), knowledge graph;
ULTRA (a method for Unified, Learnable, and TRAnsferable KG representations)
- 只是图谱的推理问题是回答如下的问题:\[ (h, r, ?): \text{何尾实体与头实体 h 存在关系 r}, \\ (?, r, t): \text{何头实体与尾实体 t 存在关系 r}. \\ \]
-
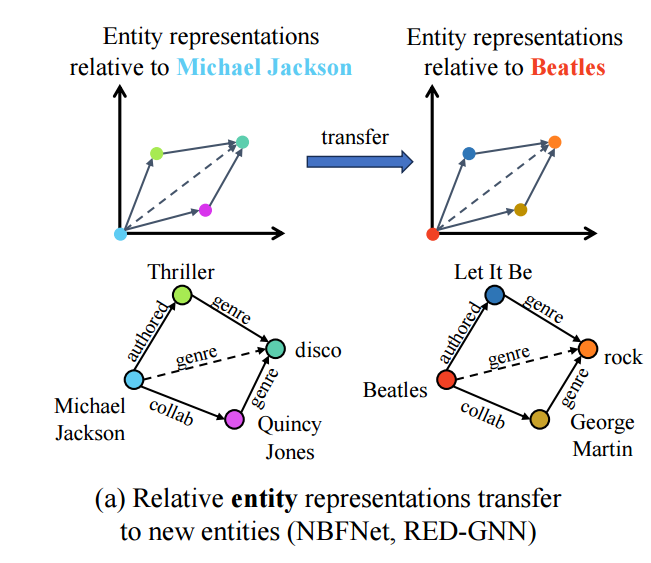
Transductive: 如上图所示, 我们可以得出一个比较直接的结论. 一步步地,
- Michael Jackson 创作了 (authored) Thriller, 属于 disco 流派 (genre);
- 他的合作者 Quincy Jones 属于 disco 流派;
- 则我们可以推断出 Michael Jackson 的流派也是 disco.
- 倘若模型学到了这种结构关系, 那么我们很容易也能得出:\[ \text{Beatles} \mathop{\longrightarrow} \limits^{authored} \text{Let It Be} \mathop{\longrightarrow} \limits^{genre} \text{rock} \wedge \text{Beatles} \mathop{\longrightarrow} \limits^{collab} \text{George Martin} \mathop{\longrightarrow} \limits^{genre} \text{rock} \]可以推断出: \(\text{Beatles} \mathop{\longrightarrow} \limits^{genre} \text{rock}\).
-
但是学到这种关系的模型往往无法直接运用到一些别的领域上, 经过关系的模式是非常相似的. 比如:
-
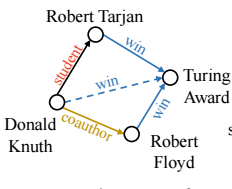
几乎是一样的推理规则, 但是由于这些 entities 或者 edge types 未曾见过, 导致模型无法直接应用.
-
本文提出的 ULTRA 来一般性的学习这些关系间的关系, 然后介绍如何推广到 inductive 的环境中.
Relation Graph Construction
- ULTRA 将知识图谱 \(\mathcal{G} = (\mathcal{V}, \mathcal{R}, \mathcal{E})\) 转换为新的图 \(\mathcal{G}_r = (\mathcal{V}', \mathcal{R}', \mathcal{E}')\):
- \(\mathcal{V}' = \mathcal{R}\);
- \(\mathcal{R}'\) 包括:
- tail-to-head (t2h): \((r_1, t2h, r_2)\) 说明 \(\mathcal{G}\) 中存在 \(a \mathop{\longrightarrow} \limits^{r_1} b \mathop{\longrightarrow} \limits^{r_2} c\);
- head-to-head (h2h): \((r_1, h2h, r_2)\) 说明 \(\mathcal{G}\) 中存在 \(a \mathop{\longleftarrow} \limits^{r_1} b \mathop{\longrightarrow} \limits^{r_2} c\);
- head-to-tail (h2t): \((r_1, h2t, r_2)\) 说明 \(\mathcal{G}\) 中存在 \(a \mathop{\longleftarrow} \limits^{r_1} b \mathop{\longleftarrow} \limits^{r_2} c\);
- tail-to-tail (t2t): \((r_1, t2t, r_2)\) 说明 \(\mathcal{G}\) 中存在 \(a \mathop{\longrightarrow} \limits^{r_1} b \mathop{\longleftarrow} \limits^{r_2} c\);
- \(\mathcal{E}'\) 的确定根据如上的关系.
-
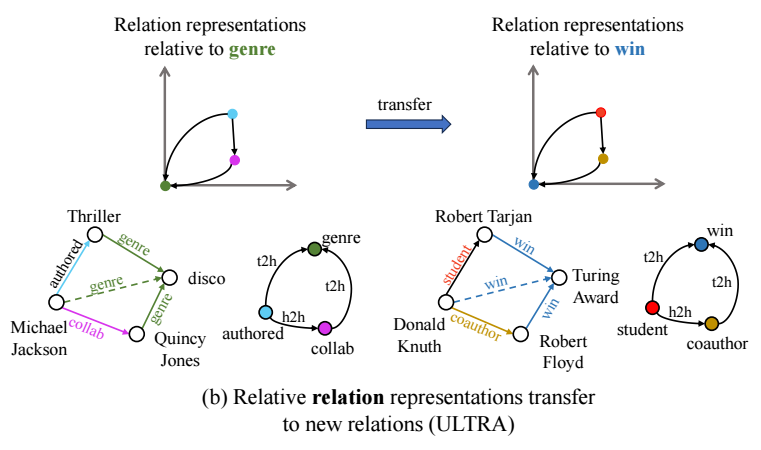
上图给了一个实际的例子.
-
大部分的基于 GNN 的推理都离不开邻接矩阵, 我们来说明如何得到 \(\mathcal{G}'\) 的邻接矩阵. 首先, 我们定义 \(\mathcal{G}\) 的邻接矩阵为 \(\bm{A} \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{R}| \times |\mathcal{V}|}\). 每一条边 \(e\), 实际上我们都可以拆成:
\[ (h, r), (r, t) \]于是, 我们可以构建得到:
\[ \bm{E}_h \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{R}|}, \bm{E}_t \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{R}|}, \]满足:
\[ [\bm{E}_h]_{ar} \not = 0, \quad \text{if } \exist (a, r, ?) \in \mathcal{E}, \\ [\bm{E}_t]_{br} \not = 0, \quad \text{if } \exist (?, r, b) \in \mathcal{E}. \] -
则
\[ \bm{A}_{h2h} = \text{spmm}(\bm{E}_h^T, \bm{E}_h) \in \mathbb{R}^{|\mathcal{R}| \times |\mathcal{R}|}, \\ \bm{A}_{t2t} = \text{spmm}(\bm{E}_t^T, \bm{E}_t) \in \mathbb{R}^{|\mathcal{R}| \times |\mathcal{R}|}, \\ \bm{A}_{h2t} = \text{spmm}(\bm{E}_h^T, \bm{E}_t) \in \mathbb{R}^{|\mathcal{R}| \times |\mathcal{R}|}, \\ \bm{A}_{t2h} = \text{spmm}(\bm{E}_t^T, \bm{E}_h) \in \mathbb{R}^{|\mathcal{R}| \times |\mathcal{R}|}, \\ \bm{A}_r = [\bm{A}_{h2h}, \bm{A}_{t2t}, \bm{A}_{h2t}, \bm{A}_{t2h}] \in \mathbb{R}^{|\mathcal{R}| \times |\mathcal{R}| \times 4}. \]
Conditional Relation Representations
-
现在, 我们来将怎么依靠 \(\mathcal{G}_r\) 训练和推理. 主要是依靠一些 inductive learning 方法, 本文基于 NBFNet:
\[\tag{1} \bm{h}_{v|u}^{0} = \mathbb{I}_{u=v} \odot \mathbf{1}^d, \\ \bm{h}_{v|u}^{t+1} = \text{Update} \bigg( \bm{h}_{v|u}^{t}, \text{Aggregate} \big( \text{Message}(\bm{h}_{w|u}^t, \bm{r}) | w \in \mathcal{N}_r(u), r \in \mathcal{R}' \big) \bigg). \]注意到, 上面的过程中不涉及特定的 node features, 而是仅为 node \(u\) 初始化为 \(\mathbf{1}^d\) 其余为 \(\bm{0}\), 故而可以推广到任意图. 其它的细节请看 NBFNet.
-
假设我们通过 (1) 在多个 relation graphs \(\mathcal{G}_r\) (涉及不同的领域) 训练好, 然后我们想要在一个新的图 \(\mathcal{G}\) 上进行推理怎么办?
- 将这个新的图 \(\mathcal{G}\) 转换为 relation graph, 然后用之前的模型在其上推理, 得到表示 \(\bm{R}_q \in \mathbb{R}^{|\mathcal{R}| \times d}\). 注意, 这个表示是 query \(q\) 依赖的.
- 作者额外再利用一个 NBFNet 进行 link prediction:\[ \bm{h}_{v|u}^{0} = \mathbb{I}_{u=v} \odot \bm{R}_q[q], \\ \bm{h}_{v|u}^{t+1} = \text{Update} \bigg( \bm{h}_{v|u}^t, \text{Aggregate} \big( \text{Message}( \bm{h}_{w|u}^t, g^{t+1} (\bm{r})) | w \in \mathcal{N}_r(v), r \in \mathcal{R}. \big) \bigg) \]
-
需要注意, 上面两个阶段所涉及的参数都可以在一些数据集上预训练, 然后直接应用在下游的一些任务上, 从而实现 zero-shot 的推理. 也可以在下游任务进行一些微调. 具体的训练方式, 作者采取 BCE 进行训练.
代码
[official]
