ROLAND Graph Learning Framework for Dynamic Graphs
You J., Du T. and Leskovec J. ROLAND: Graph learning framework for dynamic graphs. KDD, 2022.
概
dynamic graphs 中比较系统性的工作.
符号说明
- \(V = \{v_1, \ldots, v_n\}\), node set;
- \(E \subset V \times V\), edge multi-set;
- \(G = (V, E)\), graph;
- \(X = \{\mathbf{x}_v| v \in V\}\), node features;
- \(F = \{\mathbf{f}_{uv} | (u, v) \in E\}\), edge features
- \(\mathcal{G} = \{G_t\}_{t=1}^T\), dynamic graph: a sequence of graph snapshots;
Motivation
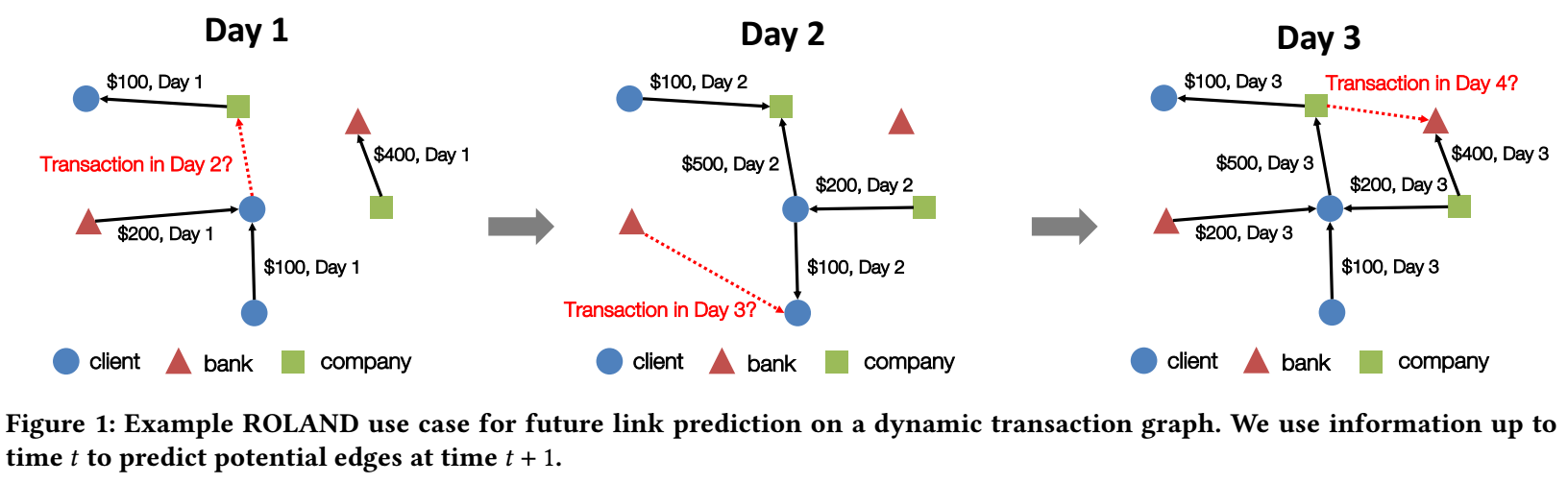
- 图神经网络在动态图上的研究还不够充分, 主要体现在:
2. 动态图的方法评估有问题: 一般的静态图会把, 比如一个图按照时间切分为 8:1:1 进行切分, 然后第一部分作为训练, 第二部分作为验证, 最后一部分作为测试, 但是这种评估方式是比较片面的.
ROLAND
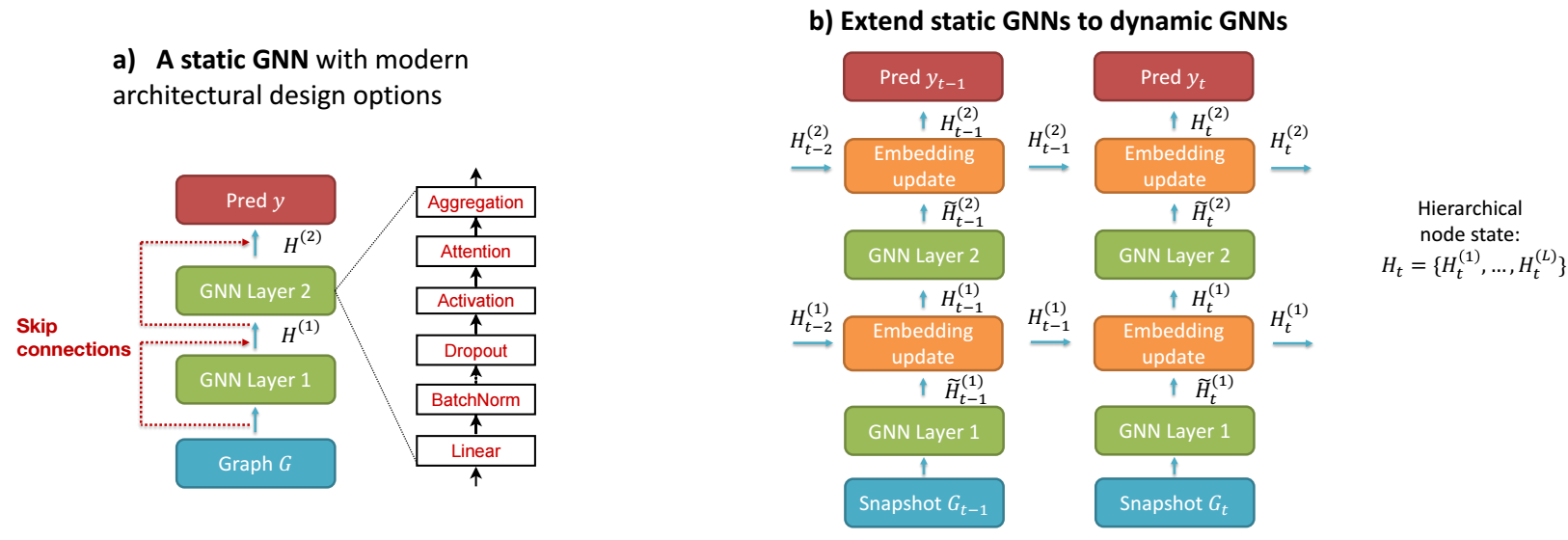1. 动态图上的图神经网络的设计缺少了对现有的静态图设计上的一些有点;
-
如上图所示, ROLAND 和以往的静态图上的主要区别在于 GNN layer 后多了一个 Embedding update 的模块, 这个模块以当前的 \(\tilde{H}_{t}^{(l)}\) 和历史的 \(H_{t-1}^{(l)}\) 为输入得到
\[H_{t}^{(l)} = \text{Update}^{(l)}(H_{t-1}^{(l)}, \tilde{H}_t^{(l)}), \]更新方式, 本文讨论了三种:
Moving Average:\[H_v^{(l)} = \kappa_t H_{t-1}^{(l)} + (1 - \kappa_t) \tilde{H}_t^{(l)}, \\ \kappa_t = \frac{ \sum_{\tau=1}^{t-1} |E_{\tau}| }{ \sum_{\tau=1}^{t-1}|E_{\tau}| + |E_t| } \in [0, 1]. \]MLP:\[ H_{t}^{(l)} = \text{MLP}( H_{t-1}^{(l)} \| \tilde{H}_t^{(l-1)} ). \]GRU(从给出的实验来看, 这个的效果似乎是最好的):\[ H_t^{(l)} = \text{GRU}( H_{t-1}^{(l)}, \tilde{H}_{t}^{(l)} ). \]
-
对于结点 \((u, v)\) 间的关系, 在时刻 \(t\) 出的预测可以是:
\[ y_t = \text{MLP}( h_{u, t}^{(L)} \| h_{v,t}^{(L)}, ) \quad \forall (u, v) \in V \times V. \]这里 \(L\) 是 GNN 的层数.
训练策略
-
在 \(t\) 时刻, 我们有了新的 graph snapshot \(G_t\), 我们不会回顾 \(G_1, G_2, \ldots, G_{t-1}\), 而仅仅保留:
\[\{H_{t-1}^{(l)}\}_{l=1}^{L} \]用于后续的训练, 于是乎, 每一阶段的训练都是非常高效的.
-
此外, 作者认为可以把每个 snapshot 看成是一个新的任务, 于是整个过程可以看成是一个多任务的过程. 作者引入 meta-learning 的思想, 维护一个 meta-model \(\text{GNN}^{meta}\), 作为每次新任务的模型的权重初始化, 然后该 meta model 按照如下方式进行更新:
\[ (1 - \alpha) \text{GNN}^{(meta)} + \alpha \text{GNN}, \alpha \in [0, 1]. \]
Live-update Evaluation
-
不同于之间的一次性的分割用于评测, 对于动态图, 作者提出采用如下的方式进行评测:
-
如上图所示, 在时刻 \(t\), 我们有历史信息 \(y_{t-1}\) 和当前与需要预测的信息 \(y_t\), \(y_{t-1}\) 分割为训练集和验证集, 然后得到最好的 checkpoint 并用于测试, 最后总的评价指标是所有的时刻的测试结果的平均 (有点赌博机的味道).
代码
[official]
