MMGCN: Multi-modal Graph Convolution Network for Personalized Recommendation of Micro-video
概
推荐领域里比较早的多模态方法.
符号说明
- \(\mathcal{U}\), user set;
- \(\mathcal{I}\), item set;
- \(m \in \mathcal{M} = \{v, a, t\}\), 某个模态 (\(v\) 表示 visual, \(a\) 表示 acoustic, \(t\) 表示 textual);
- \(\mathcal{G} = \{(u, i)| u \in \mathcal{U}, i \in \mathcal{I}\}\), user-item graph.
MMGCN
-
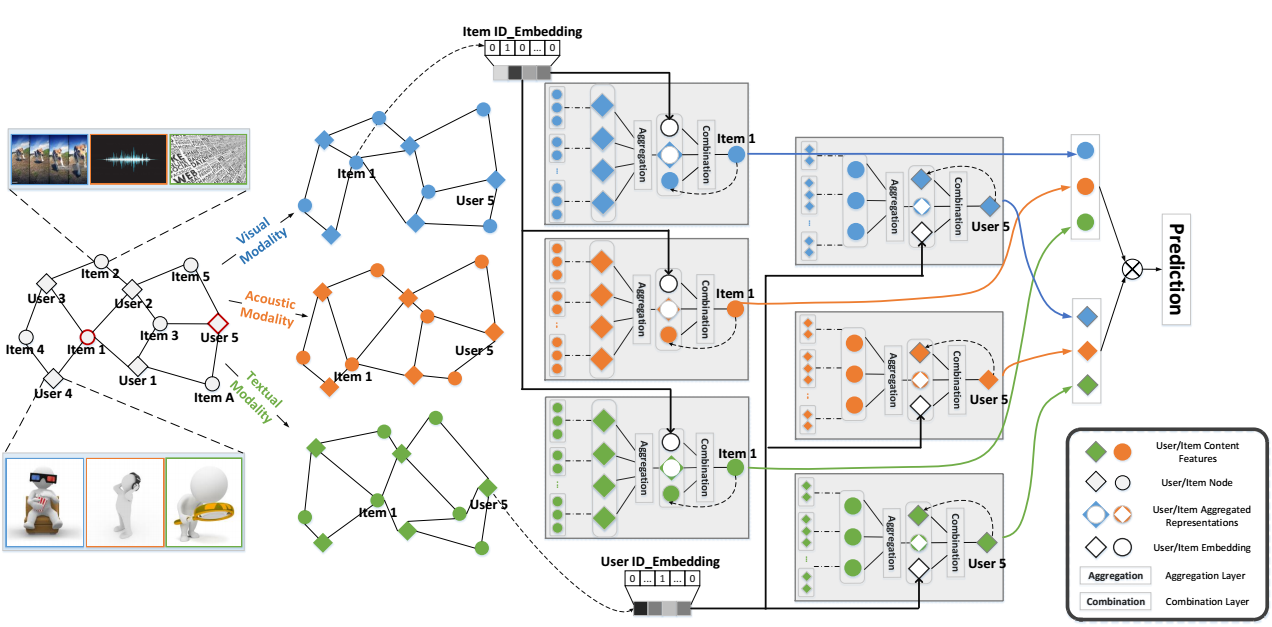
MMGCN 的思想很简单, 它对每一个模态都单独处理, 最后在汇总在一起得到 user/item 的表示.
-
初始情况下, 我们有:
\[ \mathbf{i}_m, \mathbf{u}_m, \mathbf{u}_{id}. \]其中 \(\mathbf{i}_m\) 是模态 \(m\) 的特征, 比如 \(m\) 是视频的使用, 可以是通过一些模型抽取得到的表征 (如用 ResNet50 对每一帧进行编码). \(\mathbf{u}_m\) 是用户在模态 \(m\) 处的表示 (应该是随机初始化然后再训练的吧?). \(\mathbf{u}_{id}\) 是用户的 id embedding.
-
MMGCN 的每一个 block 分为两步:
- aggregation:\[\mathbf{h}_m^{(l)} = f(\mathcal{N}_u), \]其中 \(f\) 可以是\[ f_{avg}(\mathcal{N}_u) = \text{LeakReLU}( \frac{1}{|\mathcal{N}_u|} \sum_{i \in \mathcal{N}_u} \mathbf{W}_{1, m}^{(l)} \mathbf{i}_m ), \]也可以是\[ f_{max}(\mathcal{N}_u) = \text{LeakReLU}( \max_{i \in \mathcal{N}_u} \mathbf{W}_{1, m}^{(l)} \mathbf{i}_m ). \]
- combination:\[ \mathbf{u}_m^{(l)} = g(\mathbf{h}_m^{(l)}, \mathbf{u}_m^{(l-1)}, \mathbf{u}_{id}). \]令\[ \mathbf{\hat{u}}_m = \text{LeakyReLU}( \mathbf{W}_{2,m}^{(l)} \mathbf{u}_m^{(l-1)} ) + \mathbf{u}_{id}, \]\(g\) 可以为如下的二者之一:\[g_{co}(\mathbf{h}_m, \mathbf{u}_m, \mathbf{u}_{id}) = \text{LeakyReLU}( \mathbf{W}_{3,m}^{(l)}( \mathbf{h}_m \| \mathbf{\hat{u}_m} ) ), \\ g_{ele}(\mathbf{h}_m, \mathbf{u}_m, \mathbf{u}_{id}) = \text{LeakyReLU}( \mathbf{W}_{3,m}^{(l)} \mathbf{h}_m + \mathbf{\hat{u}_m} ). \]
- aggregation:
-
最后
\[ \mathbf{u}^* = \sum_{m \in \mathcal{M}} \mathbf{u}_m^{(L)}, \mathbf{i}^* = \sum_{m \in \mathcal{M}} \mathbf{h}^{(L)}. \]注: 原文是 \(\mathbf{i}^* = \sum_{m \in \mathcal{M}} \mathbf{i}^{(L)}\), 但是并没有显式定义 \(\mathbf{i}^{(L)}\), 所以我的理解就是 \(\mathbf{h}^{(L)}\).
代码
[official]


