Convolutional Neural Networks on Graphs with Chebyshev Approximation, Revisited
概
作者剖析了 ChebNet 存在的一些缺陷, 并通过约束系数获得更好的性能.
符号说明
- \(V\), node set;
- \(E\), edge set;
- \(n = |V|\);
- \(\mathbf{X} \in \mathbb{R}^{n \times d}\), node features;
- \(\mathbf{A} \in \mathbb{R}^{n \times n}\), adjacency matrix;
- \(\mathbf{D}\), diagnoal degree matrix, \(\mathbf{D}_{ii} = \sum_{j} \mathbf{A}_{ij}\);
- \(\mathbf{P} = \mathbf{D}^{-1/2} \mathbf{A} \mathbf{D}^{-1/2}\), normalized adjacency matrix;
- \(\mathbf{L} = \mathbf{I} - \mathbf{D}^{-1/2} \mathbf{A} \mathbf{D}^{-1/2}\), normalized adjacency matrix;
- 假设\[\mathbf{L} = \mathbf{U} \Lambda \mathbf{U}^T. \]
Motivation
-
下面是常见的谱图网络的表达形式:
\[\mathbf{y} = \mathbf{U} \text{diag}(h(\lambda_1), \ldots, h(\lambda_n)) \mathbf{U}^T \mathbf{x} = \mathbf{U} h(\Lambda) \mathbf{U}^T \approx \sum_{k=0}^K w_k \mathbf{L}^k \mathbf{x}. \]其中 \(h(\cdot)\) 为 spectral filter, 而 \(w_k\) 表示则为系数. 上图中, \(h(\lambda) = \sum_{k=0}^K w_k \lambda^k\), 为 Monimal bases (单项式基).
-
ChebNet 采用的是 Chebyshev bases:
\[\mathbf{y} \approx \sum_{k=0}^K w_k T_k(\mathbf{\hat{L}}) \mathbf{x}, \quad \mathbf{\hat{L}} = 2 \mathbf{L} / \lambda_{max} - \mathbf{I}. \]其中
\[T_0(x) = 1, \\ T_1(x) = x, \\ T_k(x) = 2x T_{k-1}(x) - T_{k-2} (x). \]故, 对于 ChebNet 而言,
\[ h(\lambda) = \sum_{k=0}^K w_k T_k(\lambda). \] -
ChebNet, 理论上可以 cover 普通的 GCN, 同时应当具备更快的收敛速度, 可是相较于 Monomial 和 Bernstein bases 的方法, ChebNet 的效果却是最差的.
-
作者认为, 这是因为系数 \(w_k\) 学的不够好的原因:
-
理论上, 如果我们要用 Chebshev 基去逼近一个函数 \(f(x)\), 即找到 \(w_k\) 使得
\[f(x) = \sum_{k=0}^{\infty} w_k T_k(x), \]则 \(w_k\) 大体上应该按照 \(1/k^q\) 的速率下降.
-
诚然, \(w_k\) 是可学习的, 存在可能 \(w_k\) 学习到合适的权重, 但是实际上由于局部最优等问题, 可能并不会得到相应的结果, 作者做了一个小实验, 将 ChebNet 中的 \(w_k\) 替换为 \(w_k / k\), 即我们人为地进行缩放, 结果如下
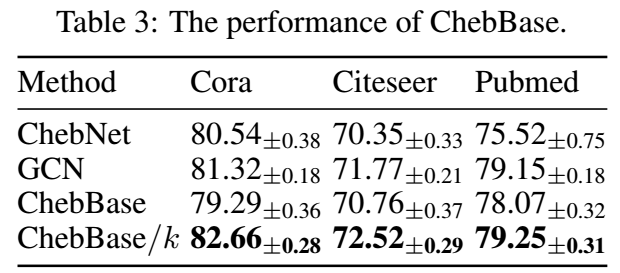
- 可以发现, 效果一下子有了不小地提升. 这说明, 如果我们不对系数加以限制, 仅凭梯度下降是不能够学习到合适的结果的.
ChebNetII
-
本文所提出的改进版本 ChebNetII:
\[ \mathbf{Y} = \sum_{k=0}^K \underbrace{\frac{2}{K+1} \sum_{j=0}^K \gamma_j T_k(x_j)}_{w_k} T_k(\mathbf{\hat{L}}) f_{\theta}(\mathbf{X}), \]实际上, 就是重参数化
\[ w_k = \frac{2}{K+1} \sum_{j=0}^K \gamma_j T_k(x_j). \]其中 \(\gamma_j\) 是可学习的参数, \(x_j, j=0,1,\ldots, K\) 为 Chebshev nodes:
\[ x_j = \cos(\frac{j + 1/2}{K + 1} \pi). \] -
这么做的原因是作者想套用 Chebyshev Interpolation, 其实相当于寄希望于 \(\gamma_j\) 能够学习到 \(h(x_j)\).a 这种表示方式有更快的收敛速度, 而且能够避免 Runge 问题. 不过, 我感觉是扯的有点远了.
代码
[official]
