How Powerful are Spectral Graph Neural Networks?

目录

Wang X. and Zhang M. How powerful are spectral graph neural networks? ICML, 2022.

概

分析谱图网络的表达能力.

符号说明

  • \(\kappa(M) = \frac{\lambda_{\max}}{\lambda_{\min}}\), 矩阵 \(M\) 的条件数;
  • \(\mathbb{V} = \{1, 2, \ldots, n\}\), node set;
  • \(\mathbb{E} \subset \mathbb{V} \times \mathbb{V}\), edge set;
  • \(X \in \mathbb{R}^{n \times d}\), node feature matrix;
  • \(\mathcal{G} = (\mathbb{V}, \mathbb{E}, X)\), graph;
  • \(N(i)\) 结点 \(i\) 的一阶邻居;
  • \(A \in \mathbb{R}^{n \times n}\) 邻接矩阵;
  • \(D\), degree matrix;
  • \(\hat{A} = D^{-1/2} A D^{-1/2}\), normalized adjacency matrix;
  • \(\hat{L} = I - \hat{A}\), normalized Laplacian matrix;
  • \(\hat{L} = U \Lambda U^T\), 特征分解.
  • \(\tilde{X} = U^T X\), 为信号 \(X\) 的 graph Fourier transform, 并有逆变换:

    \[X = U \tilde{X}. \]

Spectral GNN

  • 我们知道, Spectral GNN 的核心是 spectral filter

    \[\tag{1} U g(\Lambda) U^T X, \]

    其中 \(g: [0, 2] \rightarrow \mathbb{R}\) 多为 element-wise 的多项式算子 (注, \(\alpha_k\) 可以是超参数, 也可以是可学习的参数):

    \[g(\lambda) := \sum_{k=0}^K \alpha_k \lambda^k. \]

    此时, (1) 可以等价的写为:

    \[U g(\Lambda) U^T X = \sum_{k=0}^K \alpha_k \hat{L}^k X. \]

    大部分的 Spectral GNN 通过引入 MLP 和非线性激活函数, 可表达为:

    \[Z = \phi(g(\hat{L}) \varphi(X)). \]

  • 下面是一些常见的 \(g(\cdot)\).

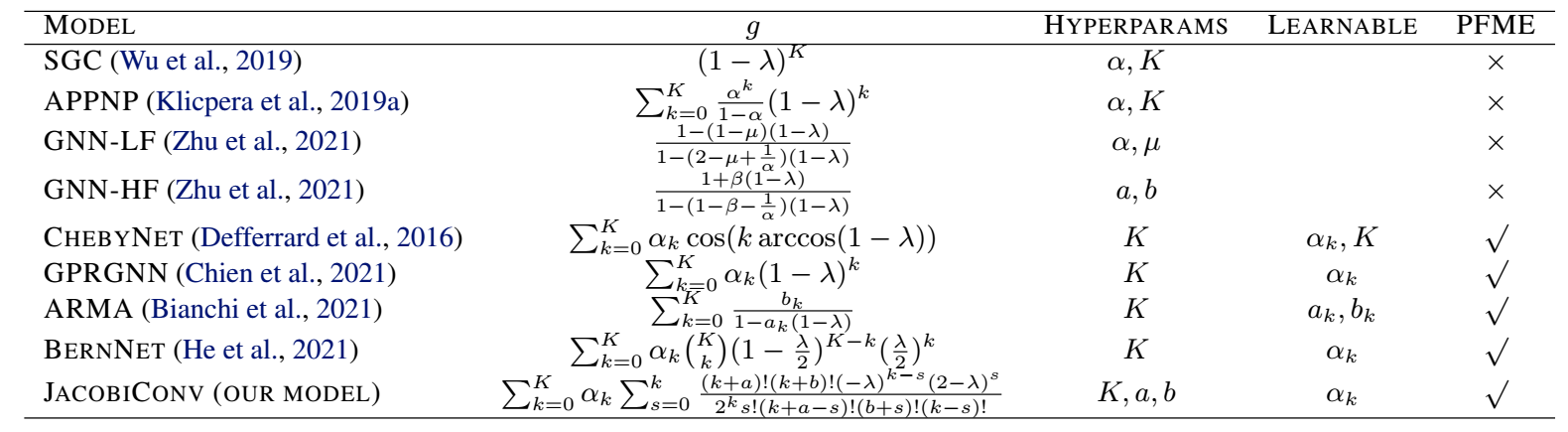
  • 下面我们主要分析 linear GNN

    \[\tag{2} Z = g(\hat{L}) XW \in \mathbb{R}^{d \times d'} \]

    的能力. 其中 \(X\) 是固定的, \(W \in \mathbb{R}^{d \times d'}\) 是可学习的参数.

  • 注意到,

    \[\tag{3} Z = g(\hat{L}) XW = U g(\Lambda) \tilde{X} W. \]

  • Theorem 4.1: 对于任意一维信号 \(z \in \mathbb{R}^n\), 我们均可以通过 linear GNN (2) 逼近, 若 \(\hat{L}\) 不存在重复的特征值, 且 \(X\) 包含所有频段的信号 (即不存在 \(\tilde{X}\) 有一行均为 0).

proof:

  • 我们要证明的是, 对于任意的一维信号 \(z \in \mathbb{R}^d\) 存在 \(w^* \in \mathbb{R}^d\) 和 \(g(\cdot)\) 使得

    \[Ug^*(\Lambda)\tilde{X} w^* = z \\ \Leftrightarrow g^*(\Lambda)\tilde{X} w^* = U^Tz. \\ \]

  • \(g(\Lambda)\) 是个对角矩阵, 根据多项式的性质, 它有着极为强大的拟合能力, 以

    \[g(\lambda) = \sum_{k=0}^{n-1} \theta_k \lambda^k \]

    为例, 此时我们有:

    \[\tag{4.1.1} g(\Lambda) = \text{diag}(B \Theta), \]

    其中

    \[B = [\lambda_i^{j-1}]_{ij}, \quad \Theta = [\theta_0, \ldots, \theta_{n-1}]. \]

    容易发现, \(B \in \mathbb{R}^{n \times n}\) 为范德蒙德矩阵, 当 \(\lambda_i \not= \lambda_j \forall i \not= j\) 成立的时候, \(B\) 可逆. 故

    \[v = B\Theta, \quad \forall v, \exist \Theta. \]

    现在我们把 (4.1.1) 拆解开来, 我们只需要证明:

    \[v_i (\tilde{X}_i^T w^*) = z_i, \forall i, \]

    即可, 倘若 \(\tilde{X}_i^T w^* \not=0 \quad \forall i\), 上面的证明就自然成立了. 对于任意 \(\tilde{X}\) 满足任一行均不全为 0, 我们都能找到这样的 \(w^*\). 令 \(V_i\) 为下列方程的解空间

    \[ \tilde{X}_i w = 0. \]

    容易发现 \(V_i\) 的维度为 \(n-1\). 只需取

    \[w^* \in \mathbb{R}^n \setminus \cup_{i=1}^n V_i, \]

    后者不为空集.

  • 很遗憾的是, 这个结论不能推广到多维信号的逼近上. 严格来说, 倘若 \(X\) 不是满秩的, 则对于任意的 \(d' > 1\), 存在 \(d'\)- 维的信号 \(Z\) 不能通过 linear gnn 完全逼近.

  • 故, 倘若想要拟合不同的信号, 最好的办法是应用多个独立的 filters.

  • 此外, 对于条件: \(X\) 包含所有频段的信号, 可以这么理解:

    • filter \(g(\cdot)\) 的作用实际上是对信号的缩放, 所以倘若 \(X\) 本身不包含那个频段的信息, 自然无法拟合对应频段的信号.

  • 需要一提的是, 倘若我们添加激活函数 \(\sigma(X)\), 某种程度上是能够缓解频段缺失的问题的.

Choice of Basis for Polynomial Filters

  • linear GNN 可以表述为如下的一般形式:

    \[\tag{7} Z = \sum_{k=0}^K \alpha_{k} g_{k}(\hat{L}) X W \]

    其中 \(g_k\) 代表多项式基.

  • 这里我们考虑如下的几种:

    • [Monomial]:

      \[g_k(\lambda) = \lambda^k. \]

    • [Chebyshev]:

      \[g_0(\lambda) = 1, \\ g_1(\lambda) = \lambda, \\ g_{n+1} (\lambda) = 2 \lambda g_n(\lambda) - g_{n-1}(\lambda). \]

    • [Bernstein]:

      \[g_k(\lambda) = g_{k,K}(\lambda) := \left ( \begin{array}{c} K \\ k \end{array} \right) \lambda^k (1 - \lambda)^{K-k}. \]

    • [Jacobi]:

      \[g_0^{a,b}(\lambda) = 1, \\ g_1^{a,b}(\lambda) = \frac{a-b}{2} + \frac{a + b + 2}{2} \lambda, \\ g_k^{a,b}(\lambda) = (\theta_k \lambda + \theta_k') g_{k-1}^{a, b}(\lambda) - \theta_k'' g_{k-2}^{a,b}(\lambda), \]

      其中

      \[\theta_k = \frac{(2k + a + b) (2k + a + b - 1)}{2k (k + a + b)}, \\ \theta_k' = \frac{(2k + a + b - 1) (a^2 - b^2)}{2k (k + a + b) (2k + a + b - 2)}, \\ \theta_k'' = \frac{(k + a - 1) (k + b - 1) (2k + a + b)}{k (k + a + b) (2k + a +b - 2)}. \]

  • 下面是作者给的一些例子:

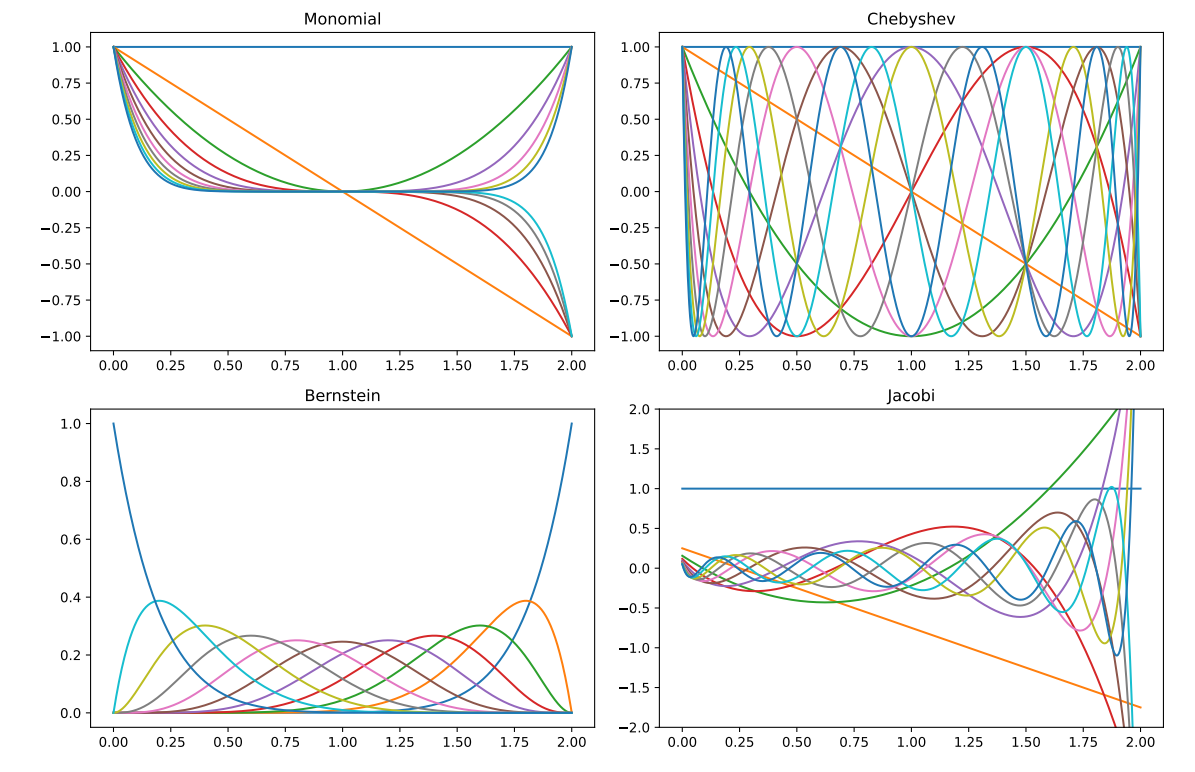
  • 下面是自己做的一些考察:



# %%

from typing import List
import torch
from freeplot import FreePlot


# %%


def mul(x, y):
    return x * y

def power_conv(
    zs: List[torch.Tensor], x, l: int
):
    if l == 0:
        return zs[0]

    assert len(zs) == l, "len(zs) != l for l != 0"

    return mul(x, zs[-1])

def legendre_conv(
    zs: List[torch.Tensor], x, l: int
):
    if l == 0:
        return zs[0]

    assert len(zs) == l, "len(zs) != l for l != 0"

    if l == 1:    
        return mul(x, zs[-1])
    else:
        part1 = (2 - 1 / l) * mul(x, zs[-1])
        part2 = (1 - 1 / l) * zs[-2]
        return part1 - part2

def chebyshev_conv(
    zs: List[torch.Tensor], x, l: int
):
    if l == 0:
        return zs[0]

    assert len(zs) == l, "len(zs) != l for l != 0"

    if l == 1:
        return mul(x, zs[-1])
    else:
        part1 = 2 * mul(x, zs[-1])
        part2 = zs[-2]
        return part1 - part2

def jacobi_conv(
    zs: List[torch.Tensor], x, l: int, 
    alpha: float = 1., beta: float = 1.
):
    if l == 0:
        return zs[0]

    assert len(zs) == l, "len(zs) != l for l != 0"

    if l == 1:
        c = (alpha - beta) / 2
        return c * zs[-1] + (alpha + beta + 2) / 2 * mul(x, zs[-1])
    else:
        c0 = 2 * l \
                * (l + alpha + beta) \
                * (2 * l + alpha + beta - 2)
        c1 = (2 * l + alpha + beta - 1) \
                * (alpha ** 2 - beta ** 2)
        c2 = (2 * l + alpha + beta - 1) \
                * (2 * l + alpha + beta) \
                * (2 * l + alpha + beta - 2)
        c3 = 2 * (l + alpha - 1) \
                * (l + beta - 1) \
                * (2 * l + alpha + beta)
        
        part1 = c1 * zs[-1]
        part2 = c2 * mul(x, zs[-1])
        part3 = c3 * zs[-2]

        return (part1 + part2 - part3) / c0

def run(x, conv_fn, L):
    zs = [torch.ones_like(x)]
    for l in range(1, L + 1):
        zs.append(conv_fn(zs, x, l))
    return zs

# %%

from functools import partial

L = 5
x = torch.linspace(-1, 1, 100)
alpha = 1
beta = 1

fp = FreePlot(
    (1, 4),
    titles=("Monomial", "Legendre", "Chebyshev", "Jacobi"),
    sharey=False
)

for l, z in enumerate(run(x, power_conv, L)[1:], start=1):
    fp.lineplot(x, z, label=f"Layer: {l}", index=(0, 0), marker='')

for l, z in enumerate(run(x, legendre_conv, L)[1:], start=1):
    fp.lineplot(x, z, label=f"Layer: {l}", index=(0, 1), marker='')

for l, z in enumerate(run(x, chebyshev_conv, L)[1:], start=1):
    fp.lineplot(x, z, label=f"Layer: {l}", index=(0, 2), marker='')

jacobi_conv_ = partial(jacobi_conv, alpha=alpha, beta=beta)
for l, z in enumerate(run(x, jacobi_conv_, L)[1:], start=1):
    fp.lineplot(x, z, label=f"Layer: {l}", index=(0, 3), marker='')

fp.legend(0.2, 0.99, ncol=L)
fp.set_title()
fp.show()
  • 对于 Jacobi 多项式基, 我们可以调节 \(\alpha, \beta\) 来调节对高频低频的一个侧重度:

  • 作者证明了, 在特殊的情况下 (也不算特别特殊), Jacobi 多项式基的系数 \(\alpha_k\) 相较于其它的多项式基的系数更容易收敛.

JacobiConv

  • 一般来说, \(\alpha_k\) 随着 \(k\) 增加是逐渐减小的 (绝对值), 故而直接学习可能得不到想要的结果. 所以作者把它们重参数化为:

    \[\alpha_k = \beta_k \prod_{i=1}^k \gamma_i, \]

    其中 \(\gamma_i = \gamma' \tanh(\eta_i)\) 用来保证:

    \[\gamma_i \in [-\gamma', \gamma']. \]

  • 最终的公式可以改写为:

    \[P_k^{a, b}(\hat{A}) \hat{X} = \gamma_k \theta_k \hat{A} P_{k-1}^{a, b} (\hat{A}) \hat{X} + \gamma_k \theta_k' P_{k-1}^{a, b}(\hat{A}) \hat{X} - \gamma_k \gamma_{k-1} \theta_k'' P_{k-2}^{a, b}(\hat{A}) \hat{X}. \]

代码

[official]

posted @ 2023-11-20 20:37  馒头and花卷  阅读(70)  评论(0)  编辑  收藏  举报