Recurrent Marked Temporal Point Processes: Embedding Event History to Vector
概
利用 RNN 学习强度函数 \(\lambda^*\). 在往下阅读前, 请确保对 Temporal Point Process 有一定的了解.
Motivation
-
在日常生活中, 常常有这样的需求, 知道过往的一些事件 (及其发生的时间), 希望预测下一发生的事件 (及其发生的时间).
-
严格来说, 我们有序列:
\[\mathcal{S} = [(t_1, y_1), (t_2, y_2), \ldots, (t_n, y_n)], \]我们希望预测: \((t_{n+1}, y_{n+1})\).
-
通常来说, 我们会有多个序列
\[\mathcal{C} = \{\mathcal{S}^1, \mathcal{S}^2, \ldots\}, \]此为拟合模型所需的数据集.
-
TPP (Temporal Point Process) 就是解决这个问题的一个工具, 它需要给定强度函数:
\[\lambda^*(t, y) = \lambda^*(t) \cdot f^*(y|t). \]注: 这里 \(*\) 表示以 \(\mathcal{H}_{t^-} = \{(t_i, y_i): t_i < t\}\) 为条件.
-
有了强度函数后, 我们便可以求得密度函数:
\[f^*(t, y) = p(t_{n+1}=t, y_{n+1}=y| \mathcal{H}_{t_n}) = \bigg( \lambda^* \exp\big(- \int_{t_n}^t \lambda^*(\tau) \mathrm{d} \tau \big) \bigg) \cdot f^*(y|t). \] -
传统的关于 \(\lambda^*(t, \kappa)\) 的设计主要在于 \(\lambda^*\) 的设计:
- Hawkes process:\[\lambda^*(t) = \gamma_0 + \alpha \sum_{t_j < t} \gamma(t, t_j). \]
- Self-correcting process:\[\lambda^*(t) = \exp(\mu t - \sum_{t_i < t} \alpha). \]
- Hawkes process:
-
它们存在一些问题:
- \(\lambda^*(t)\) 是固定的, 所以往往仅适用于一些特定的任务;
- \(f^*(y|t)\) 的设计往往特别简单.
-
本文希望通过神经网络 (RNN) 来拟合 \(\lambda^*(t)\), 从而 TPP 更具普适性.
Marked Temporal Point Process
-
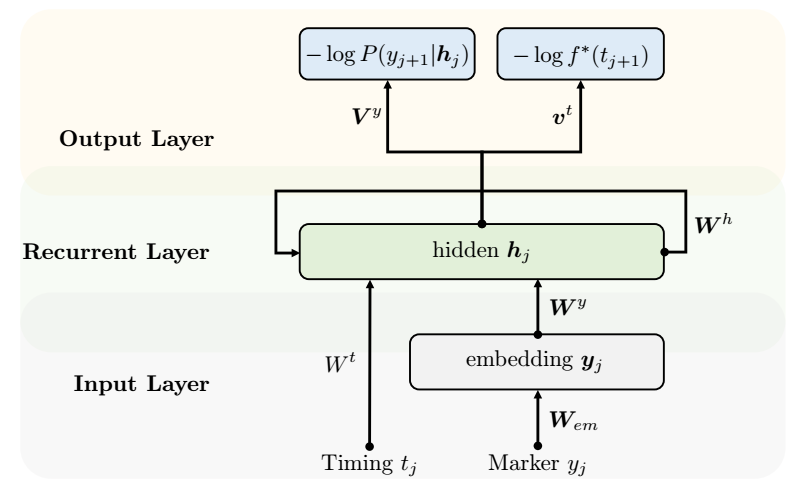
思想很简单, 假设我们现在要预测 \((t_{j+1}, y_{j+1})\).
-
假设 \(\mathcal{H}_{t_{j-1}}\), 即历史信息已经融入到了隐向量 \(\bm{h}_{j-1}\) 中.
-
给定当前的事件 \((t_j, y_j)\), 得到它们的 embedding 表示 \(\bm{t}_j, \bm{y}_j\).
-
则当前时刻的信息建模为:
\[\bm{h}_j = \max\{ \bm{W}^y \bm{y}_j + \bm{W}^t \bm{t}_j + \bm{W}^h \bm{h}_{j-1} + \bm{b}_h, 0 \}. \] -
定义:
\[\mathbb{P}(y_{j+1}=k|t_{j+1}, \mathcal{H}_j) =f^*(y_{j+1}|t_{j+1}) = \frac{ \exp(\bm{V}_{k, :}^y \bm{h}_j + b_k^y) }{ \sum_{k=1}^K \exp(\bm{V}_{k, :}^y \bm{h}_j + b_k^y) } \]实际上就是一个 \(K\) 类的分类 (这里我们假设事件类型是有限的).
-
然后:
\[\lambda^*(t) := \exp \bigg( \underbrace{{\bm{v}^t}^T \cdot \bm{h}_j}_{past influence} + \underbrace{w^t (t - t_j)}_{current influence} + \underbrace{b^t}_{base intensity} \bigg). \] -
一个比较好的消息是, 上面的函数关于 \(t\) 是容易积分的, 这使得我们可以很容易地球密度函数:
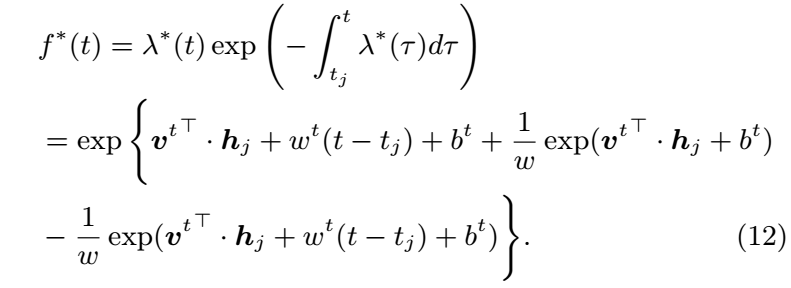
-
于是, 我们可以通过极大化对数似然进行优化:
\[\sum_i \sum_j \bigg( \log P(y_{j+1}^i | \bm{h}_j) + \log f(d_{j+1}^i | \bm{h}_j) \bigg). \] -
注: 在推理的时候, 作者采用
\[\hat{t}_{j+1} = \mathbb{E}_{f^*}[t] = \int_{t_j}^{\infty} t \cdot f^*(t) \mathrm{d}t \]作为下一时刻的估计. 这里需要通过数值方法近似. (Q: 为啥不用最大概率作为估计呢?)
代码
[official]


