Linkless Link Prediction via Relational Distillation

目录

• 概
• 符号说明
• LLP
• 代码

Guo Z., Shiao W., Zhang S., Liu Y., Chawla N. V., Shah N. and Zhao T. Linkless link prediction via relational distillation. ICML, 2023.

概

从 GNN 教师模型蒸馏到 MLP 学生模型.

符号说明

• $G = (\mathcal{V, E})$, 无向图;
• $\mathbf{A} \in \{0, 1\}^{N \times N}$, 邻接矩阵;
• $\mathbf{X} \in \mathbb{R}^{N \times F}$, node features;
• $\mathcal{E}^- = (\mathcal{V} \times \mathcal{V}) \setminus \mathcal{E}$.
• $\mathbf{H} \in \mathbb{R}^{N \times D}$, 结点表示.

LLP

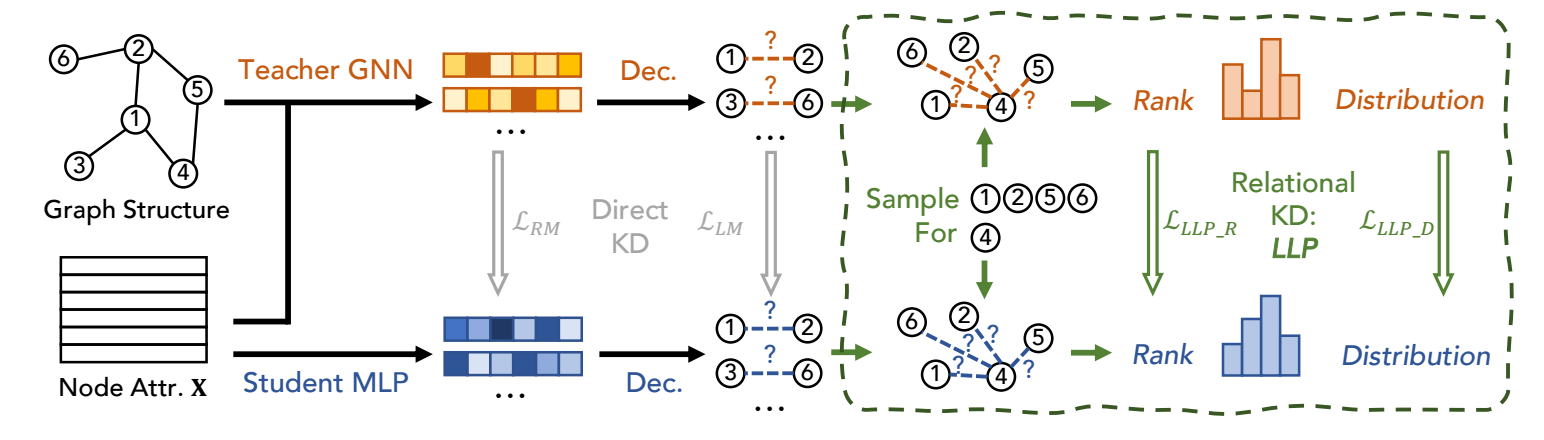
• LLP 假设教师模型是一个 GNN 模型 (因为通过它所得的结点表示有比较好的结构信息), 然后希望通过蒸馏将这些信息蒸馏给学生模型.

• 想法很简单, 令:

  $$\hat{y}_{ij} = \sigma(\text{Decoder}(\bm{h}_i, \bm{h}_j))$$

  为对结点 $v_i, v_j$ 间存在边的概率预测. 通过下面的两种方式, 拉近教师模型和学生模型的分布.

• Rank-based Matching:

  $$\mathcal{L}_{LLP\_R} = \sum_{v \in \mathcal{V}} \sum_{\hat{y}_{v, i}, \hat{y}_{v, j}} \max(0, -r \cdot (\hat{y}_{v, i} - \hat{y}_{v, j}) + \delta),$$

  其中

  $$r = \left \{ \begin{array}{ll} 1 & \text{ if } y_{v,i}^t - y_{v,j}^t > \delta, \\ -1 & \text{ if } y_{v,i}^t - y_{v,j}^t < -\delta, \\ 0 & \text{ otherwise}. \end{array} \right.$$

  想法其实很简单, 就是要求学生模型模型教师模型的排序 (以一定的 margin $\delta$), 如果不满足给予一定的惩罚.

• Distribution-based Matching:

  $$\mathcal{L}_{LLP\_D} = \sum_{v \in \mathcal{V}} \sum_{i \in \mathcal{C}_v} \frac{\exp (y_{v, i}^t / \tau)}{\sum_{j \in \mathcal{C}_v} \exp (y_{v, j}^t / \tau)} \log \frac{\exp (\hat{y}_{v, i} / \tau)}{\sum_{j \in \mathcal{C}_v} \exp (\hat{y}_{v, j} / \tau)}.$$

  即一般的 logits 的蒸馏. $\mathcal{C}_v$ 是需要采样的, 以免过多的计算量. 采样方式如下:

  1. 通过随机游走采样局部近似的点, 记为 $\mathcal{C}_v^N$;
  2. 随机采样结点, 记为 $\mathcal{C}_v^R$;
  3. 最后 $\mathcal{C}_v = \mathcal{C}_v^N \cup \mathcal{C}_v^R$.

• 最后的训练损失为:

  $$\mathcal{L} = \alpha \cdot \mathcal{L}_{sup} + \beta \cdot \mathcal{L}_{LLP\_R} + \gamma \cdot \mathcal{L}_{LLP\_D}.$$

代码

[official]