Decoupled Knowledge Distillation
Zhao B., Cui Q., Song R., Qiu Y. and Liang J. Decoupled knowledge distillation. CVPR, 2022.
概
对普通的 KD (Knowledge Distillation) 损失解耦得到 Target Class Knowledge Distillation (TCKD) 和 Non-target Class Knowledge Distillation (NCKD) 两部分. 由此提出新的蒸馏损失以强化 NCKD 部分
符号说明
-
\(\mathbf{z} \in \mathbb{R}^C\) 为 logits, \(C\) 表示类别个数;
-
正常的概率估计:
\[p_i = \frac{\exp(z_i)}{\sum_{j=1}^C \exp(z_j)}, i=1,2,\ldots, C. \] -
二分概率估计:
\[\mathbf{b} = [p_t, p_{\setminus t}], \: p_{\setminus t} = \sum_{i\not=t} \frac{\exp(z_i)}{\sum_{j=1}^C \exp(z_j)} \] -
Non-target 上的概率分布:
\[\tilde{p}_i = \frac{\exp(z_i)}{\sum_{j\not= t} \exp(z_j)}, \quad i=1,2,\ldots, t-1, t+1, \ldots, C. \] -
显然有:
\[\tag{1} p_i = p_{\setminus t} \cdot \tilde{p}_i, \quad i \not = t. \]
DKD
-
令 \(p^{\mathcal{T}}, p^{\mathcal{S}}\) 分别表示 teacher, student 的概率分布, 则一般的蒸馏损失为:
\[\text{KD} = \text{KL}(\mathbf{p}^{\mathcal{T}}\| \mathbf{p}^{\mathcal{S}}) = p_t^{\mathcal{T}} \log (\frac{p_t^{\mathcal{T}}}{p_t^S}) + \sum_{i\not=} p_i^{\mathcal{T}} \log (\frac{p_i^{\mathcal{T}}}{p_i^{\mathcal{S}}}). \] -
将 (1) 代入其中可以得到:
\[\text{KD} = \underbrace{p_t^{\mathcal{T}} \log (\frac{p_t^{\mathcal{T}}}{p_t^{\mathcal{S}}}) +p_{\setminus t}^{\mathcal{T}} \log (\frac{p_{\setminus{t}}^{\mathcal{T}}}{p_{\setminus{t}}^{\mathcal{S}}})}_{\text{KL}(\mathbf{b}^{\mathcal{T}}\| \mathbf{b}^{\mathcal{S}})} + p_{\setminus t}^{\mathcal{T}} \underbrace{\sum_{i=1, i\not=t}^C \tilde{p}_i^{\mathcal{T}} \log (\frac{\tilde{p}_i^{\mathcal{T}}}{\tilde{p}_i^{\mathcal{S}}})}_{\text{KL}(\mathbf{\tilde{p}}^{\mathcal{T}}\| \mathbf{\tilde{p}}^{\mathcal{S}})}. \] -
故:
\[\text{KD} = \underbrace{\text{KL}(\mathbf{b}^{\mathcal{T}}\| \mathbf{b}^{\mathcal{S}})}_{=: \text{TCKD}} + (1 - p_t^{\mathcal{T}}) \underbrace{\text{KL}(\mathbf{\tilde{p}}^{\mathcal{T}}\| \mathbf{\tilde{p}}^{\mathcal{S}})}_{=: \text{NCKD}}. \] -
TCKD 关注 target 的概率的差异, 而 NCKD 则是反映了在 non-target class 中的一个一致性.
-
这里需要关注的一个点是 NCKD 的权重 \((1 - p_t^{\mathcal{T}})\), 显然, 当教师模型对当前的分类特别自信的时候 (即 \(p_t^{\mathcal{T}} \rightarrow 1\)), NCKD 的权重大大降低了. 不过, 作者认为, 这个时候, NCKD 实际上也是很重要的.
-
其次, \((1 - p_t^{\mathcal{T}})\) 这个系数有时候不能够很好的反应难度, 显然, 当类别数很多的时候, \(p_{t}^{\mathcal{T}}\) 就很难接近 1.
-
总之, 作者希望更加灵活地控制调节这两个部分:
\[\text{DKD} = \alpha \text{TCKD} + \beta \text{NCKD}. \] -
此外, 作者做了一些很有意思的实验:
-
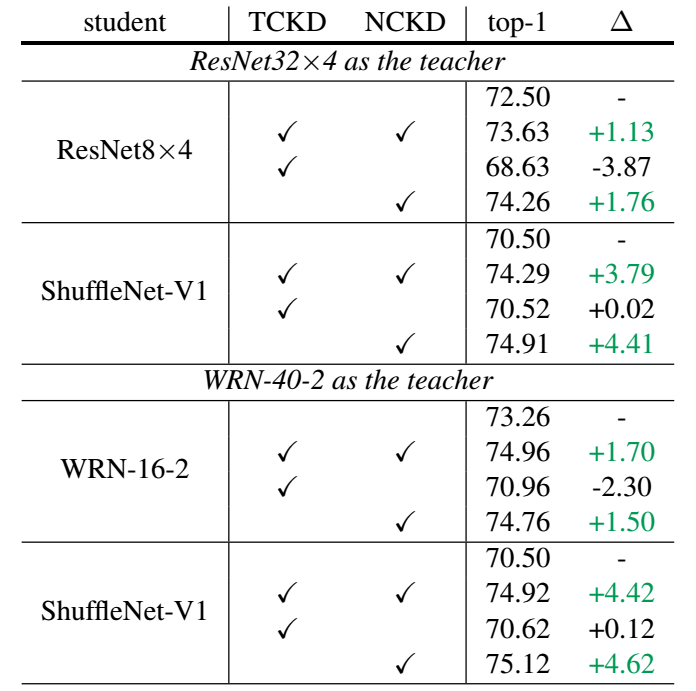
如上图所示, 仅 NCKD 即可媲美 KD, 这说明 KD 中实际效果大抵来源于 NCKD 部分. 比如, 作者通常设置 \(\alpha=1, \beta=8\) 以达到最佳的性能.
-
其实, 总的来看, KD 里的 temperature 其实起到的是一个类似的作用, 某种程度上, 它把 \(p_t^{\mathcal{T}}\) 降低从而加重了 NCKD 部分.
代码
[official]
