BWT and FM-index
概
有趣的编解码.
Burrows-Wheler Transform (BWT)
- BWT 的目的是把普通的字符串转换成重复率更高的字符串, 从而更易于压缩. 为了方便解释, 下面会用字符串 'abaaba' 来进行解释 (虽然它 BWT 编码后的结果并没有体现出易于压缩的特性).
编码
- 首先在字符串最后加上 '$' (这只是一个象征符号, 要求是它的字典序先于其它的字符), 得到 'abaaba$';
- 接着, 得到这个字符串所有的 rotations:
abaaba$ baaba$a aaba$ab aba$aba ba$abaa a$abaab $abaaba - 然后按照字典序排序可以得到:
$abaaba a$abaab aaba$ab aba$aba abaaba$ ba$abaa baaba$a - 分别记第一列和最后一列为
则 L 就是 'abaaba' 的 BWT.F = $aaaabb L = abba$aa,
性质
-
F 可以通过对 L 按照字典序进行排序得到.
-
倘若我们对 'abaaba' 中的相同字符进行区分, 比如:
\[abaaba \rightarrow a_0b_0a_1a_2b_1a_3. \]此时我们有
可以发现, F, L 中 a/b 的序实际上一致的. -
这个性质其实是由理论保证的:
-
即, F/L 中相同字符的序用相同块所决定, 故而它们的序是一致的.
-
通过这一性质, 我们可以方便地通过 L 来恢复出原先地字符串.
-
接下来, 我们稍微将一些为什么 BWT 往往可能会比原字符串更容易压缩, 设想如果一个非常非常长的字符串中频繁出现 'the', 则就会有很多的 't' 由于 'hexxxxxxxxt' 的排序聚在一块:
s = 'the_small_or_the_big_or_the_large_or_the_huge_man' l = 'neeeelegerrrmml_hhhgghiurtttt_bl_as_a___oooa____$h'
解码
- 通过如下方式, 我们可以倒着恢复出原先的字符串 (从 '$' 开始):
-
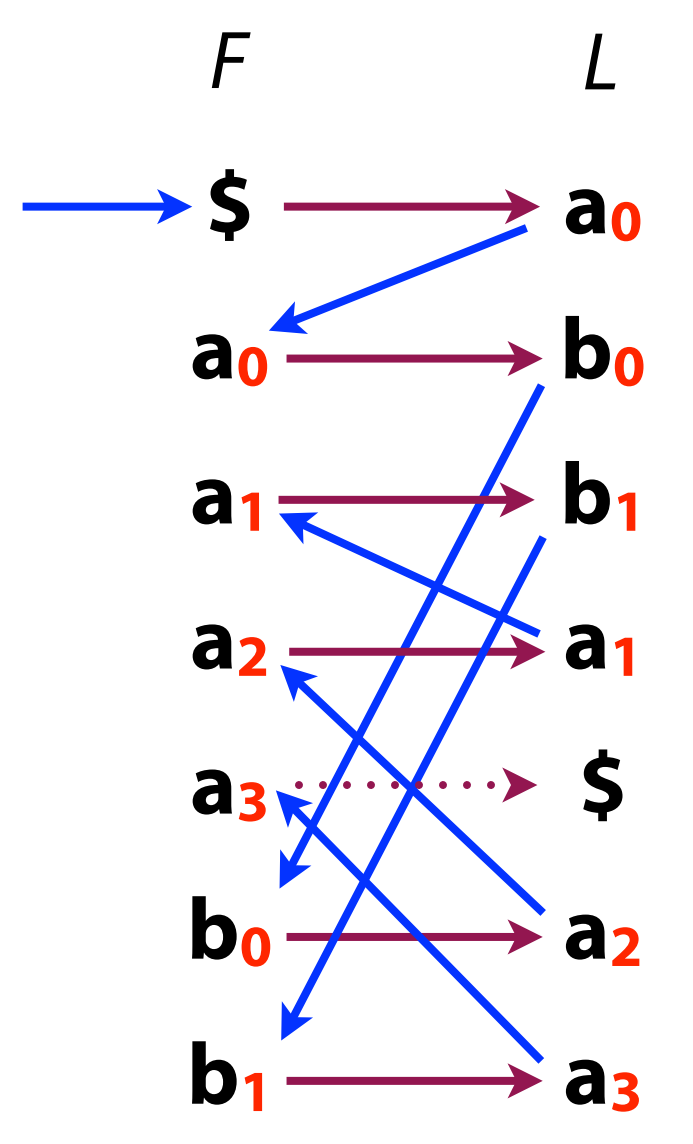
大家可能会疑惑 (至少我一开始有这个疑惑), 如果不知道原先的字符串 'abaaba', 我们怎么按照图中方式排序呢? 实际上, 具体的序不重要, \(a_0b_0a_1a_2b_1a_3\) 还是 \(a_0b_1a_2a_3b_0a_5\) 都不重要, 重要的是这个序能够唯一确定这个字符即可.
-
所以你完全可以给 \(L\) 弄一个例如 [0, 1, 2, 3, 4, 5, 6] 的序.
-
当然, 在对 L 排序得到 F 的过程还是得按照字典序来, 下面的代码采取的是一种比较方便的排序方式: 即对 \(L\) 中的每种元素从 0 开始排序 (主要这么做, 可以方便地对 F 进行索引).
-
比如, 假设我们假设 L 中 a 的元素共有 \(n_a\) 个, 则我们按照它们在 L 中出现的顺序为它们排序:
\[a_0, a_1, \ldots, a_{n_a - 1}. \] -
现在, 假设我们当前处理的行数为 \(r\), 此时 L 对应的元素为 \(a_{i_r}\), 则下一行行数为:
\[r' = \zeta[a] + i_r. \]这里 \(\zeta[a]\) 表示的元素 \(a\) 在 F 中第一次出现的位置 (从 0 开始计数). 对于 'abaaba' 这个例子, \(\zeta[a] = 1\) (因为最开始的时 '$'), 然后 \(\zeta[b]=5\).
FM-index
-
FM-index 主要是基于 BWT 提供了一种快速查找子字符串的方法, 比如我们想知道 'aba' 在 'abaaba' 中出现的位置 (即 0 和 3 (匹配字符串首个字符的位置)). FM-index 提供了一种非常简便和高效的方式去实现这一点.
-
明确: 解决这个问题需要匹配字符串的同时确定位置.
直观但简陋的方式
-
既然 BWT 是从后往前恢复的, 我们也如此进行匹配.
-
'aba' 的最后一个字符为 'a', 于是我们先从 F 中找到 'a' 所对应的行:
-
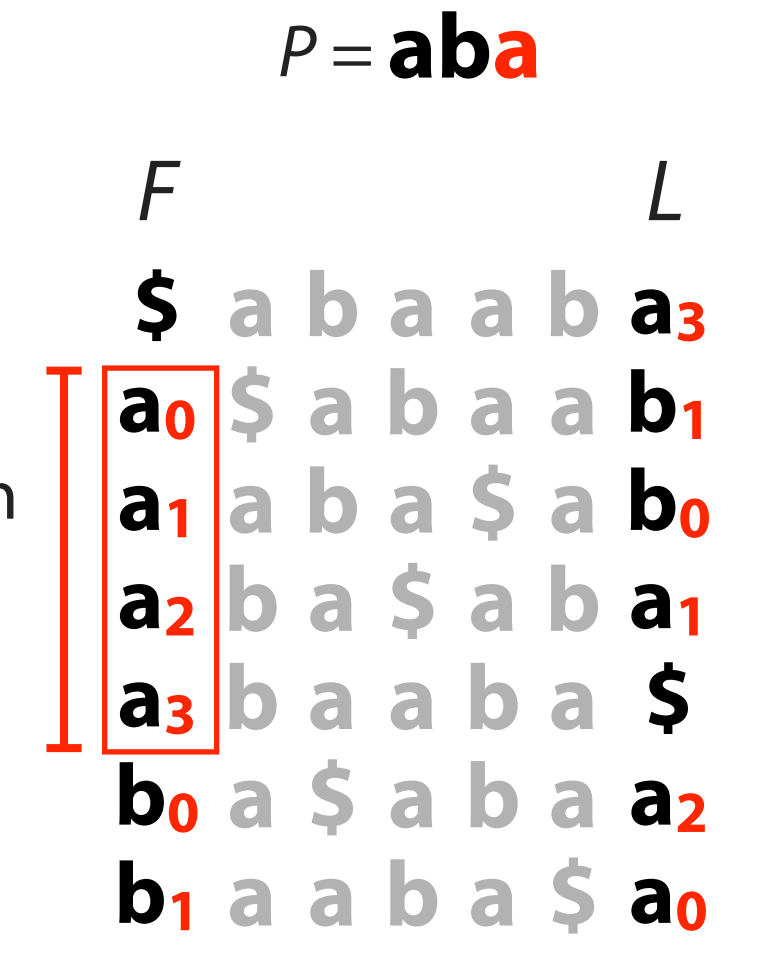
我们知道, 这些行对应 L 处的元素就是出现在 'a' 之前的元素, 所以接下来我们需要确定这些行处, 且 L 位置对应元素为 'b' 的行 (我们找到了 \(b_0, b_1\)):
-
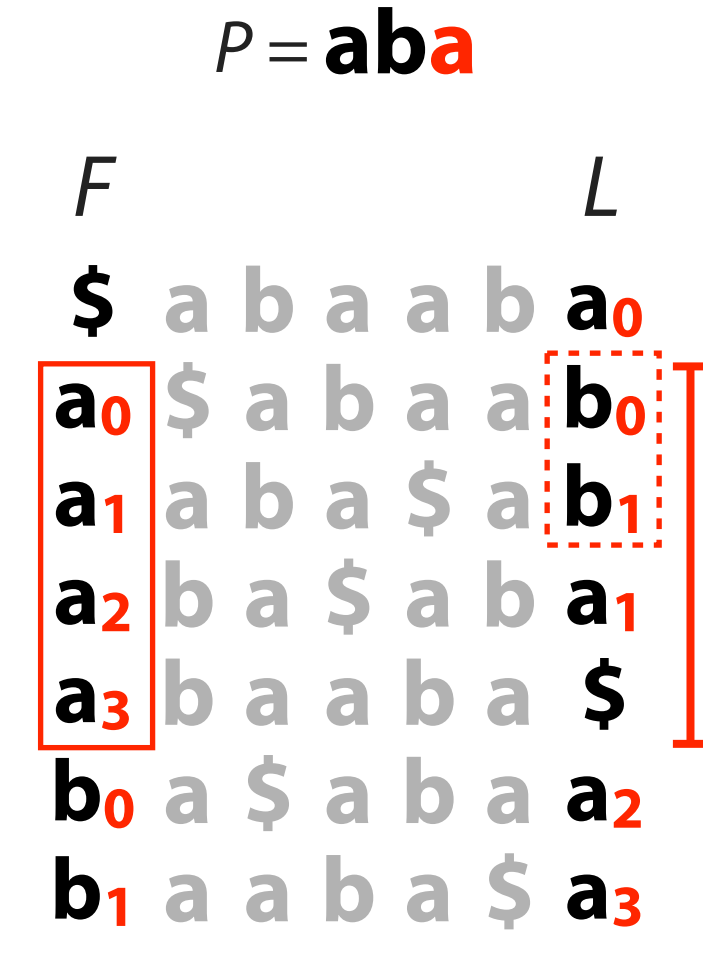
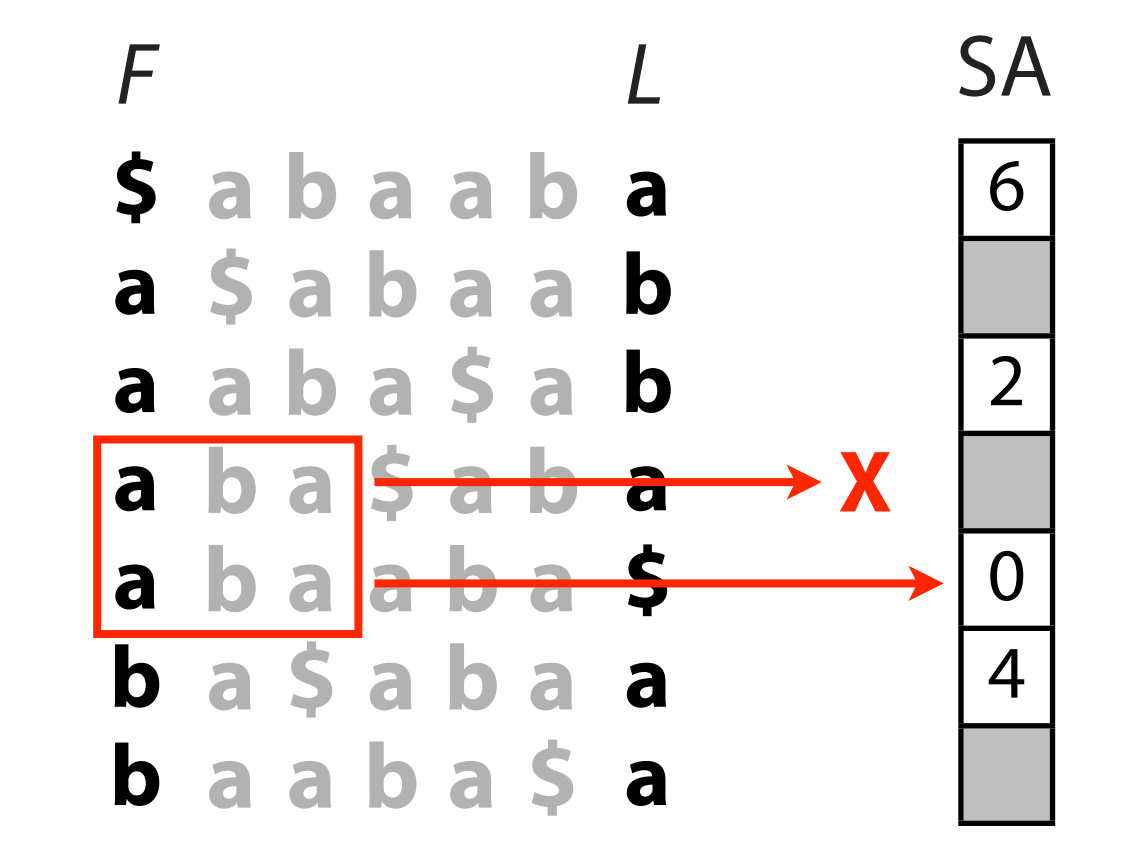
接下来, 我们要找到 \(b_0, b_1\) 在 F 中的对应的行 (这可以通过上面介绍的方式实现):
-
然后判断那些行之后 L 的位置处是否为 'a' (为了匹配 'aba'):
-
我们发现, \(a_2, a_3\) 是匹配的, 此时匹配部分已经完成了, 接下来我们要做的就是找到 \(a_2, a_3\) 在原字符串中的位置 (对应 3 和 0).
更高效的方式
-
虽然上述方式问题能够解决我们的问题, 但是它的时间和空间复杂都比较高, 存在很大的优化空间.
-
可以发现, 在匹配部分, 核心问题是: 在 F 列上确定对应的行后, 如果快速在那些行中确定所需元素出现的位置.
-
FM-index 的方法如下图所示:
-
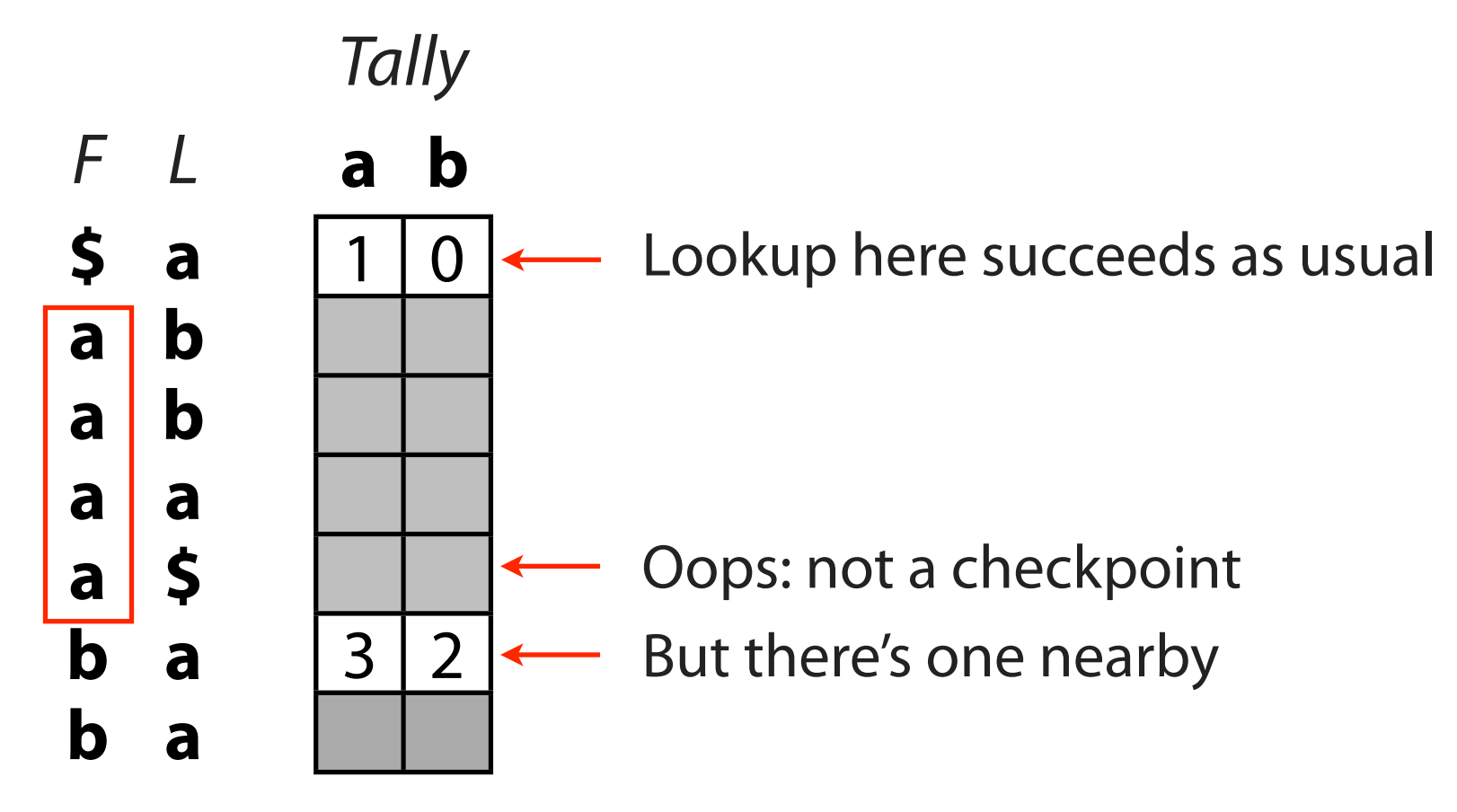
我们在 F 中 'a' 块前后设置检查点, 检查点统计了截至目前检查点各元素的出现次数. 则两次检查点元素 'b' 出现次数之差就是 'ba' 出现的次数.
-
让我们一般化一点, 假设两个检查点间的区域就是我们感兴趣的搜索区域, 我们希望搜索在该区域中元素 'x' 的序.
-
假设两次检查点 'x' 的出现次数分别为 \(c, c'\), 则显然
\[x_{c}, x_{c+1}, \ldots, x_{c'-1} \]恰好出现在这个区域中. 由此, 我们可以很容易地推断出它们在 F 中出现的位置:
\[\zeta[x] + c, \zeta[x] + c + 1, \ldots, \zeta[x] + c' - 1. \] -
另一个问题是匹配好字符串找位置.
-
此时, 我们可以保存部分的位置, 其它元素的位置可以通过'附近'元素很容易地推断出来, 这里就不细讲了.
代码
from collections import defaultdict
class BWT:
@classmethod
def encode(cls, s: str):
r"""
Encode a string into BWT.
Parameters:
-----------
s: str
Returns:
--------
l: str
"""
s = s + '$'
ss = s * 2
table = sorted([ss[i:i+len(s)] for i in range(len(s))])
return ''.join(map(lambda x: x[-1], table))
@classmethod
def _specify_order(cls, l: str):
r"""
Determine the order for each character in l and count their frequency.
Returns:
--------
orders: List, the same size as `l`
counts: Dict, the frequency for each character
"""
counts = defaultdict(int)
orders = []
for c in l:
orders.append(counts[c])
counts[c] += 1
return orders, counts
@classmethod
def _specify_start(cls, counts: dict):
r"""
Determine the first row a character appears.
Returns:
--------
firsts: Dict, the first row a character appears
"""
starts = {}
start = 0
for c, count in sorted(counts.items()):
starts[c] = start
start += count
return starts
@classmethod
def decode(cls, l: str):
r"""
Recover the original string from BWT.
Parameters:
-----------
l: str, BWT
Returns:
--------
s: str
"""
orders, counts = cls._specify_order(l)
starts = cls._specify_start(counts)
s = '$'
row = 0
cur = l[row]
while cur != '$':
s = cur + s
row = starts[cur] + orders[row]
cur = l[row]
return s[:-1]
