UniKGQA Unified Retrieval and Reasoning for Solving Multi-hop Question Answering Over Knowledge Graph
概
统一: 从知识图谱中检索出相关的子图, 并在子图中进行推理.
主要内容
-
我们有知识图谱 \(\mathcal{G} = \{\langle e, r, e' \rangle| e, e' \in \mathcal{E}, r \in \mathcal{R}\}\), 其中 triple \(\langle e, r, e' \rangle\) 表示存在关系 \(r\) 于头实体 \(e\) 和尾实体 \(e'\) 之间.
-
我们的任务是给定问题 \(q\), 然后根据只是图谱找到相应的答案 \(\{e\}\) (即, 答案是某些实体).
-
之前的方法是:
- 先从知识图谱中采样一个和问题 \(q\) 相关的子图 \(\mathcal{G}_q\);
- 在子图 \(\mathcal{G}_q\) 上进行推理.
-
由于两个模块的独立性, 导致训练并不充分, 所以作者希望将二者耦合在一起, 仅有部分参数不同.
-
首先, 将 \(\mathcal{G}\) 转换为 abstract graph \(\tilde{\mathcal{G}}\):
- 对于头实体 \(e\) 和关系 \(r\), 可能有多个尾实体 \(e'\) 满足 \(\langle e, r, e' \rangle\), 将他们融合为一个点:\[\tilde{e} = \{e'| \langle e, r, e' \rangle \in \mathcal{G}\}; \]
- 对于关系 \(r\) 和尾实体 \(e'\), 类似融合头实体;
- 下面是一个例子:
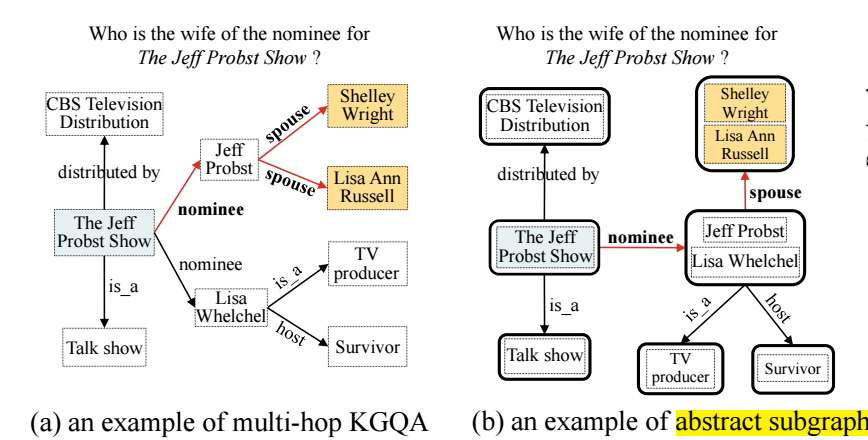
- 对于头实体 \(e\) 和关系 \(r\), 可能有多个尾实体 \(e'\) 满足 \(\langle e, r, e' \rangle\), 将他们融合为一个点:
-
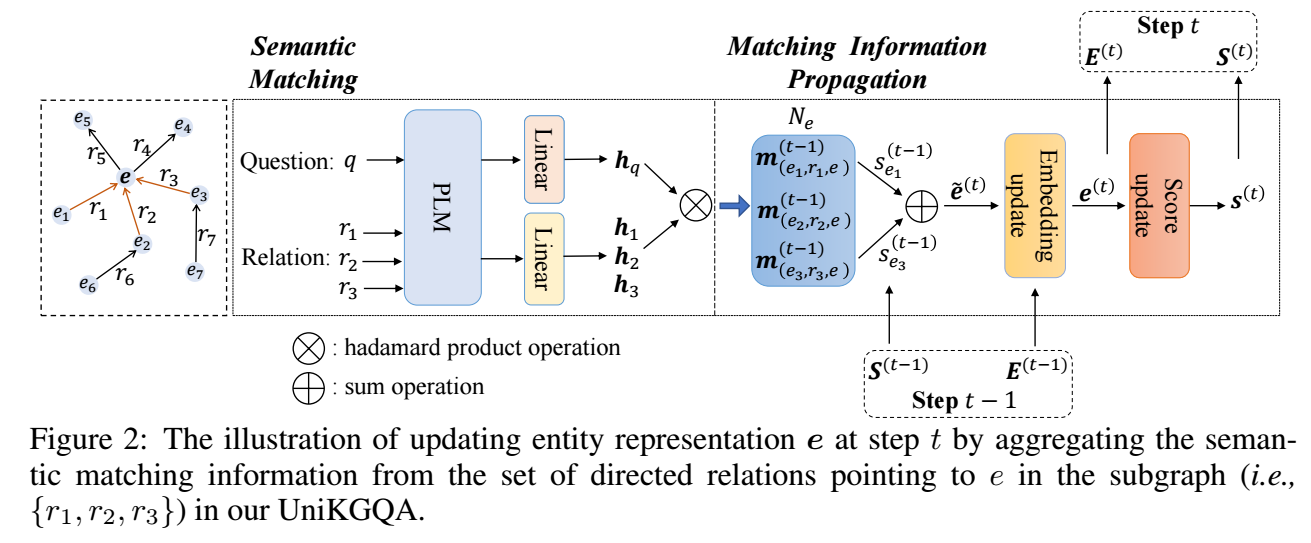
现在, 假设们有一个和 \(q\) 相关的子图 \(\mathcal{G}_g\) (对于 retrieval 阶段 \(\mathcal{G}_g\) 为 abstract graph, 对于 reasoning 阶段为从检索阶段得到的子图), 我们做如下推理:
-
Semantic Matching: 利用 PLM (预训练模型) 去编码 \(q, r\) 上的 texts:
\[\bm{h}_q = \text{PLM}(q), \quad \bm{h}_r = \text{PLM}(r). \]然后, 计算 triple 的特征 (但是似乎和 \(e, e'\) 无关):
\[\bm{m}_{\langle e', r, e \rangle}^{(t)} = \sigma(\bm{h}_q \bm{W}_Q^{(t)} \odot \bm{h}_r \bm{W}_R^{(t)}). \] -
Matching Information Propagation: 通过一般的 GNN 对结点进行更新:
\[\bm{e}^{(t)} = \bm{W}_E^{(t)} \bigg(\bigg[ \bm{e}^{(t-1)}; \sum_{\langle e', r, e \rangle \in \mathcal{N}_e} s_{e'}^{(t-1)} \cdot \bm{m}_{\langle e', r, e\rangle}^{(t)} \bigg]\bigg), \\ \bm{s}^{(t)} = \text{softmax}({\bm{E}^{(t)}}^T \bm{v}). \]其中 \(\bm{s} = [s_{e}]\) 为每个结点的 score (越高和问题的相关度越好).
-
注: 还有一些初始化和训练的东西, 这里就不讲了. 总而言之, 这篇论文的推理还是需要检索的, 只是两个阶段的训练变得互相影响了.
代码
[official]


