Robust Graph Representation Learning via Neural Sparsification
概
自动稀疏化图的, 思想很简单, 就是学一个概率分布然后用 Gumbel-softmax 采样.
符号说明
- \(n\) 个结点的图;
- \(G = (V, E, \mathbf{A})\), 图;
- \(V \in \mathbb{R}^{n \times d_n}\), 每一行是对应结点的特征;
- \(E \in \{0, 1\}^{n \times n}\), 邻接矩阵, \(E(u, v) = 1\) 若存在边 \((u, v)\);
- \(\mathbf{A} \in \mathbb{R}^{n \times n \times d_e}\), \(\mathbf{A}(u, v)\) 表示边 \(e_{uv}\) 所对应的边的特征.
NeuralSparse
-
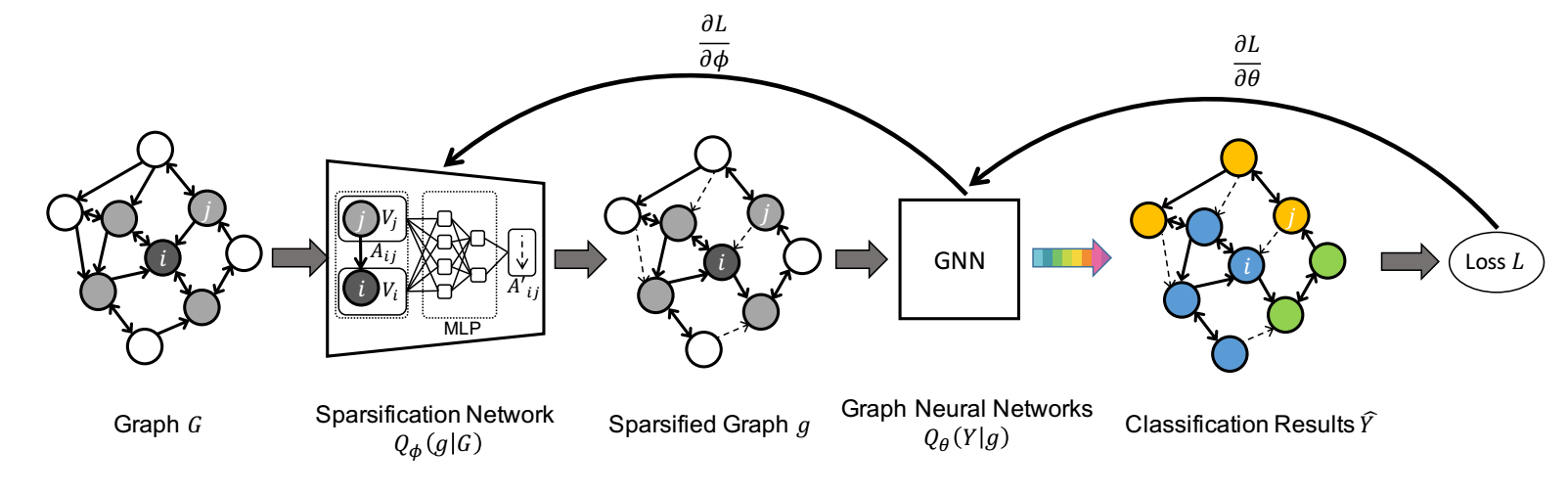
图上的任务可以归结为估计概率分布:
\[P(Y|G), \]如果是 node-level 的分类任务, 则 \(Y \in \mathbb{R}^{n \times c}\), 若是 graph-level 的分类任务, 则 \(Y \in \mathbb{R}^c\).
-
作者认为:
\[P(Y|G) = \sum_{g \in \mathbb{S}_G} P(Y|g, G) P(g |G) \approx \sum_{g \in \mathbb{S}_G} P(Y|g) P(g |G). \]即, 稀疏化后的 graph \(g\) 包含了大部分预测 \(Y\) 所需的信息.
-
作者的想法很简单, 就是用:
\[P(g | G) \rightarrow Q_{\phi}(g|G), \\ P(Y | g) \rightarrow Q_{\theta}(Y|g). \]\(Q_{\phi}\) 实际上是一个稀疏化网络, \(Q_{\theta}\) 实际上是在空间 \(\mathbb{S}_G\) 上的一个分类网络.
-
针对稀疏化, 作者首先选择了一个非常简单的 \(\mathbb{S}_G\), 作者假设稀疏化后的图每个结点只有 \(k\) 个邻居, 整体的稀疏化过程如下:
-
即, 通过一个简单的 MLP 来预测出边 \((u, v)\) 的 logit, 然后通过 gumbel-softmax 进行采样.
-
\(Q_{\theta}\) 就是一般的图网络.
