Weighted Nonlocal Laplacian on Interpolation from Sparse Data
概
针对 graph laplacian 提出的一个改进, 方法很简单, 但是切入点不错.
符号说明
- \(P = \{\bm{p}_1, \ldots, \bm{p}_n\} \subset \mathbb{R}^{d}\), a set of points;
- \(S = \{\bm{p}_1, \ldots, \bm{s}_m\} \subset P\), a subset of \(P\);
- \(u: P \rightarrow \mathbb{R}\), 定义在点集 \(P\) 上的一个函数;
WNLL
-
假设 \(u\) 在子集 \(S\) 上的值我们已经知道了, 即:
\[u(\bm{s}) = g(\bm{s}), \quad \forall s \in S, \]我们希望借此来推断出 \(u\) 在 \(P \setminus S\) 上的值.
-
一般来说, 我们会采用如下的方法来估计:
\[\begin{array}{rl} \min_{u} & \mathcal{J}(u) = \bm{u}^TL \bm{u} = \frac{1}{2} \sum_{\bm{x}, \bm{y} \in P} w(\bm{x}, \bm{y}) (u(\bm{x} - u(\bm{y})))^2, \\ \text{s.t.} & u(\bm{x}) = g(\bm{x}), \quad \bm{x} \in S. \end{array} \]这里 \(\bm{u} = [u(1), \ldots, u(n)]^T\), 而 \(L\) 为 \(P\) 上的拉普拉斯矩阵, 它定义为:
\[L = D - W, \quad W_{ij} = w(\bm{p}_i, \bm{p}_j). \]一般来说, 我们常常采用如下方式估计权重:
\[w(\bm{x}, \bm{y}) := \exp(- \frac{\|\bm{x} - \bm{y}\|^2}{\sigma^2}). \] -
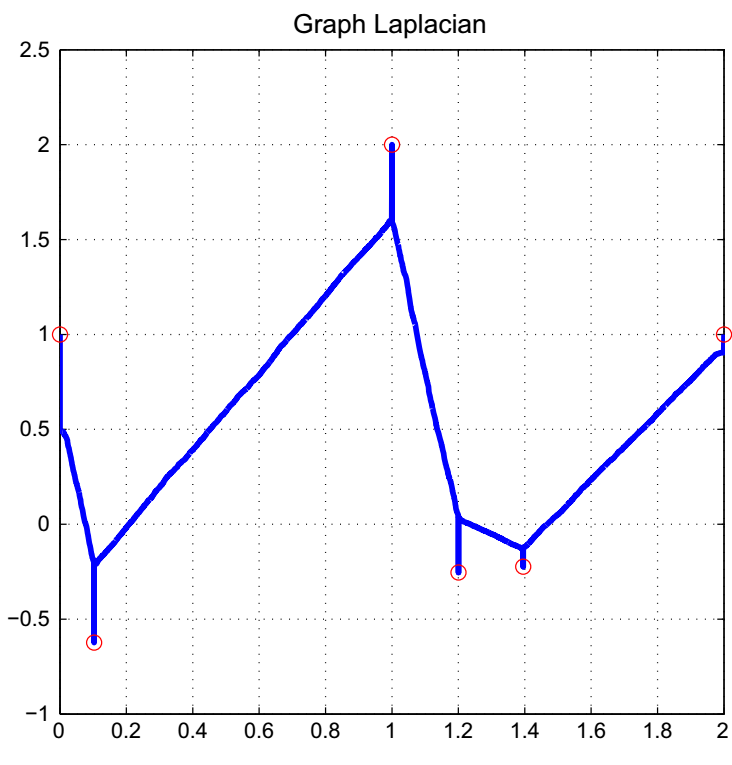
但是这种方法存在一个问题, 作者举了一个例子:
- \(P\) 为 \((0, 2)\) 上的 5000 个点;
- 假设我们知道其中 6 个点, 通过优化上述问题得到的解如下:
-
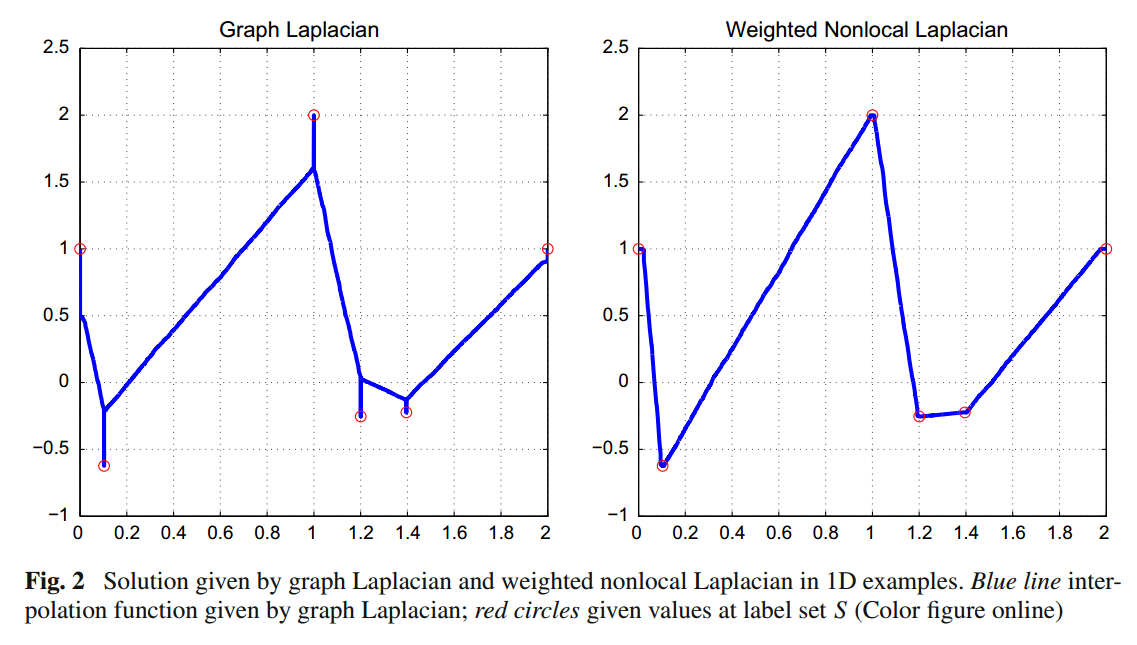
可以发现, 得到的近似值 \(\hat{\bm{u}}\) 在已知的那些点的地方是十分不连续的. 本文的问题背景其实比较偏图像补全, 这就导致对不连续点十分敏感, 所以需要解决这个问题.
-
实际上, 我们可以发现:
\[\mathcal{J}(u) = \sum_{\bm{x} \in P \setminus S} \bigg( \sum_{\bm{y} \in P} w(\bm{x}, \bm{y}) (u(\bm{x}) - u(\bm{y}))^2 \bigg) + \sum_{\bm{x} \in S} \bigg( \sum_{\bm{y} \in P} w(\bm{x}, \bm{y}) (u(\bm{x}) - u(\bm{y}))^2 \bigg). \]通常 \(|S| \ll |P|\), 故第二项其实每一项的值的误差不小, 相对于占比更多的第一项还是微不足道的, 所以优化总的损失的时候第二项总是会被轻视.
-
故, 作者做出了如下的改进:
\[\mathcal{J}_{WNLL}(u) = \sum_{\bm{x} \in P \setminus S} \bigg( \sum_{\bm{y} \in P} w(\bm{x}, \bm{y}) (u(\bm{x}) - u(\bm{y}))^2 \bigg) + \mu \cdot \sum_{\bm{x} \in S} \bigg( \sum_{\bm{y} \in P} w(\bm{x}, \bm{y}) (u(\bm{x}) - u(\bm{y}))^2 \bigg). \]且推荐 \(\mu\) 取
\[|P| / |S|. \]可以认为是对数据不平衡的一个纠正. 当 \(|S| \ll |P|\) 的时候, 一个较大的权重会被施加.
-
注, 本文是从 point integral method 角度切入分析的, 但是我对那块不是很了解, 这里还是放一个简单的版本吧.
-
下图是一个图像不全的例子 ((a) 原图; (b) 采样的点; (c) 普通的 graph lapalcian; (d) WNLL):
-
不过, 不要太被吓到, 毕竟很难相信 (b) 能够恢复出来 (d), 作者这里用到的点集, 其中 \(\bm{p}\) 不是位置坐标, 而是周围的一个 patch, 所以 \(W\) 中实际上蕴含了很多图的信息.
-
还有一个之前的例子:
