Graph-less Collaborative Filtering
Xia L., Huang C., Shi J. and Xu Y. Graph-less collaborative filtering. WWW, 2023.
概
从 GNN 的教师模型中蒸馏结构信息到一般的不带图结构的学生模型中去.
符号说明
-
\(\{u_1, u_2, \ldots, u_I\}\), users;
-
\(\{v_1, v_2, \ldots, v_J\}\), items;
-
\(\mathbf{A} \in \mathbb{R}^{I \times J}\), interaction matrix, \(a_{ij} = 1\) 表示观测到的, 否则为 0.
-
\(\mathbf{\bar{h}}\), 初始 embedding;
-
\(y_{ij}\), \(u_i, v_j\) 的分数;
-
教师模型:
\[y_{ij} = \mathbf{h}_i^T \mathbf{h}_j, \: \mathbf{H} = \text{G-Embed}(\mathcal{G}, \mathbf{\bar{H}})= (\text{Agg}(\text{Prop}(\mathcal{G}, \mathbf{\bar{H}})))^L. \] -
学生模型:
\[y_{ij} = \mathbf{h}_i^T \mathbf{h}_j, \: \mathbf{h}_i = \text{M-Embed}(\mathbf{\bar{h}}_i), \mathbf{h}_j = \text{M-Embed}(\mathbf{\bar{h}}_j). \] -
\(\text{G-Embed}, \text{M-Embed}\) 分别是 GNN 和普通的 MLP.
SimRec
-
我们的教师模型, 具体的 embedding 部分为:
\[\mathbf{H}^{(t)} = \sum_{l=0}^L \mathbf{H}_l^{(t)} \in \mathbb{R}^{(I+J) \times d}, \quad \mathbf{H}_{l+1}^{(t)} = \mathbf{D}^{-1/2} (\mathbf{\bar{A}} + \mathbf{I}) \mathbf{D}^{-1/2} \cdot \mathbf{H}_l^{(t)}. \] -
学生模型的 embedding 的具体结构为:
\[\mathbf{h}_i^{(s)} = \text{FC}^{L'}(\mathbf{\bar{h}}_i^{(s)}) = \delta(\mathbf{W} \mathbf{\bar{h}}_i^{(s)}) + \mathbf{\bar{h}}_i^{(s)} \in \mathbb{R}^{d}. \]其中 \(\delta(\cdot)\) 表示 LeakyReLU.
Prediction-Level Distillation
-
均匀采样 triplets \(\mathcal{T}_1 = \{(u_i, v_j, v_k)\}\), 然后
\[z_{i, j, k} = y_{ij} - y_{ik} = \mathbf{h}_i^T \mathbf{h}_j - \mathbf{h}_i^T \mathbf{h}_k. \] -
这部分的蒸馏损失为:
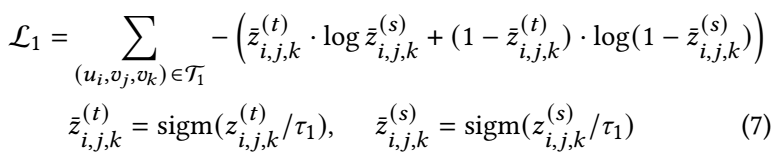
-
其中 \(\text{sigm}\) 表示 sigmoid 激活函数, \(\tau_1\) 表示 temperature factor. 显然, 这部分实际上就是要求学生模型的预测差异尽可能去接近教师模型的预测差异.
Embedding-level Distillation
-
这部分采用普通的对比损失 InfoNCE, 要求学生模型的 embedding 尽可能和对应的教师模型的高阶信息接近, 而和其它的远离:

-
注意到, 我们仅仅利用教师模型中的 \(\sum_{l=2}^L \mathbf{h}_{l}^{(t)}\) 部分, 以期吸收高阶信息.
Adaptive Contrastive Regularization
-
设计这部分损失, 作者主要是希望促使 embedding 不要收到 over-smoothing 的影响, 于是:
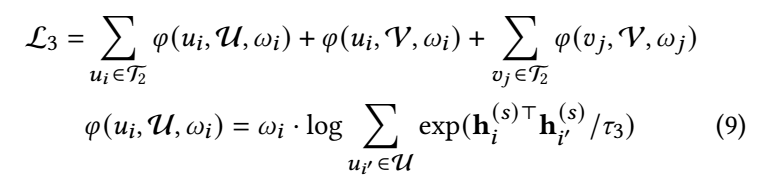
-
其中, 权重 \(\omega_i\) 定义为:

总的损失
-
首先对于教师模型采用普通的 BPR loss.
-
对于学生模型, 采用如下的损失训练:
\[\mathcal{L}^{(s)} = \mathcal{L}_{rec} + \lambda_1 \mathcal{L}_1 + \lambda_2 \mathcal{L}_2 + \lambda_3 \mathcal{L}_3 + \lambda_4 \mathcal{L}_4, \\ \mathcal{L}_{rec} = -\sum_{(u_i, v_j) \in \mathcal{\mathcal{T}_2}} y_{ij},\quad \mathcal{L}_4 = \|\mathbf{\bar{H}}^{(s)}\|_F^2. \]其中 \(\mathcal{T_2} = \{(u, v)\}\) 为 observed pairs.
代码
[official]


