Knowledge Distillation from A Stronger Teacher
概
用 Pearson correlation coefficient 来替代一般的 KL 散度用于蒸馏.
DIST
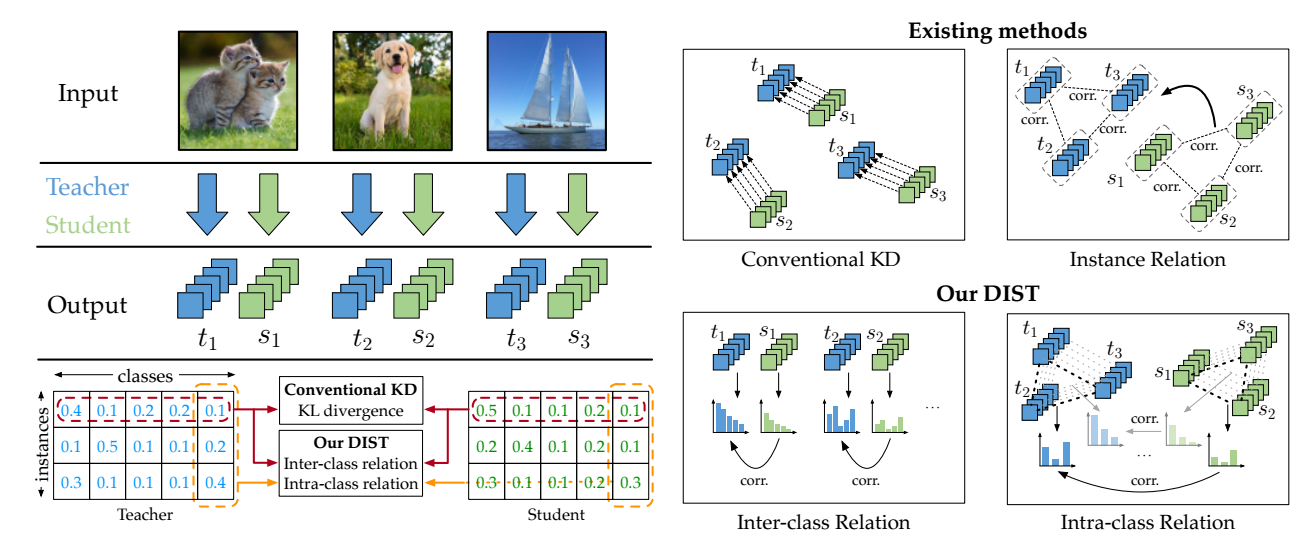
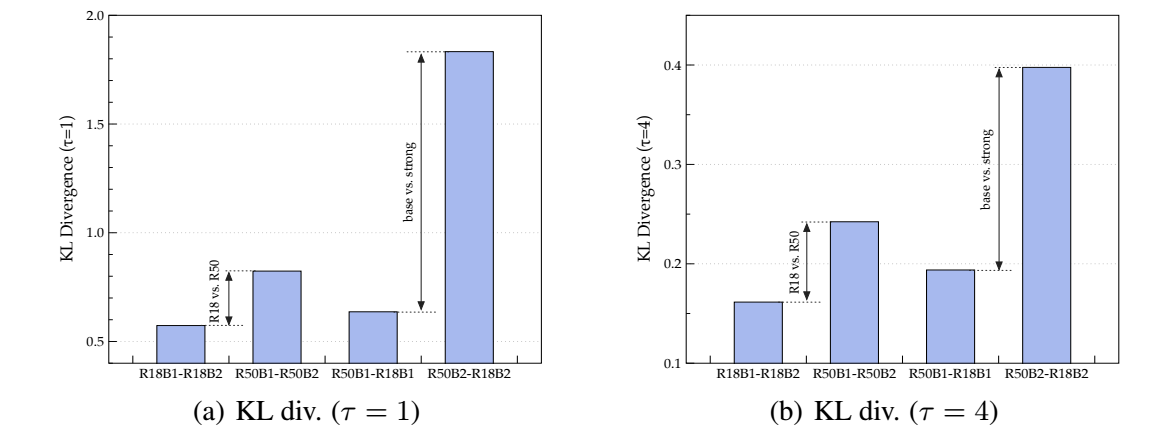
- 首先, 作者针对不同的 model size ResNet18, Resnet50 和不同的训练策略 B1, B2 (B2 更复杂一点, 通过 B2 训练得到的模型一般效果更好一点) 训练得到不同的教师模型. 比较在这些不同的教师模型的监督下, 学生模型训练后和教师模型的 KL 散度的差异:
-
可以发现, 有如下的结论:
- 在相同的策略下, 教师和学生的模型差距越大, 最后的 KL 散度越大;
- 在相同的模型大小下, 用更复杂的策略训练得到差距更大.
-
需要知道, KL 散度越大, 说明学生难以模仿教师的输出, 这启发作者抛弃传统的 KL 散度, 转向更简单更一般的对齐方式.
-
KL 散度要求学生的输出分布和教师的分布尽可能一致, 而 DIST 仅要求二者是线性相关即可, 即:
\[d_p(\bm{u}, \bm{v}) := 1 - \rho_p (\bm{u}, \bm{v}), \quad \rho_p(\bm{u}, \bm{v}) := \frac{\text{Cov}(\bm{u}, \bm{v})}{\text{Std}(\bm{u}) \text{Std}(\bm{v})}, \]尽可能小.
-
假设 \(\bm{Y}^{(t)}, \bm{Y}^{(s)} \in \mathbb{R}^{B \times C}\) 分别为教师和学生模型的输出概率, \(B, C\) 分别是 batchsize 和 类别数目.
-
DIST 考虑类间和类内的线性相关性, 即:
\[\mathcal{L}_{intra} := \frac{1}{C} \sum_{j=1}^C d_p (\bm{Y}_{:, j}^{(s)}, \bm{Y}_{:, j}^{(t)}), \quad \mathcal{L}_{inter} := \frac{1}{B} \sum_{i=1}^B d_p (\bm{Y}_{i, :}^{(s)}, \bm{Y}_{i, :}^{(t)}). \] -
最后的训练学生模型的损失为:
\[\mathcal{L}_{tr} = \alpha \mathcal{L}_{cls} + \beta \mathcal{L}_{inter} + \gamma \mathcal{L}_{intra}. \]
代码
[official]
