Topology Distillation for Recommender System
Kang S., Hwang J., Kweon W. and Yu H. Topology distillation for recommender system. KDD, 2021.
概
一种基于关系的知识蒸馏, 这种关系的处理比较特殊.
Topology Distillation
-
已经有很多蒸馏的文章指出, 受限于学生模型的表达能力, 让其完全模仿教师模型的输出有些过于勉强和死板. 很多后续的文章都尝试提出一些`统计性'的指标, 从而给予学生模型更简单但有效的目标.
-
本文实际中是从关系角度出发的, TD 希望学生模型的 embedding 的关系和教师模型的 embedding 的关系能够尽可能的一致.
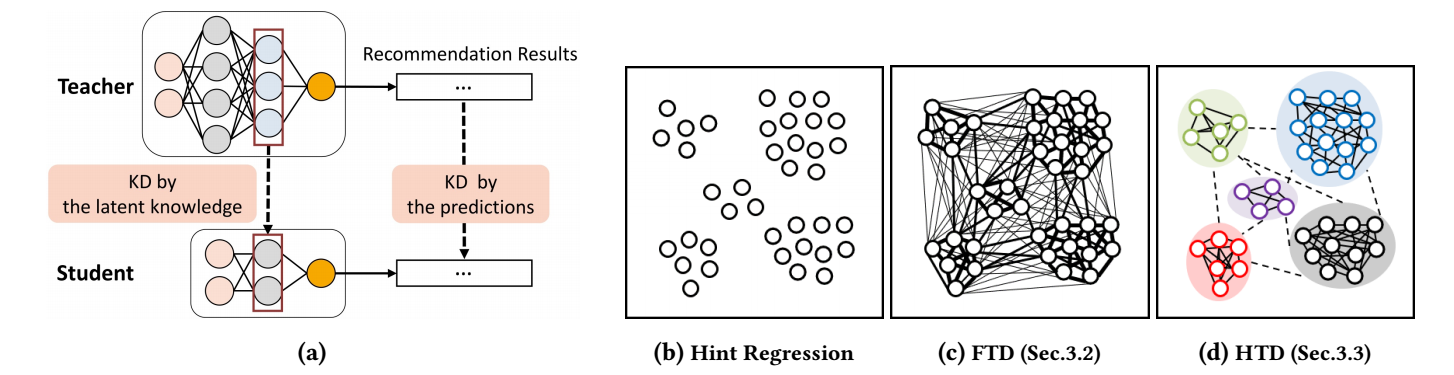
Full Topology Distillation (FTD)
-
对于一个 batch, FTD 首先计算教师模型中所对应的两两相似度:
\[a_{ij}^t = \rho (\mathbf{e}_i^t, \mathbf{e}_j^t), \]这里, 作者用 cosine similarity 来计算相似度 \(\rho(\cdot, \cdot)\). 对于一个 batch size 为 \(b\) 的情况, 可以得到
\[\mathbf{A}^t \in \mathbb{R}^{b \times b} \]的相似度矩阵.
-
类似的, 我们可以得到学生模型的相似度矩阵 \(\mathbf{A}^s\). 很自然地, 我们可以通过如下损失要求 \(\mathbf{A}^s\) 与 \(\mathbf{A}^t\) 保持一致:
\[\mathcal{L}_{FTD} = \|\mathbf{A}^s - \mathbf{A}^t\|_F^2. \]
Hierarchical Topology Distillation (HTD)
-
HTD 认为 FTD 的限制还是太强了, 希望首先将 embedding 分成 \(K\) 个 groups, 然后 groups 间和 group 内分别蒸馏.
-
分组的步骤, HTD 利用一个额外的小网络 \(v: \mathbb{R}^{d^t}: \rightarrow \mathbb{R}^K\), 然后得到 item \(i\) 的类别向量
\[\bm{\alpha}_i = v(\mathbf{e}_i^t) \in \mathbb{R}^K. \]即
\[\alpha_{ik} = P(z_{ik} = 1| v, \mathbf{e}_i^t). \] -
有了概率向量, HTD 采用 Gumbel-Softmax 来采样具体的类别:
\[z_{ik} = \frac{\exp((\alpha_{ik} + g_k) / \tau)}{\sum_{j=1}^K \exp((\alpha_{ij} + g_j)/ \tau)}, \quad g \sim \text{Gumbel}(0, 1). \]注: 上面的公式似乎是错的, \(\alpha\) 应该替换为 \(\ln \alpha\).
-
注: 读者可能觉得这分明就是一个连续的近似, 并不是离散的, 实际上 PyTorch 的 gumbel_softmax 实现中若令 hard=True 就会从该分布中采样, 并且可微 (通过某种技巧).
-
现在我们已经有了分配矩阵 \(\mathbf{Z} \in \{0, 1\}^{b \times K}\), \(z_{ik} = 1\) 若 item \(i\) 属于第 \(k\) 个 group.
-
现在, 我们可以根据这个分配矩阵来得到每个 group 中的 items, 并令这些 items 的 embedding 的平均作为类内中心, 即
\[\mathbf{P}^t = \tilde{\mathbf{Z}}^T \mathbf{E}^t, \quad \mathbf{P}^s = \tilde{\mathbf{Z}}^T \mathbf{E}^s, \]其中 \(\mathbf{E}^t, \mathbf{E}^s\) 为当前 batch 的 item embeddings. \(\tilde{\mathbf{Z}}\) 为 \(\mathbf{Z}\) 的按列平均后的矩阵.
-
类间距离: HTD 考虑两种类间距离,
- 一种是最直接的 group-group:\[h_{km} = \rho(\mathbf{P}_{k,:}, \mathbf{P}_{m,:}), \]由此可以得到 \(\mathbf{H}^t, \mathbf{H}^s \in \mathbb{R}^{K \times K}\).
- 另一种是 group-item:\[h_{kj} = \rho(\mathbf{P}_{k,:}, \mathbf{e}_j). \]由此可以得到 \(\mathbf{H}^t, \mathbf{H}^s \in \mathbb{R}^{K \times b}\).
- 一种是最直接的 group-group:
-
类内距离: 这个比较简单, 就是考虑每个 group 内的两两的相似度, 如果令
\[\mathbf{M} = \mathbf{Z}\mathbf{Z}^T, \]则这部分的蒸馏损失可以总结为:
\[\|\mathbf{M} \odot (\mathbf{A}^t - \mathbf{A}^s)\|_F^2. \] -
最后, 我们的 HTD 蒸馏损失为:
\[\mathcal{L}_{HTD} = \gamma(\|\mathbf{H}^t - \mathbf{H}^s\|_F^2 + \|\mathbf{M} \odot (\mathbf{A}^t - \mathbf{A}^s)\|_F^2) + (1 - \gamma) (\sum_{i=1}^b \|\mathbf{e}_i^t - \sum_{k=1}^K z_{ik} f_k(\mathbf{e}_i^s)\|_2^2), \]注意到, 后半部分是为了保证一个比较合理的分类效果.


