Learning Heterogeneous Temporal Patterns of User Preference for Timely Recommendation
概
本文探讨时序信息的利用, 既考虑了流行度的影响, 又考虑了个性化的因素.
符号说明
- \((u, i, t)\), (user, item, timestamp);
- \(U_u\), user embedding for \(u\);
- \(I_i\), item embedding for \(i\);
- \(E_{Month}(t)\), month embedding for \(t\)
TimelyRec
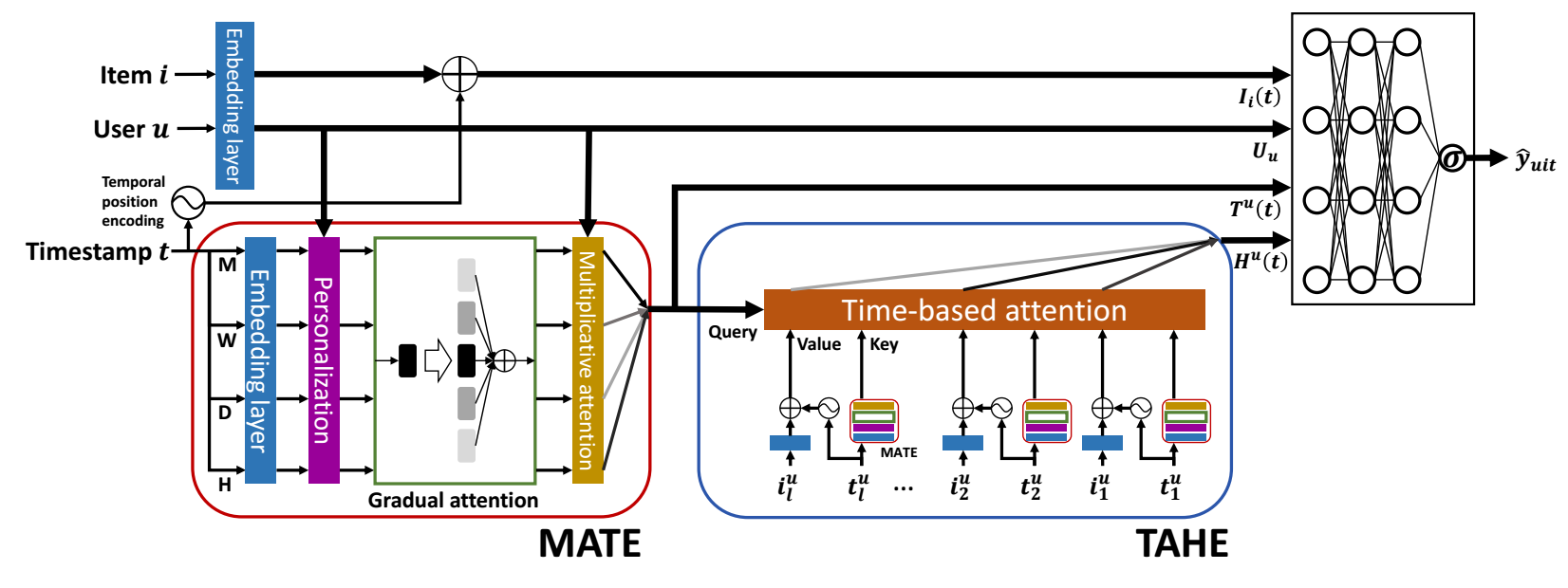
- TimelyRec 主要包括 MATE 和 TAHE 两个部分, 前者提取是时间相关的个性化 embedding, 后者主要针对历史交互序列.
Multi-aspect Time Encoder (MATE)
-
这部分我们以月份 (month) 为例来说明如何提取和月份信息相关且个性化的 embedding.
-
首先, 我们通过如下方式得到:
\[E_{Month}^u(t) = (W_{Month} U_u) \circ E_{Month}(t) \in \mathbb{R}^d, \]其包括 personalized period information. \(W_{Month} \in \mathbb{R}^{n \times n}\) 为可训练的权重矩阵.
-
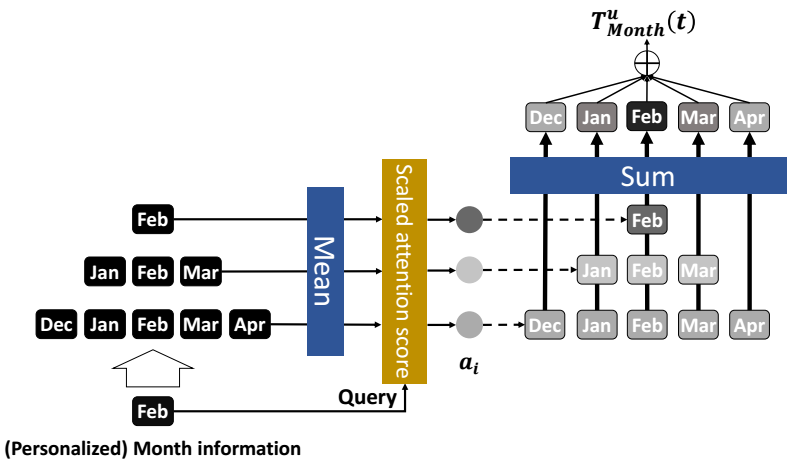
出了一些规律的周期性的 pattern 外 (比如流行度), 每个用户都会呈现出一些不规律的 pattern, MATE 通过把时间范围拓宽到 \(t\) 之外来捕获这些信息. 如下图所示:
-
具体地, 我们定义时刻 \(t\), 邻居范围 \(j\) 的 embedding 为:
\[T_{Month}^{'u}(t, j) = \left \{ \begin{array}{ll} E_{Month}^u(t) & j = 0 \\ \frac{\sum_{n=-j}^j E_{Month}^u (\Delta_{Month}(t, n))}{2j + 1} & j \not = 0. \end{array} \right . \] -
接着, 我们通过 attention 来重加权这些 embeddings:
\[a_i = \frac{\exp(E_{Month}^u(t) \cdot T_{Month}^{'u}(t, i)/ \sqrt{d})}{\sum_{i'=0}^{r_M} \exp(E_{Month}^u(t) \cdot T_{Month}^{'u}(t, i')/ \sqrt{d})}, \\ T_{Month}^u (t) = \sum_{i=0}^{r_M} a_i T_{Month}^{'u} (t, i). \] -
当然了, 除了月份, 我们还有 DayOfWeek, Date, Hour 等时间信息, 对于每个我们都可以类似地计算 embedding, 最后的 embedding 为:
\[C = \{Month,DayOfWeek,Date,Hour\} \\ b_i = \sigma(WU_u \cdot T_i^u(t)) \text{ for } i \in C \\ T^u(t) = \sum_{i \in C} b_i T_i^u (t). \]
Time-aware History Encoder (TAHE)
-
MATE 输出的 embedding 隐含了用户的个性化信息和当前时刻的时间信息, 接下来, 我们把用户的历史交互信息通过 TAHE 融入进来.
-
item embedding: 首先, 我们有 item embedding \(I_i\), 我们希望注入位置信息让模型知晓千欧关系, 这里通过常见的 sinusoidal positional encoding 来实现:
\[TE(t, j) = \left \{ \begin{array}{ll} \sin( \frac{t / 3600}{10000^{j / d}} ), & \text{ if } j \text{ is even} \\ \cos( \frac{t / 3600}{10000^{j / d}} ), & \text{ if } j \text{ is odd} \\ \end{array} \right ., \\ TE(t) = [TE(t, 0), TE(t, 1), \ldots, TE(t, d-1)]^T, \\ I_i(t) = I_i + \alpha TE(t) \in \mathbb{R}^d. \] -
现在我们有一串序列 \([(i_1, t_1^u), \ldots, (i_j, t_j^u), \ldots, (i_l, t_l^u)]\), TAHE 通过如下的方式编码:
\[H^u(t) = \sum_{j=1}^l c_j^u(t) I_{i_j^u}(t), \\ c_j^u(t) = \frac{\cos(T^u(t), T^u(t_j^u)) + 1}{2}. \]
Prediction
-
最后的预测融合 4 部分的属性:
\[x_{uit} = [U_u, I_i(t), T^u(t), H^u(t)], \]然后
\[\hat{y}_{uit} = \sigma(\text{MLP}(x_{uit})). \] -
通过 BCE 进行训练.
代码
[official]

