Graph transduction via alternating minimization
Wang J., Jebara T. and Chang S. Graph transduction via alternating minimization. ICML, 2008.
概
一种对类别不均更鲁棒的半监督算法.
符号说明
- \(\mathcal{X}_l = \{\mathbf{x}_1, \cdots, \mathbf{x}_l\}\), labeled inputs;
- \(\mathcal{X}_u = \{\mathbf{x}_{l+1}, \cdots, \mathbf{x}_{l+u}\}\), unlabeled inputs;
- \(\mathcal{X} = (\mathcal{X}_l, \mathcal{X}_u)\);
- \(\mathcal{L} = \{1, 2, \ldots, c\}\), 类别;
- \(\mathcal{G} = \{\mathcal{X}, \mathcal{E}\}\), 图;
- \(\mathbf{W} = \{w_{ij}\}\), weight matrix, \(w_{ij} = k(\mathbf{x}_i, \mathbf{x}_j)\);
- \(\mathbf{D} = \text{diag}([d_1, \cdots, d_n])\), degree matrix, \(d_i = \sum_{j=1}^n w_{ij}\);
- \(\mathbf{Y} \in \mathcal{B}^{n \times c}\), \(\mathbf{x}_i\) 若有 label \(y_i = j\), 则 \(Y_{ij} = 1\) 否则为 0;
- \(Y_{i\cdot}, Y_{\cdot j}\) 分别表示第 \(i\) 行和第 \(j\) 列;
- graph Laplacian:\[\mathbf{\Delta} = \mathbf{D - W}; \]
- normalized graph Laplacian:\[\mathbf{L} = \mathbf{D}^{-1/2}\mathbf{\Delta} \mathbf{D}^{-1/2}. \]
GTAM
-
现在的状况是, 我们仅有 \(\mathcal{X}_l\) 上的标签且很有可能是带有噪声的, 且不同类别的观测量也可能是不平衡的, 我们希望借此和图的结构 \(\mathbf{W}\) 来预测 \(\mathcal{X}_u\) 上的标签.
-
以往的方法往往采用最小化如下问题
\[\tag{1} \mathcal{Q}(\mathbf{F}) = \frac{1}{2}\Big( \underbrace{\sum_{i, j=1}^n w_{ij} \|\frac{\mathbf{F}_{i\cdot}}{\sqrt{\mathbf{D}_{ii}}} - \frac{\mathbf{F}_{j\cdot}}{\sqrt{\mathbf{D}_{jj}}}\|^2}_{Q_{smooth}} + \mu \underbrace{\sum_{i=1}^n \|\mathbf{F}_{i\cdot} - \mathbf{Y}_{i\cdot}\|^2}_{Q_{fit}}, \Big) \]得到 \(\mathbf{F}^*\), 然后每个结点的标签可以通过如下方式预测:
\[\hat{y}_i := \arg \max_j F_{ij}^*. \] -
细心的同学可以发现, 上面的方式可以独立拆分为:
\[\mathcal{Q}(\mathbf{F}) = \mathcal{Q}(\mathbf{F}_{\cdot 1}) +\mathcal{Q}(\mathbf{F}_{\cdot 2}) + \cdots +\mathcal{Q}(\mathbf{F}_{\cdot c}). \] -
既然对每个 label 这么独立的计算, 观测到更多数量的类别在最后的预测中往往会占据更强大的位置. 换言之, 最后的结果往往会偏向这些主要的类别.
-
GTAM 除了连续的分类矩阵 \(\mathbf{F} \in \mathcal{R}^{n \times c}\), 额外维护一个二元的标签矩阵 \(\mathbf{Y} \in \mathcal{B}^{n \times c}\), 然后优化问题转为:
\[\tag{2} \begin{array}{rl} \min_{\mathbf{F}, \mathbf{Y}} & \mathcal{Q}(\mathbf{F}, \mathbf{Y}) = \frac{1}{2}\text{tr}(\mathbf{F}^T \mathbf{LF} + \mu (\mathbf{F} - \mathbf{VY})^T (\mathbf{F} - \mathbf{VF})) \\ \text{s.t.} & \sum_{j} Y_{ij} = 1. \end{array} \]注: \(\mathbf{Y}\) 初始化为观测到的标签, 而且 GTAM 的算法中, \(\mathbf{Y}\) 的为 \(1\) 的元素是不会改变的, 所以可以认为已经观测到的元素是不需要训练的.
-
容易发现, 当 \(\mathbf{V} = \mathbf{I}\) 且 \(\mathbf{Y}\) 不可训练的时候, (2) 就退化成了 (1).
-
GTAM 令 \(\mathbf{V}\) 为一个对角矩阵 \(\mathbf{V} = \text{diag}(\mathbf{v})\), 其中
\[\mathbf{v} = \sum_{j=1}^c \frac{\mathbf{Y}_{\cdot j} \odot \mathbf{D} \mathbf{1}}{\mathbf{Y}_{\cdot j}^T \mathbf{D} \mathbf{1}}. \]容易发现, 此时每个类别的总权重都为 \(1\), 然后匀到各个样本点中去 (换言之, 对于数目众多的类别, 每个样本点分配的权重就会少一点). 若令
\[\mathbf{Z} := \mathbf{VY}, \]可以证明
\[\sum_{i} \mathbf{Z}_{ij} = 1. \] -
当然了, 我们也可以假定不同类别的总权重是不一致的, 这取决于我们的先验.
交替优化求解
-
Minimization for \(\mathbf{F}\): 当我们固定 \(\mathbf{Y}\) 的时候, 关于 \(\mathbf{F}\) 是一个凸函数, 可以直接得到它的显式解:
\[\mathbf{F}^* = \underbrace{(\mathbf{L} / \mu + \mathbf{I})^{-1}}_{=:\mathbf{P}} \mathbf{VY}. \] -
Greedy minimization of \(\mathbf{Y}\):, 将上面的解带入 (2) 可得:
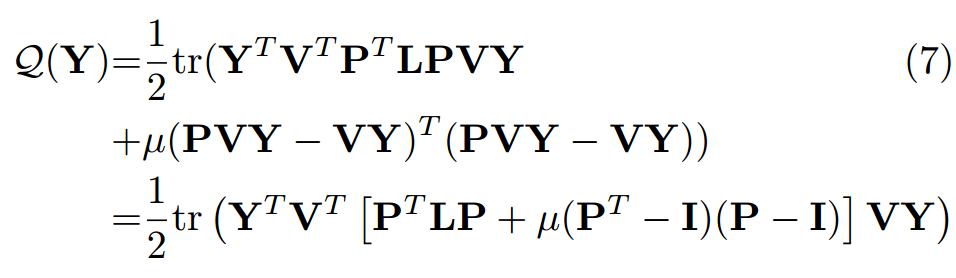
-
受限于 \(\mathbf{Y}\) 的二元约束, GTAM 采用贪心的方式逐步将 \(\mathbf{Y}\) 中非零的元素转换为 1.
-
主要思想是, 计算 \(\nabla \mathcal{Q}(\mathbf{Y})\) 的 largest negative gradient 是一个较为可靠的点.
-
注意到, 当我们用 \(\mathbf{Z}\) 替换, 可以得到更加简单的方式:
\[\mathcal{Q}(\mathbf{Z}) = \frac{1}{2} \text{tr}(\mathbf{Z}^T \mathbf{A} \mathbf{Z}), \]其中
\[\mathbf{A} = \mathbf{P}^T \mathbf{L} \mathbf{P} + (\mathbf{P}^T - \mathbf{I})(\mathbf{P} - \mathbf{I}). \] -
于是, 我们估计下一个标签为:
\[(i^*, j^*) = \text{argmin}_{\mathbf{x}_i \in \mathcal{X}_u, 1 \le j \le c} \nabla_{\mathbf{Z}_{ij}} \mathcal{Q}. \]并令
\[\mathbf{Y}_{i^*, j^*} = 1, \]其余元素不变. 重复上述的过程直到所有的结点都被打标.
-
注: 文中提到:
\[\arg\min_{i, j} \frac{\partial \mathcal{Q}}{\partial Y_{ij}} = \arg \min_{i,j} \frac{\partial \mathcal{Q}}{\partial Z_{ij}}, \]其实应该不是这么一回事. 因为
\[\nabla_Y \mathcal{Q} = \mathbf{V}^{-1} \nabla_Z \mathcal{Q}, \]所以对于每一个结点 \(\mathbf{x}_i\), 其中所应该被打标的点是不变的, 但是 \(\mathbf{x}_i, \mathbf{x}_j\) 的相对顺序是存在变化的.
-
最后, 总的流程为:
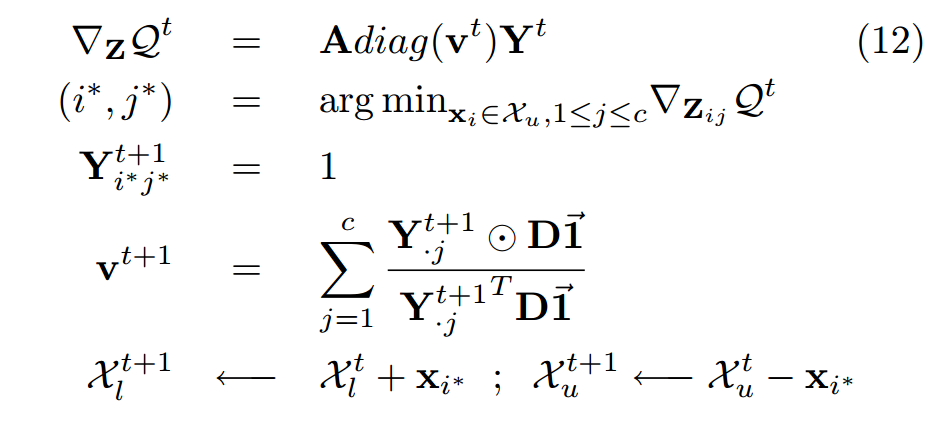
-
注意到, 实际上我们不需要显式计算 \(\mathbf{F}\), 上面的过程只是 \(\mathbf{Y}\) 不断更新而已.


