How Expressive are Graph Neural Networks in Recommendation
概
分析图的表达能力 (node-level, link-level), 然后提出了一种不用训练的推荐算法 (实际上就是一种计算两个结点间长度为 \(k\) 的路径数量的快速算法).
符号说明
-
\(\mathcal{N}(v)\), 结点 \(v\) 的一阶邻居;
-
\(\{\cdot\}\) multiset, 此类集合中的元素允许有多个同类元素, 此时
\[\{\cdot\}_1 = \{\cdot\}_2 \]这表明两个 set 具有相同种类的元素, 且每种元素的个数也是相同的.
-
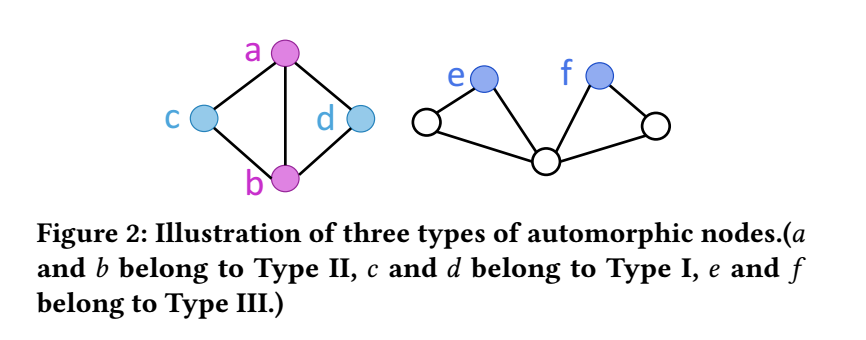
将自同构的结点分成如下三类:
- Type I: \((u, v)\) 为 Type I 的点若
\[\mathcal{N}(u) = \mathcal{N}(v). \]- Type II: \((u, v)\) 为 Type II 的点若
\[\mathcal{N}(u) - \{v\} = \mathcal{N}(v) - \{u\}. \]- Type III: \((u, v)\) 为 Type III 的点若
\[\mathcal{N}(u) - \{v\} \not= \mathcal{N}(v) - \{u\}. \] -
下图是三种类型的一个示意图:
- 一般的图网络都涉及 aggregation, 第 \(k\) 层的 aggregation 可以描述为:\[h_v^{(k)} = g(\{h_u^{k-1}: u \in \mathcal{N}(v) \cup \{v\}\}). \]
Node-level
-
Theorem2: 假设 aggregation \(g(\cdot)\) 是一单射且结点的初始 embedding 各不相同, 则第 \(k\) 层结点 \(u, v\) 的 embedding 也不同若:
- \(u, v\) 为 Type I or III 的结点且 aggregation 中有残差连接.
- \(u, v\) 为 Type II or III 的结点且 aggregation 中没有残差连接.
-
上面定理中的残差连接是指: 一般的没有残差连接的 aggregation 为:
\[h_v^{(k)} = g(\{h_u^{k-1}: u \in \mathcal{N}(v)\}), \]有残差连接的情况为:
\[h_v^{(k)} = g(\{h_u^{k-1}: u \in \mathcal{N}(v) \cup \{v\}\}). \] -
上面的定理证明很简单, 就是分析在不同的结构和结点类型下, \(g(\cdot)\) 的输入的差别.
-
Lemma3: 结点个数大于 2 的连通二部图不存在 Type II 类型的结点.
-
这个也很好证明, 画两笔图就明白了.
-
有了上面的理论, 我们很容易能够推得:
-
Theorem 4: 对于结点个数大于 2 的连通二部图, aggregation 机制带有残差连接, 则若初始 embedding 各不相同, 则每一次 aggregation 后的结点的 embedding 也各不相同.
-
显然, 成立的原因是此时 \((u, v)\) 只能是 Type I or III, 结合定理 2 便是显然的.
Topological Closeness
-
在推荐中, 仅仅区分不同的结点是不够的, 我们希望在结构上相似的结点最后的 embedding 也是相似的, 作者首先定义了结构相似性.
-
k-hop Topological Closeness: 对于无向图中的两个结点 \((u, v)\) 而言, 他们间的 \(k\)-hop topological closeness 定义为:
\[k-TC(u, v) = |\mathcal{P}_{u, v}^k|, \]其中 \(\mathcal{P}_{u, v}^k\) 是 \(u, v\) 间所有的长度为 \(k\) 的路径 (允许重复的点和边, self-loops).
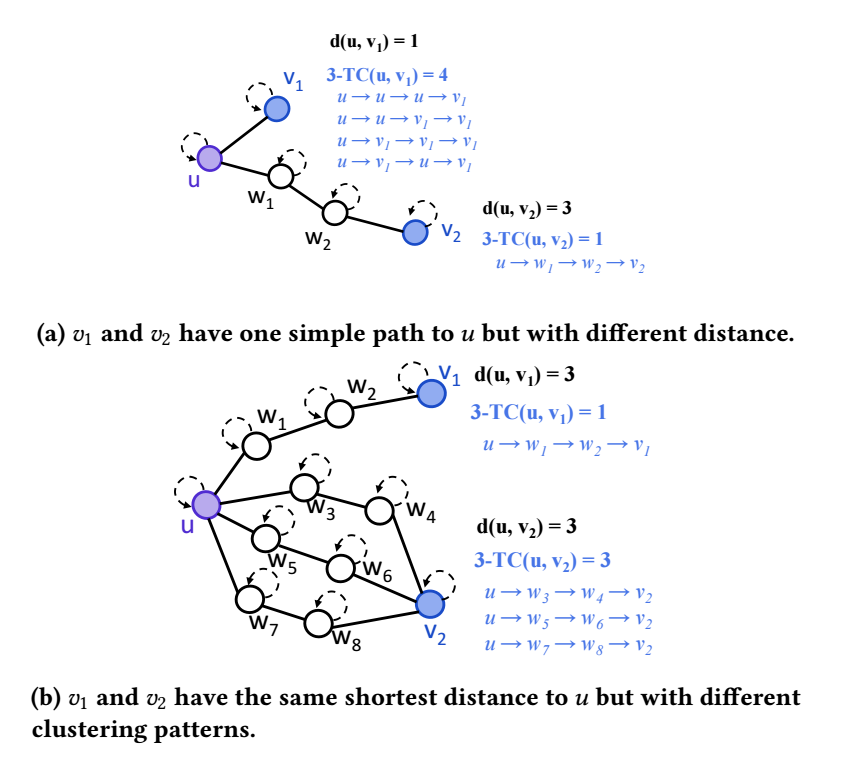
-
上图展示了两种不同的情况下的 \(3-TC\). 可以发现, 如果是采用最短路径 \(d(u, v)\) 来衡量两个结点间的相似度的话, (b) 的情况会得出一个反直觉的答案, 即 \(v_1, v_2\) 和 \(u\) 是同等近似的. 但是用 \(k\)-hop TC 则不存在这个问题.
-
接下来, 作者讨论在如下的 aggregation 机制下是否能够捕捉到 Topological closeness 的问题:
\[\mathbf{e}_u^(k) = \sum_{v \in \mathcal{N}_u} \mathbf{e}_v^{(k-1)} + \mathbf{e}_u^{(k-1)}, \mathbf{e}_v^(k) = \sum_{u \in \mathcal{N}_v} \mathbf{e}_u^{(k-1)} + \mathbf{e}_v^{(k-1)}. \]并采用如下方式计算 score:
\[\hat{y}_{u,v} = \mathbf{e}_u^{(L)} \cdot \mathbf{e}_v^{(L)}. \] -
倘若这种方式能够正确建模 Topological closeness, 则倘若 \(L-TC(u, v_1) > L-TC(u, v_2)\), 则应当满足
\[\hat{y}_{u, v_1} > \hat{y}_{u, v_2}. \]但是作者证明上面的机制并不能够保证这一点.
-
证明主要是通过如下的引理以及初始 embedding 毫无限制 (所以导致 \(\mathbf{e}_u^{(0)}\cdot \mathbf{e}_v^{(0)} 的大小是任意的\)):
-
Lemma 6: 上面的更新机制等价于:
\[\mathbf{e}_u^{(k)} = \sum_{w \in \mathcal{N}^k(u) \cup \{u\}} k-TC(u, w) \cdot \mathbf{e}_w^{(0)}. \]
GTE
-
作者引入 GTE, 它和前面的更新机制不同之处在于, embedding 的初始化:
\[\mathbf{e}_{v_i}[j] = \left \{ \begin{array}{ll} 1 & i = j \\ 0 & i \not = j \end{array} \right .. \in \mathbb{R}^{|\mathcal{I}|} \]这里 \(\mathcal{I}\) 表示 items 的集合. 而对于 user 的初始化为:
\[\mathbf{e}_{u} = \mathbf{0} \in \mathbb{R}^{|\mathcal{I}|}. \] -
如此一来, 可以证明,
\[\mathbf{e}_{w}^{(k)} [j] = k-TC(w, v_j). \] -
所以, 最后的输入就直接建模了 \(L-TC\), 自然就满足我们所希望的性质.
-
所以, 该算法实际上就是用 \(k\)-hop 来计算相似度, 只不过相比于我们一个一个来统计两个结点的路径长度, 这种方式更加方便快捷.
代码
[official]


