Time Matters Sequential Recommendation with Complex Temporal Information
概
Absolute + Relative 信息, 相对来说, 在 motivation 这一块挺详细的.
符号说明
- \(\mathcal{U}, \mathcal{I}\), users, items;
- \(S^u = [(s_1^u, t_1^u), (s_2^u, t_2^u), \ldots, (s_{l_u}^u, t_{l_u}^u)]\), \((s_i^u, t_i^u)\) 表示在时刻 \(t_i^u\) 所交互的 item.
TASER
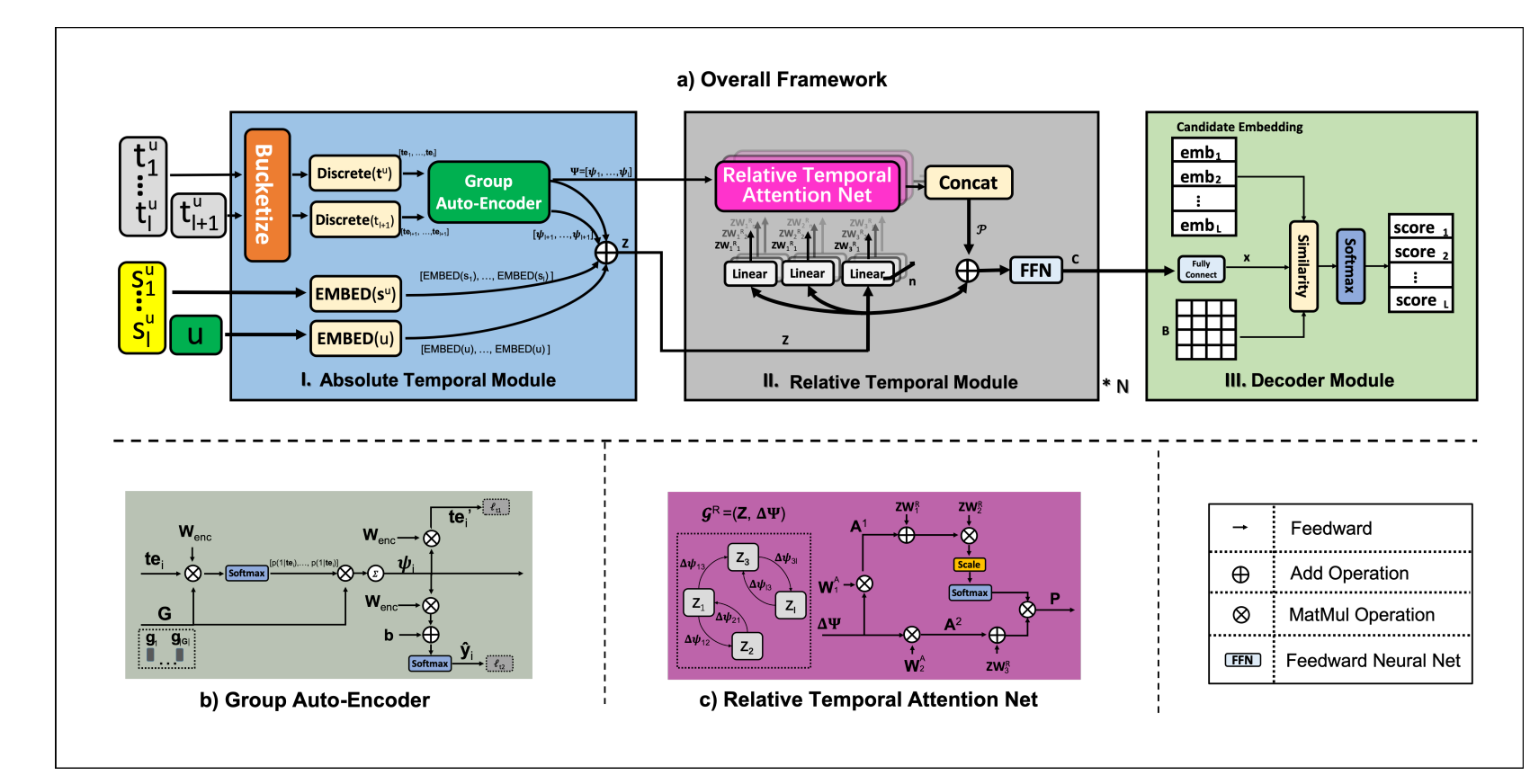
- TASER 的做法是首先通过 Absolute Temporal Modules 获得注入了绝对时间信息的 embedding, 然后再通过 Relative Temporal Module (主要是通过 attention) 注入相对时间信息. 最后通过一个 decoder 计算和不同 items 间的 scores.
Absolute Temporal Module
-
假设序列长度为 \(l\), 除了序列中的时间信息 \(\bm{t}^u = [t_1, t_2, \ldots, t_l]\), 该模块还需要下一时刻的时间信息 \(t_{l+1}\), 然后该模块的输出为:
\[\bm{z}_i = \mathrm{E}(u) + \mathrm{E}(s_i^u) + \mathrm{E}(t_i^u) + \mathrm{E}(t_{l+1}^u), \]\(\mathrm{E}(\cdot)\) 为 embedding layer.
-
对于 user \(u\) 和 item \(s_i^u\), 就是普通的 embedding layer.
-
对于每个时间戳, 是这么做的, 首先通过分桶将时间戳离散化, 接着我们可以得到:
\[\bm{\tau}_i = \mathrm{E}(t_i) = \mathrm{E}(Bucketize(t_i)) \in \mathbb{R}^d. \] -
接着我们通过一个 group encoder 来进行转换. 该 encoder 有 \(|G|\) 个 groups:
\[\bm{G} = \{\bm{g}_1, \bm{g}_2, \ldots, \bm{g}_{|\bm{G}|}\}. \]接着
\[\bm{\psi} := \sum_{j=1}^{|\bm{G}|} p(j|\bm{\tau}) \bm{g}_j, \\ p(j|\bm{\tau}) = \frac{\exp(\bm{\tau}^T \bm{W}_{enc} \bm{g}_j)}{\sum_{k \in |\bm{G}|} \exp(\bm{\tau}^T \bm{W}_{enc} \bm{g}_k)}. \] -
故, 这部分的 embedding 实际上为:
\[\bm{z}_i = \mathrm{E}(u) + \mathrm{E}(s_i^u) + \mathrm{E}(t_i^u) + \bm{\psi}_i + \bm{\psi}_{l+1}. \]
Relative Temporal Module
-
这部分实际上就和相对位置编码类似了, 首先在计算 attention map \(\bm{E} \in \mathbb{R}^{l \times l}\) 的时候, 系数的计算方式改为:
\[e_{ij} = \frac{ (\bm{z}_i \bm{W}_1^R) (\bm{z}_j \bm{W}_2^R + (\bm{\psi}_i - \bm{\psi}_j) \bm{W}_1^A)^T }{\sqrt{|\bm{z}_i \bm{W}_1^R|}}. \] -
然后变换后的特征为:
\[\bm{p}_i = \sum_{j=1}^l e_{ij}(\bm{z}_j \bm{W}_3^R + (\bm{\psi}_i - \bm{\psi}_j) \bm{W}_2^A). \] -
可以类似地推广到多头注意力机制.
-
然后通过 FFN 得到:
\[\bm{C} = \text{FFN}(\bm{Z} + \bm{\mathcal{P}}) \in \mathbb{R}^{l \times d}. \]
Decoder
-
这部分就是首先利用一个线形层:
\[\bm{x} = linear(\bm{C}) \in \mathbb{R}^d. \] -
然后通过与 item embeddings 的内积计算 scores:
\[score_i = \bm{e}_i^T \mathbf{B} \bm{x}, \]虽然作者实际上额外引入了一个可训练的矩阵 \(\mathbf{B}\).


