A Contextualized Temporal Attention Mechanism for Sequential Recommendation
概
考虑 temporal 信息的序列推荐.
符号说明
- \(\mathcal{V}\), items, \(|\mathcal{V}| = N\);
- \(\mathcal{U}\), users, \(|\mathcal{U}| = U\);
- \(\mathcal{S}^u = \{(t_1^u, v_1^u), (t_2^u, v_2^u), \ldots\}\), 用户 \(u\) 的交互序列, \(t, v\) 分别为时间戳和 item;
CTA
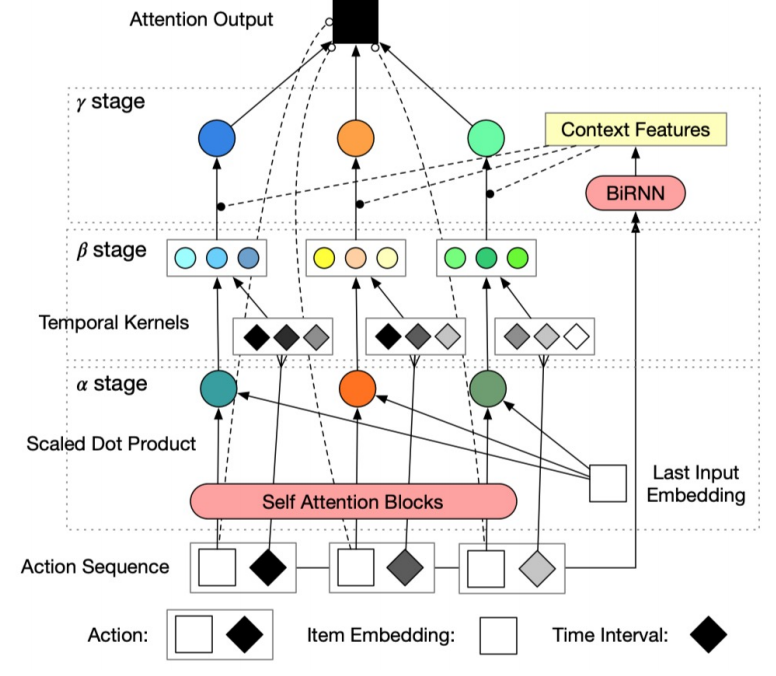
作者给了一个图, 不过说实话, 这个图真是越看越迷糊:
-
总的来说, 作者的模型总共分为三个阶段, \(\alpha, \beta\) stages 分别提取序列和时间信息, 最后的 \(\gamma\) stage 算是二者的一个融合.
-
首先, 我们限定序列的最大长度为 \(L\), 即我们只有:
\[\{(t_i, v_i\}_{i=1}^L. \] -
对于序列的 items, 我们将其转换为 embeddings (就是通过最简单的 look up): \(\bm{X} \in \mathbb{R}^{L \times d_{in}}\), 然后将时间戳转换为:
\[\bm{T} = [t_{L+1} - t_1, \ldots, t_{L+1} - t_L] \in \mathbb{R}^{L \times 1}, \]其中 \(t_{L+1}\) 为当前时刻. 实际上 \(\bm{T}\) 是 time span 的信息.
-
问: 我怎么知道用户会在哪个时候产生交互行为?
\(\alpha\) stage
-
这个 stage 是希望计算序列 \([v_1, \ldots, v_L]\) 中不同交互的重要性差异, 其主要通过 attention 计算.
-
首先, 利用一般的 multi-head attention + FFN + LN 的组合得到隐变量 \(\bm{H} \in \mathbb{R}^{L \times d_{in}}\).
-
不似一般的 Transformer 的架构直接用这个隐变量做预测, 利用
\[\bm{\alpha} = \text{softmax}(\frac{(\bm{H} W_0^Q) \cdot (\bm{x}_L W_0^K)^T}{\sqrt{d_{in}}}) \in \mathbb{R}^{L \times 1} \]来计算隐变量和 last item 的embedding \(\bm{x}_L\) 之间的相似度. \(W_0^Q, W_0^K \in \mathbb{R}^{d_{in} \times d_{in}}\) 为可训练的参数.
\(\beta\) stage
-
该 stage 希望对 time span 进行一定的转换, 并得到更好的时序信息.
-
不同的用户往往有着不同的行为模式, 所以对于 time span 的转换应当考虑到这一点, 故作者提出了多种 kernel functions:
- \(\phi(\bm{T}) = a e^{-\bm{T}} + b\), 指数衰减 kernel;
- \(\phi(\bm{T}) = -a \log (1 + \bm{T}) + b\), 对数衰减 kernel;
- \(\phi(\bm{T}) = -a \bm{T} + b\), 线性衰减 kernel;
- \(\phi(\bm{T}) = \bm{1}\) , 常数 kernel.
-
注意到设定不同的 \(a, b \in \mathbb{R}\), 每个 kernel 也会有所不同, 假设我们设定了 \(K\) 个不同的 kernels: \(\{\phi_1, \phi_2, \ldots, \phi_K\}\), 通过这些 kernels 我们得到:
\[\bm{\beta} = [\phi_1(\bm{T}), \ldots, \phi_K(\bm{T}))] \in \mathbb{R}^{L \times K}. \]
\(\gamma\) stage
-
该 stage 对两个信息进行一个融合, 主要是希望计算对每一个交互的一个权重.
-
作者通过 Bidirectional RNN 计算:
\[\bm{C} = \text{Bi-RNN}(\bm{X}) \oplus C_{attr} \in \mathbb{R}^{L \times d_r}, \]其中 \(C_{attr}\) 表示某些具体的属性, 但是实际上在本文中, 作者没有考虑这一点.
-
接下来:
\[\bm{\gamma} = \text{softmax}(\bm{\alpha} \odot \bm{\beta}^c) \in \mathbb{R}^{L \times 1}, \\ \bm{\beta}^c = \bm{\beta} \cdot \bm{p} \in \mathbb{R}^{L \times 1}, \\ \bm{p} = \text{softmax}(F^{\gamma} (\bm{C})) \in \mathbb{R}^{K \times 1}, \]其中 \(F^{\gamma}\) 是一个 feed-forward layer.
代码
[official]
