HS-GCN Hamming Spatial Graph Convolutional Networks for Recommendation
概
二值化的 node embedding.
符号说明
- \(\mathcal{U}\), users;
- \(\mathcal{I}\), items;
- \(\mathcal{V} = \mathcal{U \cup I}\), nodes;
- \(\mathcal{G} = (\mathcal{V}, \mathcal{E})\), graph;
- \(\mathbf{h}_u \in \{+1, -1\}^{K}\), user embedding;
- \(\mathbf{h}_i \in \{+1, -1\}^{K}\), item embedding;
- \(\text{sim}(u, i) = \frac{1}{K} \sum_{k=1}^K \mathbb{I} (h_{uk} = h_{ik})\), Hamming similarity;
HS-GCN
Initial Layer
-
为了能够训练, 在实际中, 我们会利用两个 proxy \(\mathbf{e}_u, \mathbf{e}_i\) 来实际建模, 并令
\[\mathbf{h}_u = \lim_{\beta \rightarrow \infty} \text{tanh}(\beta \mathbf{e}_u), \mathbf{h}_i = \lim_{\beta \rightarrow \infty} \text{tanh}(\beta \mathbf{e}_i). \] -
下面我们用 \(\mathbf{h}^{(0)}\) 表示这类初始化, 并用 \(\mathbf{h}^{(l)}\) 表示第 l 层的输出.
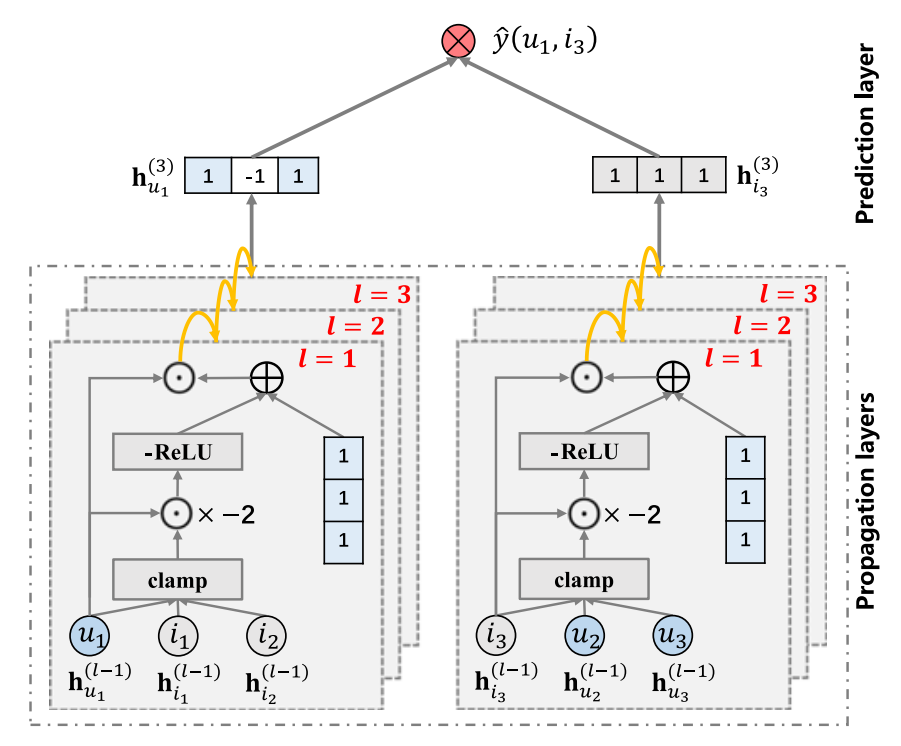
Propagation Layer
-
HS-GCN 希望利用 Propagation Layer 来聚合邻居的信息, 具体的:
\[\mathbf{m}_u^{(l)} = \text{clamp}(\mathbf{x}) = \left \{ \begin{array}{ll} 1, & \text{if } \mathbf{x} > 1, \\ \mathbf{x}, & \text{if } -1 \le \mathbf{x} \le 1, \\ -1, & \text{if } \mathbf{x} < -1. \end{array} \right., \]其中 \(\mathbf{x} = \mathbf{h}_u^{(l)} + \sum_{i \in \mathcal{N}_u} \mathbf{h}_i^{(l)}\).
-
显然 \(\mathbf{m}_u^{(l)} \in \{-1, 0, 1\}^K\).
Hash Code Encoding
-
获得 \(l+1\) 层的输出, HS-GCN 通过:
\[\mathbf{h}_u^{(l+1)} = \mathbf{c}_u^{(l)} \odot \mathbf{h}_u^{(l)} \\ \mathbf{c}_u^{(l)} = - \text{ReLU}(-2 \times \mathbf{d}_u^{(l)}) + \mathbf{1}, \\ \mathbf{d}_u^{(l)} = \mathbf{h}_u^{(l)} \odot \mathbf{m}_u^{(l)}. \] -
我们注意到, \(\mathbf{d}_u^{(l)} \in \{-1, 0, 1\}^K\), 其中 \(-1\) 表示当前的结点表示 \(\mathbf{h}_u^{(l)}\) 和邻居的结点在某个位置上很不相似, 而 \(1\) 则表示和绝大部分结点的方向是一致的.
-
\(\mathbf{c}_u^{(l)}\) 则是进一步考虑 \(0\) 的情况, 它实际上是将 \(0\) 纳入 \(-1\) 的范围.
矩阵表示
- 上述的过程可以用如下的矩阵表示:\[\mathbf{H}^{(l+1)} - \text{ReLU}(-2 \times \text{clamp}((\mathbf{A} + \mathbf{I}) \mathbf{H}^{(l)}) \odot \mathbf{H}^{(l)}) + \mathbf{1} \mathbf{1}^T. \]其中\[\mathbf{A} = \left [ \begin{array}{cc} \mathbf{0} & \mathbf{R} \\ \mathbf{R} & \mathbf{0} \end{array} \right ]. \]
Prediction Layer
- HS-GCN 用最后一层的输出作为最后的 embedding\[\mathbf{h}_u^* = \mathbf{h}_u^{(L)}, \mathbf{h}_i^* = \mathbf{h}_i^{(L)}, \]然后\[\hat{y}_{ui} = {\mathbf{h}_u^*}^T \mathbf{h}_i^*. \]
Optimization
-
HS-GCN 采用如下的损失训练:
\[\mathcal{L} = \mathcal{L}_{cross} + \lambda_1 \mathcal{L}_{rank}. \] -
其中
\[\mathcal{L}_{cross} = -\sum_{r_{ui} \in \mathbb{R}} r_{ui} \log (\sigma(\hat{y}_{ui})) + (1 - r_{ui}) \log (1 - \sigma(\hat{y}_{ui})) \]为 BCE 损失.
-
另外
\[\mathcal{L}_{rank} = \sum_{(u, i, j) \in \mathcal{D}} \max (0, -\sigma(\hat{y}_{ui}) + \sigma(\hat{y}_{uj}) + \alpha), \]其中 \(\mathcal{D} = \{(u, i, j)| (u, i) \in \mathcal{R}^+, (u, j) \in \mathcal{R}^-\}\). \(\mathcal{R}^+, \mathcal{R}^-\) 分别表示 observed 和 unobserved interactions, \(\alpha\) 表示 margin.
代码
[official]


