Query2box Reasoning over Knowledge Graphs in Vector Space using Box Embeddings
概
Box embedding 用于查询判断, 和我想的那个有很大差别啊. 我对这方面不是很了解, 只能记录个大概.
符号说明
-
, 知识图谱;
-
, entity;
-
, 为某种关系, 是一个二元函数:
满足 .
-
Conjunctive queries 定义为:
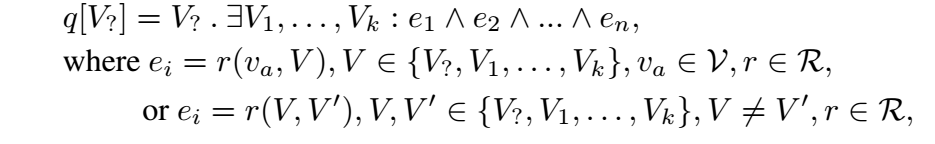
其中 是锚点, 是某些变量, 是目标变量.
-
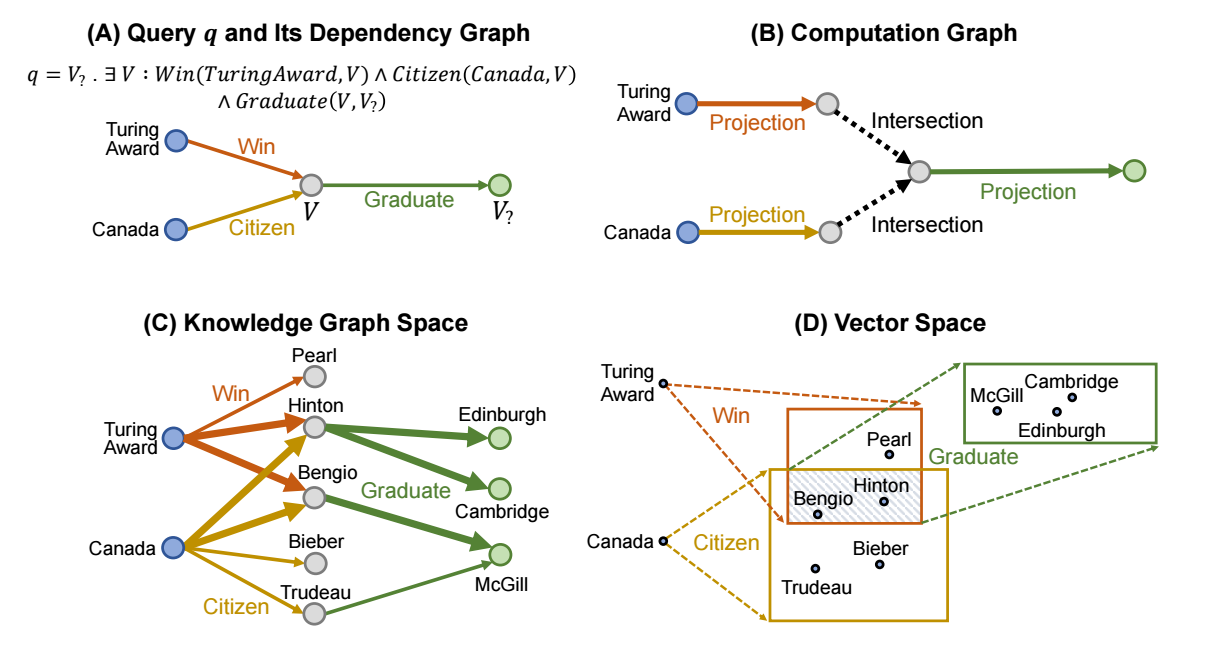
举个例子: "Where did Canadian citizens with Turing Award graduate?" 的查询中:
- [Truing Award], [Canada] 是锚点, 是起始变量;
- 这里只有一个(潜在)变量 [V], 它代表一些具体的人物: Pearl, Hinton, Bengio, Bieber, Trudeau;
- 目标变量 [V?] 是满足询问的回答, 即获得图灵奖且受奖于加拿大的大佬的毕业院校:
- Hinton: Edinburgh; Cambridge;
- Bengio: McGill.
-
我们用 来表示答案的集合 (称为 denotation set 或 answer set), 它满足:
Query2Box
-
Box embeddings 定义为二元组 , 前者表示 box 的中心, 后者为 positive offset. 由此, 它定义了如下的 box:
-
首先, 我们来看如何使用这个工具来进行 Conjunctive queries.
-
Conjunctive queries 中包含 这两个操作. 实际上等价于需要定义 Projection 和 Intersection 操作.
-
对于输入 , 和关系 box embedding , 定义投影为:
可以看成是 经过关系 转换后得到下一阶段的变量 (它应当被理解成为那些和 有紧密 关系的向量表示 (当然无法完全一致)).
-
假设我们有了一堆可能的 box embeddings , 我们需要找到一个尽可能满足 (即接近) 所有这些 box embeddings 的中心点
具体定义为:
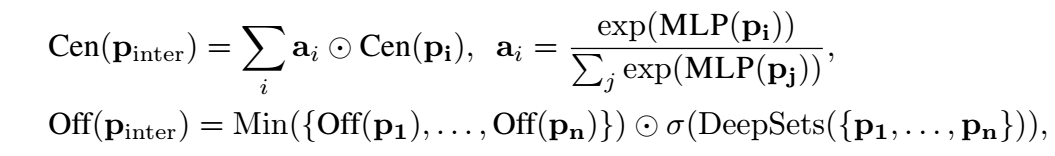
其中 -
现在我们已经定义了 Projection, 他实现了关系转移, Interaction, 它实现了交的操作, 现在还需要实现一个给定 去找到相匹配的 entity (检索) 的操作:
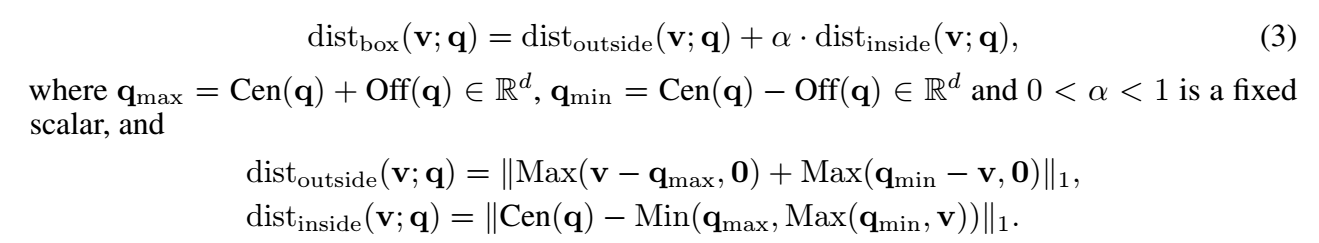
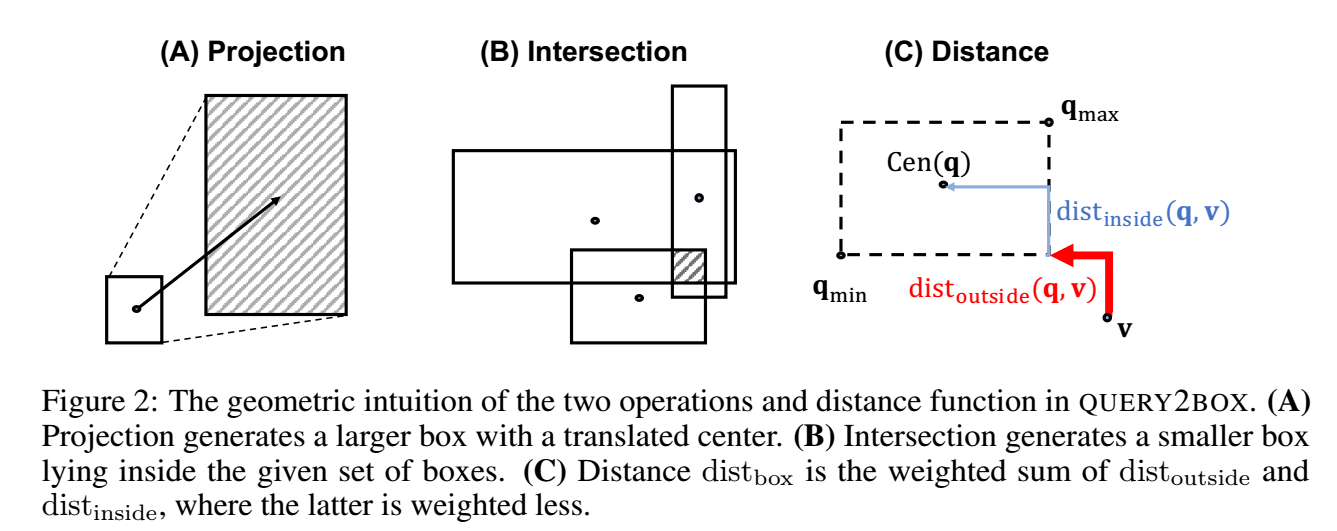
-
如上图 (C) 所示: 实际上是 到 边缘的最短(街区)距离, 当然, 倘若 在 Box 的内部, 概距离为 . 类似地, 刻画的是 到对应边缘的距离, 倘若 在内部, 实际上就是 到 的街区距离.
-
当 的时候, 整个距离退化为 .
-
训练, 采用如下损失
其中 为人为给定的 margin, 为正样本, 为负样本. 该损失是很直接的.
-
上面的操作综合下来看就是这样的:
- 给定一些锚点, 初始化为 ;
- 让后锚点通过 Projection 状态转移;
- 多个锚点发生 Interaction 操作;
- 如有必要重复 2, 3.
- 最后得到一个 , 然后通过 来检索相似的.
-
但是我怀疑这种状态转移和 Interaction 的操作是不是会丢失掉太多的信息?
代码
[official]




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
2022-07-14 Towards Long-term Fairness in Recommendation
2020-07-14 A New Defense Against Adversarial Images: Turning a Weakness into a Strength
2019-07-14 threading